Трехмерное вращение вокруг осей координат

 

При вращении вокруг оси х размеры вдоль оси х не изменяются, тогда матрица преобразования, соответствующая повороту на угол θ, имеет вид (вращение положительное):

 

.

 

При вращении на угол φ вокруг оси у матрица преобразования определяется выражением:

.

 

Аналогично матрица преобразования для вращения на угол ψ вокруг оси z имеет вид:

.

 

Следует отметить, что трехмерные вращения некоммутативны, т. е. порядок умножения матриц влияет на конечный результат, а значит вращение вокруг оси х, за которым следует вращение вокруг оси у, и вращение вокруг оси у и следующее за ним вращение вокруг оси х дают разные результаты.

 

Поворот вокруг оси, параллельной координатной оси

 

Если необходимо вращать объект вокруг оси, не совпадающей с координатными осями x, y, z, то требуется выполнить следующие процедуры (рис. 4.18):

1) переместить тело х (заданное в локальной системе x′, y′, z′) так, чтобы локальная ось совпала с координатной (координаты центра параллелепипеда х равны [х_о, у_о, z_о]);

2) повернуть вокруг указанной оси;

3) переместить преобразованное тело х^* в исходное положение.

Математически это записывается так:

 

 

где 1) [х^*] – преобразованное тело;

2) [х] – исходное тело;

3) [Т_r] – матрица перемещения  (сдвигает тело [х] параллельно плоскости х = 0 до тех пор, пока ось х’ не совпадет с осью х);

4) [R_x] – соответствующая матрица поворота  (выполняет требуемое вращение вокруг оси х);

5) [Т_r]^-1 – матрица, обратная матрице перемещения  (переносит ось х′, а следовательно, и повернутое тело [х] обратно в исходное положение).

 

Рис. 4.18

 

Чтобы совершить несколько поворотов в локальной системе осей х′, у′, z′, параллельных осям х, у, z, необходимо:

1) переместить локальную систему так, чтобы начало координат её совпало с началом координатных осей х, у, z;

2) выполнить требуемые повороты;

3) переместить локальную систему осей обратно в исходное положение.

Поворот вокруг произвольной оси в пространстве

 

Обобщенный случай поворота вокруг произвольной оси в пространстве встречается часто, например в робототехнике, мультипликации, моделировании. Следуя логике предыдущего обсуждения, поворот вокруг произвольной оси в пространстве выполняют с помощью переноса и простых поворотов вокруг координатных осей. Так как метод поворота вокруг координатной оси известен, то основная идея заключается в том, чтобы совместить произвольную ось вращения с одной из координатных осей.

Предположим, что произвольная ось в пространстве проходит через точку (х_о, у_о, z_о) с направляющим вектором (с_х, с_у, с_z). Поворот вокруг этой оси на некоторый угол δ осуществляется по следующему правилу: выполнить перенос так, чтобы точка (х_о, у_о, z_о) находилась в начале системы координат; соответствующие повороты так, чтобы ось вращения совпала с соответствующей осью, например, z; поворот на угол δ вокруг оси z; преобразование, обратное тому, что позволило совместить ось вращения с осью z; обратный перенос.

В общем случае для того, чтобы произвольная ось, проходящая через начало координат, совпала с одной из координатных осей, необходимо сделать два последовательных поворота вокруг двух других координатных осей. Для совмещения произвольной оси вращения с осью z сначала выполним поворот вокруг оси х, а затем вокруг оси у. Чтобы определить угол поворота α вокруг оси х, используемый для перевода произвольной оси в плоскость хz, спроецируем сначала на плоскость yz направляющий единичный вектор этой оси. Компоненты у и z спроецированного вектора равны с_у- и с_z-компонентам единичного направляющего вектора оси вращения.

Объединенное преобразование имеет вид:

 

,                   (4.64)

 

,

 

где j и θобозначают углы поворотов вокруг осей у′ и х′ соответственно.

Отражение в пространстве

 

Иногда требуется выполнить зеркальное отражение трехмерного объекта. В этом случае наиболее просто отражать относительно координатной плоскости. Для отражения с изменением масштаба необходимо, чтобы определитель преобразования был равен – 1,0.

Матрицы преобразования относительно плоскостей соответственно ху, уz, и хz следующие:

 

, , .

 

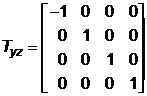Отражение относительно других плоскостей можно получить путем комбинации вращения и отображения.

Трехмерный линейный перенос изображения определяется выражением:

 .              (4.65)

 

Отражение относительно произвольной плоскости выполняется с помощью процедуры, объединяющей ранее определенные простые преобразования.

Тогда общее преобразование описывается матрицей

 

,                (4.66)

 

где матрицы [T], [R_x], [R_y] задаются уравнениями соответственно;
Rflt_z – матрица отражения относительно плоскости z = 0; (x_o, y_o, z_o) =
=(Р_х, Р_у, Р_z) – координаты точки Р на плоскости отражения; а (с_х, с_у, c_z) есть вектор нормали к плоскости отражения.

 

---

Дата добавления: 2018-04-04; просмотров: 3430; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!