Плоские и пространственные кривые. Поверхности

⇐ ПредыдущаяСтр 15 из 17Следующая ⇒

Существует много способов построения кривых вручную с помощью карандаша, ручки, кисточки, ножа и разнообразных инструментов: линейки, лекала, циркуля, плаза, шаблона и т. д. Каждый инструмент служит определенной цели, причем нет ни одного абсолютно универсального. Точно так же в машинной графике кривые строятся с помощью разных методов и инструментов. В этом разделе рассматриваются методы построения двумерных кривых, т. е. полностью лежащих в одной плоскости. Здесь ограничимся коническими сечениями.

Трехмерные, или пространственные, кривые широко используются в проектировании и разработке самой различной продукции: автомобилей, кораблей, самолетов, обуви, бутылок, зданий и т. д. Также они имеют большое значение для описания и интерпретации физических явлений в геологии, физике и медицине.

До начала применения математических и компьютерных моделей в процессе производства, дизайна и изготовления использовалась начертательная геометрия. Многие ее методы были перенесены в машинную графику.

Поверхности часто изображаются как сеть кривых, лежащих в ортогональных секущих плоскостях, с трехмерными контурами деталей. В этом случае сечения получают оцифровкой физической модели или чертежа и математическим подбором кривой, проходящей через все заданные точки.

Чаще всего рассматриваются два таких метода: кубических сплайнов и параболической интерполяции. Существуют и другие реализации этого подхода, например, математическое описание кривых генерируется без изначального знания формы кривой. Его примеры – это кривые Безье и их обобщение до В-сплайнов. Эти методы отличаются тем, что кривая может не проходить ни через одну заданную точку. Контрольные точки определяют только направление изгиба. Оба подхода можно применить при любом способе задания кривой.

Поверхности и их описание играют важную роль в конструировании и производстве. Очевидными примерами этого являются разработка и производство автомобильных кузовов, корабельных корпусов, авиационных фюзеляжей и крыльев, пропеллеров, турбин, компрессоров и лопастей вентиляторов; посуды, мебели и обуви. В этом случае сущность конструирования либо по функциональным, либо по эстетическим причинам составляет форма или геометрия поверхности. Описание поверхности также играет важную роль в представлении данных, полученных в медицине, геологии, физике и других естественных науках.

Традиционным способом представления поверхности является использование нескольких ортогональных проекций. По существу, поверхность задаётся сеткой ортогональных плоских кривых, лежащих на секущих плоскостях, и несколькими ортогональными проекциями определенных «характерных» пространственных линий (рис. 4.19). Эти кривые первоначально могут быть созданы на бумаге либо взяты (оцифрованы) из трехмерной модели, например в автомобильной промышленности дизайнерами традиционно используется глиняная модель.

а б

Рис. 4.19

В машинной графике и автоматизированном проектировании выгодно разрабатывать «настоящую» трехмерную математическую модель поверхности. Такая модель позволяет на ранних стадиях и относительно легко провести анализ характеристик поверхности, например кривизны, или физических количественных характеристик, зависящих от поверхности, например объекта, площади поверхности, момента инерции и т. д. Упрощается визуализация поверхности, применяемая для разработки или контроля за ходом разработки. Далее, по сравнению с традиционным методом, используют сетку линий, также существенно упрощается генерация необходимой для изготовления поверхности информации, например управляющих программ для станка с числовым программным управлением. Разработанные в последнее время методы описания поверхностей достигли такой стадии развития, что позволяют «почти» исключить традиционное описание поверхности с помощью сетки линий.

Существуют две основные идеи, лежащие в основе методов описания поверхностей. В первой, связанной в основном с именем Кунса, математическую поверхность стараются создать по заранее известным данным. Во второй, связанной в основном с имением Безье, математическую поверхность стараются создать ab initio (с самого начала). В первое время виды деятельности, связанные с числовыми параметрами, например конструирование, тяготели к первому подходу, тогда как другие, учитывающие визуальные, осязательные и эстетические факторы, например дизайн и живопись, тяготели ко второму.

Представление плоских кривых

В предыдущих подразделах изучались преобразования точек. Кривая может быть представлена совокупностью точек. Если точки расположены близко друг от друга, то, соединяя их отрезками прямой, можно получить изображение кривой. На рис. 4.19 показаны два разных точечных представления одной кривой. Точки на кривой рис. 4.19, а расположены равномерно по ее длине. В результате получается довольно плохое представление кривой, особенно, если мал радиус кривизны. Улучшить вид можно, увеличивая плотность точек в таких участках (рис. 4.19, б).

Хотя, как показано выше, кривые могут быть достаточно хорошо представлены совокупностью точек, аналитическое представление во многих отношениях предпочтительнее. Его преимущество – это точность, компактность записи и простота вычисления промежуточных точек. Аналитическое представление позволяет без труда определить наклон и радиус кривизны, а при точечном представлении для этого требуется численное дифференцирование – чрезвычайно неточная процедура. Сравните объем памяти для точечного представления окружности с 32 точками на ней и аналитическое представление – координаты центра и радиус. При аналитическом представлении кривой можно точно определить положение любой точки, а при точечном нужна интерполяция, причем в общем случае результат интерполяции не принадлежит кривой.

Опыт показывает, что аналитически представленные кривые легче изобразить на рисунке. Аналитическое представление выгоднее, когда для удовлетворения заданному критерию необходимо непрерывно изменять форму кривой. Ниже рассматриваются различные методы аналитического представления двумерных кривых.

Часто требуется аналитическое представление кривой, первоначально заданной точками. С математической точки зрения это проблема интерполяции. Для того чтобы провести кривую через все заданные точки, применяется метод кусочной полиномиальной аппроксимации. Для этого требуется определить коэффициенты полинома некоторой степени. Вид кривой в промежуточных точках зависит от степени полинома и граничных условий.

Если же точки – только приблизительные значения величин, например данные экспериментальных измерений или наблюдений, то нужна кривая, задающая верное направление изменения. В общем случае кривая может не проходить ни через одну точку данных. Здесь применяется метод наименьших квадратов. Метод наименьших квадратов дает кривую в виде y = f(x), которая минимизирует сумму квадратов отклонений по оси у между данными и полученной кривой. Вид y = f(x) выбирают исходя из характера изучаемого процесса.

Обычно для метода наименьших квадратов используются полиномы, степенные и экспоненциальные функции:

y = ax^b, y = ae^bx или y = c1+ c2x+c3x²+…+c_n+1 xⁿ,

где a, b и c_j – константы. Независимо от выбора вида кривой метод требует решения системы линейных алгебраических уравнений для определения неизвестных констант.

Непараметрические кривые

Математически кривая может быть представлена в параметрической или непараметрической форме. Непараметрическая кривая задается в виде явной или неявной функции. Для плоской кривой явное непараметрическое представление имеет вид:

Пример – уравнение прямой y = mx + b. При этом одному значению х соответствует только одно значение у, поэтому замкнутые или многозначные кривые, например окружность, явно представить нельзя. Неявное представление

позволяет обойти это ограничение. Общий вид неявного уравнения второй степени

порождает различные двумерные кривые, называемые коническими сечениями. На рис. 4.20 изображены три вида конических сечений – парабола, гипербола и эллипс. Окружность – это частный случай эллипса. Определяя коэффициенты а, b, c, d, e и f , можно получить разные конические сечения. Если сечение задано относительно локальной системы координат и проходит через ее начало, то f = 0. Для того чтобы провести кривую через данные точки, используются граничные условия.

Пусть с = 1,0, тогда сегмент кривой между точками определяется
пятью независимыми условиями, из которых вычисляются оставшиеся коэффициенты a, b, d, e и f. Например, можно указать положение крайних точек, наклон кривой в них и промежуточную точку на кривой.

Если b = 0 и c =1,0, то аналитическое представление кривой получается с помощью только четырех дополнительных условий в них. Кривая при a = 1,0, b = 0 и c = 1,0 еще проще:

Тремя условиями для вычисления d, e и f могут быть две концевые точки и наклон кривой в одной из них или же две концевые точки и
третья точка на кривой.

Рис. 4.20

При a = b = c = 0 получается прямая линия. Ее уравнение

или

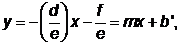
где m – наклон линии; b’ – пересечение с осью у.

Как явное, так и неявное непараметрическое представление осезависимо, т. е. сложность обработки зависит от выбора системы координат. Например, если в заданной системе координат граничным условием является вертикальный наклон, нужно либо изменить ее, либо аппроксимировать бесконечный коэффициент наклона наибольшей допустимой положительной или отрицательной величиной.

Кроме того, если точки на осезависимой непараметрической кривой вычисляются с равномерным приращением по х или у, они не будут равномерно распределены вдоль кривой. Это может повлиять на качество и точность графического изображения. Тем не менее непараметрическое представление бывает полезным. Теперь рассмотрим параметрическое представление, позволяющее обойти эти ограничения.

Параметрические кривые

В параметрическом виде каждая координата точки представлена как функция одного параметра. Значение параметра задает координатный вектор точки на кривой. Для двумерной кривой с параметром t координаты точки

x = x(t),

y = y(t).

Тогда векторное представление точки на кривой:

Чтобы получить непараметрическую форму, нужно исключить t из двух уравнений и вывести одно в терминах х и у.

Параметрическая форма позволяет представить замкнутые и многозначные кривые. Производная, т. е. касательный вектор, есть

где ' обозначает дифференцирование по параметру. Наклон кривой, dy/dx, равен

Отметим, что при x’(t) = 0 наклон бесконечен. Параметрическое представление не вызывает в этом случае вычислительных трудностей, достаточно приравнять к нулю одну компоненту касательного вектора.

Так как точка на параметрической кривой определяется только значением параметра, эта форма не зависит от выбора системы координат. Конечные точки и длина кривой определяются диапазоном изменения параметра. Часто бывает удобно нормализовать параметр на интересующем отрезке кривой . Осенезависимость параметрической кривой позволяет с легкостью проводить с ней аффинные преобразования, рассмотренные в разд. 2 (ч. 1).

На рис. 4.21 сравниваются непараметрическое и параметрическое представления окружности в первом квадранте.

Непараметрический вид

, .

Точки на дуге соответствуют равным приращениям х. При этом дуга состоит из отрезков разной длины, и получается весьма приблизительное графическое представление окружности. Кроме того, расчет квадратного корня – вычислительно дорогостоящая операция.

Стандартная параметрическая форма единичной окружности:

или

, . (4.67)

Рис. 4.21

Параметр θ – геометрический угол, отмеряемый против часовой стрелки от положительной полуоси х. На рис. 4.21, б изображена дуга, построенная по равным приращениям параметра в пределах 0 ≤ θ ≤ p/2. При этом точки располагаются на одинаковом расстоянии вдоль окружности, и окружность выглядит гораздо лучше. Недостаток такого представления – сложность вычисления тригонометрических функций.

Параметрическое представление кривой не единственно, например,

, , (4.68)

также представляет дугу единичной окружности в первом квадранте
(рис. 4.21, в). Связь между параметрическим представлением показана на рис. 4.22. Из него видно, что для единичной окружности

, , ,

, , .

Факт, что уравнение 4.68 представляет дугу единичной окружности, подтверждается следующим:

где r – единичный радиус.

На рис. 4.21, в показан результат для равных приращений t. Он лучше, чем у явного, но хуже, чем у стандартного параметрического представления (4.67). Однако уравнение (4.68) проще с вычислительной точки зрения, т. е. это компромиссное решение.

В случае более сложного параметрического представления бывает удобнее искать значение явной переменной итеративными методами.

Параметрические представления конических сечений осенезависимы и дают более качественное изображение, чем непараметрические; однако оба имеют свои достоинства и недостатки и часто применяются в машинной графике.

Дата добавления: 2018-04-04; просмотров: 1292; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 8 9 10 11 12 13 141516 17 Следующая ⇒

Мы поможем в написании ваших работ!