Комбинированные преобразования

⇐ ПредыдущаяСтр 7 из 17Следующая ⇒

Возможности матричного метода достаточно ясно описаны в предыдущих подразделах. С помощью матричных операций над координатными векторами, определяющими вершины фигур, можно управлять формой и положением поверхности. Однако для получения желаемой ориентации может потребоваться более одного преобразования. Так как операция умножения матриц не коммутативна, то важен порядок выполнения преобразования.

Для иллюстрации эффекта некоммутативности операции умножения матриц рассмотрим преобразования поворота и отражения координатного вектора [х у]. если вслед за поворотом на 90º (посредством [T₁]) производится отражение относительно прямой у = –х (посредством [T₂]), то эти два последовательных преобразования дают

и затем

С другой стороны, если отражение следует за поворотом, то получатся следующие результаты:

и .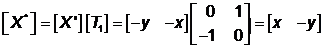

Оба результата различны, что подтверждает важность порядка применения матричных преобразований.

Другое принципиальное обстоятельство иллюстрируется этими результатами и приведенным ниже примером. Ранее отдельные матричные преобразования применялись последовательно к результатам предыдущих преобразований, например

В приведенном ниже примере отдельные преобразования предварительно комбинируются или конкатенируются, а затем полученная матрица применяется к исходному вектору, т. е. [T₁][T₂] → [T₃]и[x y] [T₃]→[x^* y^*].

Пример 4. Комбинированные преобразования на плоскости

Рассмотрим треугольник АВС на рис. 4.10.

Рис. 4.10

Выполним над ним два преобразования: поворот на +90º вокруг точки начала координат

отражение относительно линии у = – х

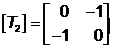Результатом воздействия комбинированного преобразования [T₃] = [T₁][T₂] на треугольник АВС является

или

Получившийся треугольник А^*В^*С^* является конечным результатом данного преобразования, а треугольник А′В′С′ – промежуточным результатом (рис. 4.10).

Проведем преобразование в обратном порядке

или

Конечным результатом будет треугольник D^*E^*F^*, а промежуточным D′E′F′ (рис. 4.10). Оба результата различны, тем самым снова подтверждается важность порядка применения преобразований. Отметим также, что для определителей справедливы равенства det [T₃] = –1 и det[T₄] = –1 и поэтому оба результата могут быть получены с помощью единственного отражения. Треугольник А^*В^*С^* можно получить из АВС путем отражения относительно оси Y (матрица [T₃] и уравнение (4.39)), D^*E^*F^* получается из АВС при отражении относительно оси Х (матрица [T₄]и уравнение (4.39)).

Преобразование единичного квадрата

До сих пор были рассмотрены поведение точек и линий для определения результатов простых матричных преобразований. Однако можно конкретно рассматривать применение матрицы к любой точке плоскости. Как было показано ранее, единственная точка, остающаяся инвариантной при воздействии матричных преобразований, – это точка начала координат. Все другие точки плоскости подвержены преобразованию, которое можно представить как растяжение исходной плоскости, системы координат и перевод в новую форму. Формально принято считать, что преобразование вызывает переход от одного координатного пространства к другому.

Рассмотрим координатную сетку, состоящую из единичных квадратов на координатной плоскости ху (рис. 4.11).

Рис. 4.11

Четыре координатных вектора вершин единичного квадрата, проходящие под одним углом к началу координат, имеют следующий вид:

Такой единичный квадрат изображен на рис. 4.11, а, применяя к нему (2´2)-матрицу общего преобразования, получаем

(4.44)

Результаты этого преобразования показаны на рис. 4.11, б. Из выражения (4.44) следует, что начало координат не подвергается преобразованию, т. е. [A] = [A^*] = [0 0]. Далее отметим, что координаты В^* равны первой строке матрицы преобразования, а координаты D^* – второй. Таким образом, матрица преобразования является определенной, если определены координаты B^* и D^* (преобразование единичных векторов [1 0], [0 1]). Поскольку стороны единичного квадрата первоначально параллельны и ранее было показано, что параллельные линии преобразуются снова в параллельные, то результирующая фигура является параллелограммом.

Влияние элементов a, b, c и d матрицы 2´2 может быть установлено отдельно. Элементы b и c, как видно из рис. 4.11, б, вызывают сдвиг
(см. п. 4.1.1) исходного квадрата в направлениях у и х соответственно. Как отмечалось ранее, элементы а и d играют роль масштабных множителей. Таким образом, (2´2)-матрица задает комбинацию сдвига и масштабирования.

Несложно определить также площадь параллелограмма А^*В^*С^*D^* из рис. 4.11, б, которую можно вычислить следующим образом:

В результате получаем

. (4.45)

Можно показать, что площадь любого параллелограмма А_р, образованного путем преобразования квадрата, есть функция от определителя матрицы преобразования и связана с площадью исходного квадрата А_s простым отношением

(4.46)

Фактически, так как площадь всей фигуры равна сумме площадей единичных квадратов, то площадь любой преобразованной фигуры A_t зависит от площади исходной фигуры A_i

(4.47)

Это полезный способ определения площадей произвольных фигур.

Пример 5. Масштабирование области

Треугольник АВС с координатными векторами [1 0], [0 1] и [-1 0] преобразуется матрицей

образуя новый треугольник А^*В^*С^* (рис. 4.12).

Площадь треугольника АВС равна

Воспользуемся уравнением (4.47), тогда площадь преобразованного треугольника А^*В^*С^* будет равна

Рис. 4.12

Векторы преобразованного треугольника А^*В^*С^* теперь равны

Вычислим площадь, образованную результирующими вершинами:

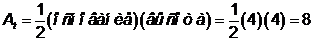Это совпадает с полученным ранее результатом.

Однородные координаты

Выше был рассмотрен ряд преобразований, совершаемых с помощью (2´2)-матрицы общего преобразования. Среди них – поворот, отражение, масштабирование, сдвиг и другие. Ранее отмечалось, что исходная система координат инвариантна по отношению ко всем перечисленным преобразованиям. Однако возникает необходимость изменять положение начала координат, т. е. преобразовывать каждую точку на плоскости. Этого можно достичь путем перемещения точки начала координат или любой другой точки на плоскости

x^*= ax + cy + m,

y^*= bx + dy + n.

К сожалению, нельзя ввести константы перемещения m и n в
(2´2)-матрицу преобразования, так как это не пространство!

Данное затруднение можно преодолеть, используя однородные координаты.

Однородные координаты неоднородного координатного вектора [х у] представляют собой тройку [x′ y′ h], где х = х′/h, y = y′/h, a h – некоторое вещественное число. Заметим, что случай h = 0 является особым. Всегда существует один набор однородных координат вида [х у 1]. Выбрана эта форма, чтобы представить координатный вектор [х у] на физической плоскости ху. Все остальные однородные координаты представляются в виде [hx hy h]. Данные координаты не сохраняют однозначности, например, все следующие координаты [6 4 2], [12 8 4], [3 2 1] представляют физическую точку (3,2).

Матрица преобразования для однородных координат имеет размер 3´3. В частности,

(4.48)

где действие элементов a, b, c и d верхней части (2´2)-матрицы точно соответствует действиям, рассмотренным ранее. Элементы m и n являются коэффициентами перемещения в направлениях х и у соответственно. Полная двумерная матрица преобразования имеет вид

(4.49)

Отметим, что каждая точка плоскости и даже начало координат х = у = 0 теперь могут быть преобразованы.

Дата добавления: 2018-04-04; просмотров: 968; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Мы поможем в написании ваших работ!