Геометрические преобразования на плоскости

Вычислительным аппаратом при построении и применении математических моделей являются матрицы и определители.

Проективная геометрия в аналитическом изложении описывается с помощью матриц.

В качестве элементов матрицы могут фигурировать различные величины: числа, сетки или коэффициенты систем уравнений. Правила в матричной алгебре определяют допустимые операции над элементом. Многие физические задачи удобно выражать в матричном представлении. Для моделей физических систем задача обычно ставится следующим образом: даны матрицы [A] и [B], найти результирующую матрицу [T], такую, что [A] [T]=[B]. В этом случае решением является матрица [Т]=[А]^-1 [В], где [А]^-1– матрица, обратная к квадратной матрице [А].

В то же время матрицу [Т] можно интерпретировать как геометрический оператор. В этом случае для выполнения геометрического преобразования точек, представленных векторами положений в матрице [А], используется умножение матриц. Предположим, что матрицы [А] и [Т] известны. Требуется определить элементы матрицы [В]. Представление [Т] как геометрического оператора является основой математических преобразований, используемых в машинной графике.

Преобразование точек и линий

Изучение математического аппарата, лежащего в основе машинной графики, начинается с рассмотрения способов вывода и преобразования точек и линий. Эти способы наряду с соответствующими алгоритмами рисования используются для изображения объектов или визуализации графической информации. Возможность проводить преобразования точек и линий является фундаментом машинной графики. Нарисованный объект может быть представлен в нужном масштабе, повернут, перемещен или модифицирован в соответствии с требованиями решаемой задачи. Все эти манипуляции с изображением можно выполнить, используя математический аппарат, изложенный в разд. 4.

Изображение и преобразование точек

Точка представляется на плоскости двумя своими координатами, которые определяются как элементы матрицы размером 1´2 [х у].
В трехмерном пространстве используется матрица размером 1´3 [х у z].

Иначе говоря, точка может задаваться в виде вектора – столбца 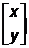в двумерном пространстве или в виде 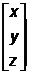– в трехмерном. Строку [х у] или столбец часто называют координатным вектором. Для формирования такого вектора используется матрица – строка, т. е. множество точек, каждая из которых определяет координатный вектор в некоторой системе измерений. Данное множество хранится в компьютере в виде матрицы или массива чисел. Положением точек можно управлять путем манипулирования соответствующей матрицей. Линии, соединяющие точки, формируют отрезки, кривые и картинки.

Рассмотрим результаты умножения матрицы [х у], содержащей координаты точки Р, на матрицу общего преобразования размером 2´2:

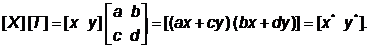(4.1)

Данная запись означает, что исходные координаты точки х и у преобразуются в х^* у^* , где x^*=ax + cy, y^*=bx + by. Представляют интерес значения х^*, у^* – координаты результирующей, преобразованной точки Р.

Рассмотрим некоторые специальные случаи.

При a=d=1 и c=b=0 преобразование сведется к единичной матрице

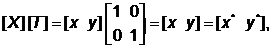(4.2)

и координаты точки Р останутся неизвестными. Как и следовало ожидать, в линейной алгебре умножение на единичную матрицу эквивалентно умножению на 1 в обычной алгебре.

В случае d = 1, b=c=0

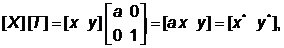(4.3)

где х^* = ах – результат масштабирования координаты Х. Эффект такого преобразования показан на рис 4.1, а. Рассмотрим теперь еще случай b=c=0, т. е.

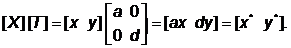(4.4)

Данное преобразование вызывает изменение обеих координат х и у вектора Р (рис. 4.1, б). Если а ≠ d, то координаты масштабируются различным образом. При a = b >1 происходит растяжение вектора Р или масштабирование координат. Если 0 < a = d < 1, то имеет место сжатие.

Если значение а или d отрицательное, то вектор отражается относительно координатных осей или относительно плоскости. Чтобы убедиться в этом, возьмем b = c = 0, d = 1 и a = –1, тогда

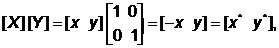(4.5)

и в результате получаем симметричное отражение относительно оси у (рис. 4.1, в). Если b = c = 0, a = 1,d = –1, то выполняется симметричное отражение относительно оси х. Если b = c = 0, a = d < 0, то происходит отражение относительно начала координат, это показано на рис. 4.1, г, где a = –1, d = 1. Заметим, что обе операции отражения и масштабирования зависят только от диагональных членов матрицы преобразования.

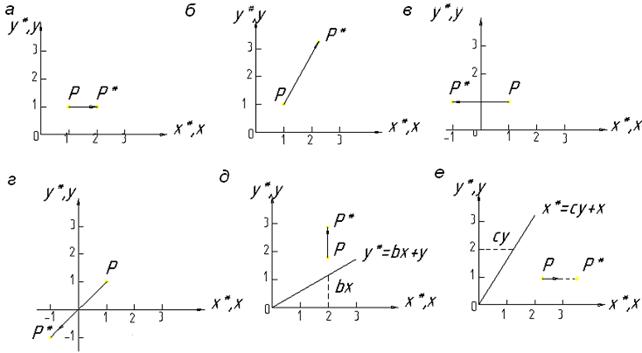
Рис. 4.1

Рассмотрим теперь случай с недиагональными членами. Возьмем сначала значения a=d=1, c=0, тогда

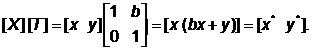(4.6)

Заметим, что координата х точки Р осталась неизменной, тогда как координата у^* линейно зависит от исходных координат. Данное преобразование называется сдвигом (рис. 4.1, д). Аналогично, в случае, когда a = d = 1,
b = 0, преобразование приведет к сдвигу пропорционально координате у (рис. 4.1, е). Таким образом, видно, что недиагональные члены матрицы преобразования создают эффект сдвига координат вектора точки Р.

Прежде чем закончить с преобразованием точек, разберем действие общего преобразования, заданного выражением (рис. 4.1), когда начальный вектор лежит в точке начала координат, т. е.

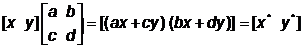Или, в случае начала координат,

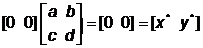Видно, что начало координат инвариантно относительно преобразования общего вида. Это ограничение устраняется при использовании однородных координат.

Преобразование прямых линий

Прямую линию можно определить с помощью двух векторов, задающих координаты ее конечных точек. Расположение и направление линии, соединяющей две эти точки, может изменяться в зависимости от положений векторов. Реальный вид изображения линии зависит от типа используемого дисплея. Рассмотрим только математические операции над конечными точками линии.

На рис 4.2 изображена прямая линия, проходящая между двумя точками А и В. Положение векторов точек А и В задается следующим образом: [А] = [0; 1] и [В] = [2, 3].

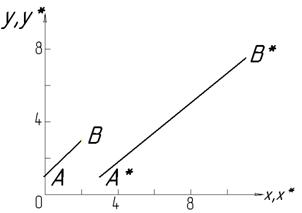Рис. 4.2

Рассмотрим матрицу преобразования

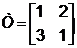, (4.7)

которая, как следует из предыдущего обсуждения, приводит к сдвигу изображения. Преобразование векторов А и В с помощью матрицы [Т] дает новое положение векторов А^* и В^*

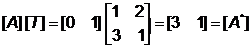(4.8)

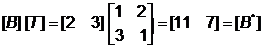. (4.9)

Таким образом, результирующие координаты для точки А^* – это х^*= 3 и у^*= 1. аналогично, В^* – новая точка с координатами х^*=11, у^*=7. в более компактном виде отрезок АВ может быть представлен матрицей размером (2´2):

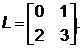
Умножим эту матрицу на [T]:

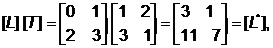(4.10)

где компоненты [L^*] представляют собой преобразование координаты векторов [А^*]и [В^*]. Результат преобразования А в А^* и В в В^* показан на рис. 4.2, где х и у – это исходные оси координат, а х^* и у^* – преобразованные оси. Из рис. 4.2 видно, что преобразование сдвига [Т] увеличивает длину отрезка и изменяет его направление; что (2´2)-матрица преобразует прямую линию у = х + 1, проходящую между точками А и В в другую прямую 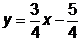, которая проходит между точками А^* и В^*. Фактически с помощью (2´2)-матрицы осуществляется преобразование любой прямой в другую прямую. Все точки преобразованной линии непосредственно соответствуют всем точкам исходной линии. Это достаточно очевидно для конечных точек линии. Рассмотрим теперь преобразование средней точки прямой линии АВ. Допустим, что

[A] = [x₁ y₁], [B] = [x₂ y₂]и .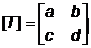

Преобразуем одновременно две крайние точки:

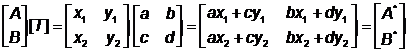. (4.11)

Итак, конечные точки преобразованной линии А^*В^* имеют следующие координаты

(4.12)

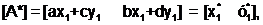
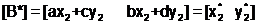Средняя точка отрезка А^*В^* выражается через преобразованные конечные точки

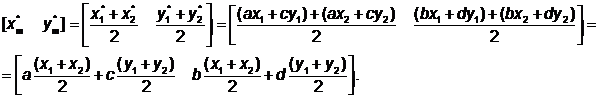(4.13)

Возвращаясь к исходной линии АВ, можно определить среднюю точку следующим образом:

[x_m y_m] = [(x₁+x₂)/2 (y₁+y₂)/2]. (4.14)

Применив матрицу преобразования [Т]к средней точке линии АВ, получаем:

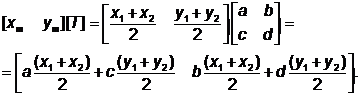(4.15)

Из сравнения выражений (4.13) и (4.15) видно, что они одинаковы, и поэтому средняя точка линии АВ преобразуется в среднюю точку линии А^* В^*. Такой метод можно применить и к любым другим отрезкам разделенной линии. Таким образом, при преобразовании путем умножения на матрицу гарантируется соответствие всех точек линии АВ и А^* В^*.

Дата добавления: 2018-04-04; просмотров: 673; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!