Преобразование: поворот, отражение, масштабирование
Дополнительное изучение рис. 4.3 и примера 2 показывает, что преобразование [Т] включает в себя поворот, отражение, масштабирование. Рассмотрим каждое из этих преобразований отдельно.
Поворот
Рассмотрим плоскость треугольника ABC (рис 4.4) и с помощью следующего преобразования повернем его на 90° против часовой стрелки относительно начала координат
 .
.
|

Если использовать матрицу размером (2´2), состоящую из координат x и у вершин треугольника, то можно записать
 ,
,
что является координатами результирующего треугольника A*B*C*. Поворот на 180° относительно начала координат достигается путем следующего преобразования
 ,
,
а на 270° относительно начала координат – преобразованием
 .
.
Разумеется матрица тождественного преобразования

соответствует повороту вокруг начала координат на 0° или 360°. Обратим внимание, что в этих примерах не встречаются ни масштабирование, ни отражение.
В этих примерах осуществляется преобразование в специальных случаях поворота вокруг начала координат на углы 0°, 90°, 180°, 270°. Как осуществить поворот вокруг точки начала координат на произвольный угол q? Для ответа на этот вопрос рассмотрим вектор положения от начала координат до точки Р (рис 4.5). Обозначим r – длину вектора,
а f – угол между вектором и осью х. вектор положения поворачивается вокруг начала координат на угол q и попадет в точку Р*. Записав векторы положения для Р и Р*, получаем:
|
|
|

и
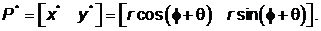
Используя формулу для косинуса суммы углов, перепишем выражение для Р* следующим образом
 .
.
Используя определения для х и у, можно переписать Р* как
 .
.
Таким образом, преобразованная точка имеет координаты


или в матричном виде
 . (4.34)
. (4.34)
|

Итак, преобразование поворота вокруг точки начала координат на произвольный угол θ задается матрицей
 . (4.35)
. (4.35)
Повороты являются положительными, если осуществляются против часовой стрелки относительно точки вращения (рис. 4.5).
Определитель общей матрицы поворота имеет следующий вид:
 . (4.36)
. (4.36)
В общем случае преобразования по матрице с детерминантом, равным 1, приводят к полному повороту.
Предположим теперь, что требуется возвратить точку Р* обратно в Р, т. е. выполнить обратное преобразование. Очевидно, что требуемый угол поворота равен – θ. Из формулы (4.35) возьмем матрицу для выполнения необходимого преобразования
 (4.37)
(4.37)
так как cos(–θ) = cosθ и sin(–θ) = –sinθ. Выражение [T]-1 является формальной записью обратной матрицы [T]. Можно показать, что матрица [T]-1 является обратной к [T], если вспомнить, что результат умножения матрицы на обратную дает единичную матрицу. В данном случае:
|
|
|

где [I] – единичная матрица.
Анализ выражений (4.35) и (4.37) приводит к другому интересному и полезному результату. Вспомним, что транспонирование матрицы определяется заменой её строк столбцами. Обозначим транспонированную матрицу [T] как [T]T. Сравнивая её с [T]-1, видим, что
 . (4.38)
. (4.38)
Обратная матрица вращения является транспонированной. Поскольку формально определитель обратной матрицы вычисляется гораздо сложнее, чем определитель транспонированной, то выражение (4.38) является достаточно важным и полезным результатом. В общем случае обратной для любой матрицы преобразования полного поворота, т. е. матрицы с определителем, равным +1, является её транспонированная матрица (такие матрицы называют ортогональными).
Отражение
В то время, как полный поворот на плоскости ху обычно осуществляется в двумерном пространстве относительно нормали к плоскости, отражение представляет собой тот же поворот на угол 180º в трехмерном пространстве и обратно на плоскость относительно оси, лежащей на плоскости ху. На рис. 4.6 приведены примеры двух отражений на плоскости треугольника DEF. Отражение относительно прямой у = 0 (ось х) получено с использованием матрицы
|
|
|
 (4.39)
(4.39)
В этом случае новые вершины треугольника D*E*F* будут определяться преобразованием

Подобным образом отражение относительно оси у при х = 0 будет иметь вид
 (4.40)
(4.40)
|

Отражение относительно прямой у = х осуществляется с помощью матрицы
 . (4.41)
. (4.41)
Выполнив преобразования, получим координаты вершин треугольника D*E*F*
 .
.
Аналогичным образом отражение относительно оси х будет иметь вид
 . (4.42)
. (4.42)
У каждой из этих матриц определитель равен –1. В общем случае, если определитель равен –1, то преобразование дает полное отражение.
Если оба полных отражения осуществляются последовательно относительно прямых, проходящих через начало координат, то результатом будет полный поворот относительно начала координат. Это можно увидеть, обратившись к следующему примеру.
|
|
|
Дата добавления: 2018-04-04; просмотров: 1908; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
