Пример 2. Пересекающиеся прямые

Рассмотрим две штриховые линии АВ и EF на рис 4.3, конечные точки которых имеют координаты

[А] = [-1 -1], [В] = [3 5/3]

[E] = [-1/2 3/2], [F] = [3 -2].

Уравнение прямой АВ имеет вид –(2/3)х + у = –1/3, а прямая EF задается уравнением х + у = 1.

В матричном виде пучок прямых представляется как

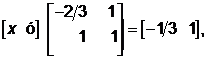
используя матрицу обратного преобразования (4.21), получим точку пересечения этих прямых

Теперь преобразуем эти линии с помощью матрицы

Результирующие прямые А^*В^* и E^*F^* показаны на рис. 4.3. В матричном виде уравнение преобразованных линий имеет вид

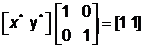
с точкой пересечения .

Преобразуя точку пересечения исходных линий, получим

что тождественно точке пересечения преобразованных линий.

Из рис. 4.3 и примера 2 видно, что исходные штриховые прямые АВ и EF не перпендикулярны друг другу. Однако преобразованные прямые A^*B^* и E^*F^*, показанные сплошной линией, являются перпендикулярными. Таким образом, преобразование [Т] переводит две пересекающиеся неперпендикулярные прямые в две пересекающиеся перпендикулярные. Смысл обратного преобразования [Т]^-1 состоит в переводе двух пересекающихся перпендикулярных прямых в две пересекающиеся, но не перпендикулярные, что может привести к неприятным геометрическим последствиям. Значительный интерес представляет вопрос: при каком условии перпендикулярные прямые преобразуются в перпендикулярные? Рассмотрим сначала более общий вопрос: в каких случаях угол между пересекающимися прямыми сохраняется?

Напомним, что скалярное произведение двух векторов

(4.27)

а векторное произведение двух векторов, принадлежащих плоскости ху, определяется как

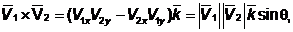(4.28)

где индексы х и у относятся к компонентам х и у вектора, q – острый угол между векторами, а – единичный вектор, перпендикулярный к плоскости ху.

Проведем преобразование , используя (2´2)-матрицу общего преобразования

. (4.29)

Векторным произведением векторов будет

(4.30)

Аналогично, скалярное произведение будет равно

(4.31)

Требуется, чтобы значения векторов, как и угол между ними, оставались постоянными. Сравнивая уравнения (4.27), (4.31) и (4.28), (4.30), а также приравняв коэффициенты подобных членов, получим:

a² + b²=1,

c² + d²=1, (4.32)

ac + bd=0, ,

ad – bc =+1. (4.33)

Выражения (4.32) соответствуют условиям ортогональности матрицы, т. е.

[Т] [Т]^-1= [T] [T]^T= [I]

или

Выражение (4.33) требует, чтобы определитель матрицы преобразования был равен +1.

Таким образом, при полном повороте углы между пересекающимися прямыми сохраняются. Данный результат распространяется также и на операцию отражения, ортогональная матрица которого имеет определитель, равный –1. В этом случае величины векторов сохраняются, но угол между преобразованными векторами в действительности равен (2p – q). Следовательно, в общем случае угол не сохраняется. Однако перпендикулярные прямые преобразуются в перпендикулярные прямые. Поскольку sin(2p – q) = –sinq, ad – bc = –1, полные повороты и отражения называются преобразованиями жесткой конструкции. Кроме того, несколько минут анализа или экспериментирования приводят к выводу, что равномерное масштабирование также сохраняет неизменным угол между пересекающимися прямыми, но не величину преобразуемых векторов. Поскольку ортогональная матрица сохраняет угол между векторами и их величины, матрица однородного масштабирования не является ортогональной.

Дата добавления: 2018-04-04; просмотров: 535; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!