Динамика карданного шарнира неравных угловых скоростей

Если предположить, что при передаче мощности карданным шарниром потерь на трение нет, тогда мощность на ведущем валу  равна мощности на ведомом , т.е.  =  и , где и  – моменты на ведущем и ведомом валах.

Тогда . Наибольшее значение крутящего момента на ведомом валу –  при  = , , ...; наименьшее значение –  при  = , , ...

Отсюда видно, что карданный шарнир передает переменный по величине момент на ведомый вал. Если принять, что массы, связанные с валами карданной передачи, вращаются равномерно, то дополнительный момент, вызванный неравномерностью вращения ведомого вала, будет закручивать карданный вал на угол

,

где  – крутильная жесткость карданного вала.

.                  (5.5)

Возникающее дополнительное закручивание карданного вала может вызвать крутильные колебания в трансмиссии.

 

Расчет элементов карданной передачи

5.3.1 Расчет карданной передачи с шарнирами неравных угловых скоростей

При расчете карданных передач с шарнирами неравных угловых скоростей рассчитываются карданный вал, крестовина, вилки и подшипники карданного шарнира.

Для определения основных размеров карданного вала необходимо определить максимальную частоту вращения карданного вала, соответствующую максимальной скорости автомобиля.

Максимальную частоту вращения карданного вала, соответствующую максимальной скорости автомобиля рассчитывают по формуле:

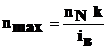,                                                   (5.6)

где  – частота вращения коленчатого вала двигателя при максимальной мощности;  – передаточное число высшей ступени коробки передач;  – коэффициент, зависящий от типа двигателя автомобиля.

Для определения основных размеров карданного вала необходимо также определить расчетный крутящий момент на карданном валу на низшей ступени в коробке передач.

Расчетный крутящий момент на карданном валу определяют по формуле:

.                                               (5.7)

После определения максимальной частоты вращения карданного вала и расчетного крутящего момента на карданном валу выбирают соответствующие стандартные размеры сечений труб карданных валов.

 

 

Критическую частоту вращения карданного вала определяют по формуле:

,                                          (5.8)

где  – внешний диаметр карданного вала;  – внутренний диаметр карданного вала;  – длина карданного вала.

Расчетная критическая частота вращения карданного вала обычно превосходит действительное значение вследствие податливости опор, неточной балансировки вала, наличия зазоров в шлицевых соединениях. Опыт эксплуатации показал, что для удовлетворительной работы карданной передачи необходимо вводить коэффициент запаса по критической частоте вращения:

 = 1,5 ¸ 2,0.                                          (5.9)

Напряжение кручения трубчатого вала рассчитывают по формуле:

,                                                   (5.10)

где  – момент сопротивления сечения кручению.

Допустимые напряжения кручения карданных валов легковых автомобилей - [ ] = 25 ¸ 55 МПа; грузовых автомобилей - [ ] = 100 ¸ 120 МПа.

На жесткость карданный вал рассчитывают по углу закручивания:

,                                                (5.11)

где 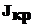 – полярный момент инерции сечения; G – модуль упругости при кручении.

Допустимый угол закручивания – [Q] = 7 ¸ 8° на один метр длины вала.

Размеры крестовины карданного шарнира определяют размеры всего карданного шарнира. Их находят из условий, что крестовина не будет иметь остаточных деформаций под действием меньшей из величин: максимального расчетного крутящего момента на карданном валу, определенного по двигателю или по сцеплению. 

Высоту крестовины карданного шарнира по шипам, исходя из максимального крутящего момента по двигателю, определяют по формуле:

.                        (5.12)

Высоту крестовины карданного шарнира по шипам, исходя из максимального крутящего момента по сцеплению, определяют по формуле:

,                  (5.13)

где  – вес, приходящийся на мост, к которому подводится крутящий момент через рассчитываемую карданную передачу;  – продольный коэффициент сцепления.

По определенной высоте крестовины выбирают соответствующий стандартный типоразмер карданного шарнира.

 

Шипы крестовины карданного шарнира рассчитывают по напряжениям изгиба и среза.

Напряжение изгиба шипа в опасном сечении А-А определяют по формуле:

,                      (5.14)

где  – максимальная нагрузка на шип крестовины;  – длина шипа;  – момент сопротивления сечения шипа изгибу.

При расчете максимальной нагрузки на шип крестовины принимают, что условно сосредоточенная сила действует в середине шипа. Максимальную нагрузку на шип крестовины карданного шарнира рассчитывают по формуле:

,                                               (5.15)

где r – плечо приложения максимальной нагрузки; g – угол наклона валов карданной передачи.

Момент сопротивления сечения шипа изгибу определяют по формуле:

,                                          (5.16)

где  – диаметр шипа крестовины.

Допустимые напряжения изгиба – [ 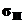] = 250 ¸ 300 МПа.

Напряжение среза шипа крестовины определяют по формуле:

.                                                   (5.17)

Допустимые напряжения среза – [ 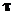] = 60 ¸ 80 МПа.

Вилка карданного шарнира под действием максимальной нагрузки на шип крестовины испытывает изгиб и кручение.

Напряжение изгиба вилки рассчитывают по формуле:

,                                                (5.18)

где с – плечо изгиба.

 Момент сопротивления изгибу для прямоугольного сечения определяют по формуле:

,                                                (5.19)

где b, h – соответственно, высота и ширина сечения вилки карданного шарнира.

Допустимые напряжения изгиба вилки –  [ ] = 60 ¸ 80 МПа.

Напряжение кручения вилки определяют по формуле:

,                                             (5.20)

где а – плечо кручения; – момент сопротивления сечения кручению.

 

 

Момент сопротивления сечения кручению рассчитывают по формуле:

,                                                (5.21)

где  – коэффициент, зависящий от отношения ширины сечения вилки к его высоте.

Допустимые напряжения кручения – [ ] = 120 ¸ 150 МПа.

Игольчатые подшипники карданных шарниров рассчитывают по допустимой нагрузке.

Допустимую нагрузку на подшипник карданного шарнира определяют по формуле:

,                                          (5.22)

где 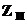 – количество иголок в подшипнике;  – длина иголки;  – диаметр иголки;  - передаточное число до рассчитываемой карданной передачи.

После расчета допустимой нагрузки необходимо проверить полученное значение на соответствие условию:

 > .

 

5.3.2 Расчет карданной передачи с шарнирами равных угловых скоростей

Максимальный момент по сцеплению , Н×м, передаваемый шарниром, определяют по формуле:

,                                                (5.23)

где  – вес, приходящийся на колесо.

Для обеспечения необходимой плавности работы и равномерного распределения нагрузки число шариков в шариковом карданном шарнире с делительным механизмом должно быть четным, поэтому на практике устанавливают четыре (шесть) шариков, равномерно распределенных по окружности.

Допустимое окружное усилие рассчитывают по формуле:

,                                           (5.24)

где Р – окружная сила, действующая на шарик.

Окружную силу, действующую на шарик, определяют по формуле:

,                                                  (5.25)

где R – радиус расположения шариков.

Размеры внутренней обоймы должны обеспечить надежную связь с ведущим валом, и это предопределяет радиус расположения шариков.

Соотношение между радиусом расположения шариков и их диаметрами для обеспечения заданного срока службы рекомендуют определять по эмпирической зависимости:

 = 1,71.

Карданный вал в приводе передних колес – цельнолитой. Поэтому рассчитывают его только по углу закручивания по формуле (5.10), при этом полярный момент инерции для сплошного сечения определяют по формуле:

.                                                   (5.26)

ГЛАВНАЯ ПЕРЕДАЧА

---

Дата добавления: 2018-02-28; просмотров: 1001; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!