Кинематический анализ дифференциала
Для вывода уравнения кинематики дифференциала пользуются обычным приемом остановки водила.
Тогда внутреннее передаточное число будет равно:
, (7.1)
откуда
. (7.2)
Выражение (7.2) называется уравнением кинематики дифференциала.
Если внутреннее передаточное число (кинематический параметр) р = - 1, то дифференциал является симметричным (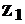 
= 
). Знак «-» указывает на вращение выходных валов в разные стороны при остановленном водиле (корпусе).
Если р ≠ 1 – дифференциал несимметричный.
Значение р для несимметричного дифференциала (применяемого чаще всего в качестве межосевого) выбирается близким значению отношения весовых нагрузок, приходящихся на мосты.
Уравнение кинематики симметричного дифференциала можно получить, подставив в общее уравнение р = -1, тогда:
. (7.3)
Из уравнения (7.3) следуют частные случаи:
1. при движении по прямой ровной дороге – 
(на повороте при уменьшении угловой скорости одного колеса на некоторую величину происходит увеличение угловой скорости колеса на такую же величину);
2. при буксовании одного из колес – 
и 
, либо 
и 
;
3. при торможении центральным трансмиссионным тормозом – 
, тогда либо 
, либо 
.
Динамика дифференциала характеризует распределение моментов между выходными валами. Из условия равновесия внешних моментов, приложенных к дифференциалу, следует:
|
|
|
. (7.4)
Из условия равенства мощностей на корпусе и ведомых валах дифференциала:
, (7.5)
где 
– потери мощности на трение внутри дифференциала.
Используя уравнение кинематики, для симметричного дифференциала можно записать:
. (7.6)
Примем, что 
> 
, т.е. полуось 1 – забегающая, 2 – отстающая, тогда момент на отстающей полуоси будет равен:
; (7.7)
момент на забегающей полуоси:
. (7.8)
Из выражений (7.7), (7.8) видно, что трение в дифференциале изменяет распределение моментов между выходными валами.
В обычном дифференциале момент трения 
весьма мал по сравнению с подводимым моментом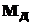 
и почти не влияет на распределение моментов. В этом случае, для симметричного дифференциала моменты на полуосях распределяются поровну:
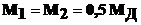. (7.9)
Для несимметричного дифференциала распределение моментов зависит от числа зубьев коронной и солнечной шестерен:
; (7.10)
|
|
|
. (7.11)
Коэффициент блокировки используется для оценки величины внутреннего трения в дифференциале (для оценки величины перераспределения моментов между выходными валами).
Коэффициент блокировки дифференциала можно записать как:
, (7.12)
где 
– момент на отстающей (имеющей меньшую угловую скорость) полуоси, 
– момент на забегающей (имеющей большую угловую скорость) полуоси.
В зависимости от типа и конструкции дифференциала коэффициент блокировки при таком его определении может изменяться от 
= 1 ( = ) до 
= ∞ ( = 0).
Обычно коэффициент блокировки используют в следующем виде:
. (7.13)
При таком определении коэффициент блокировки может изменяться от 
= 0 ( = 0) до = 1 ( 
).
. (7.14)
При использовании формулы (7.13) для симметричного дифференциала можно записать:
; (7.15)
. (7.16)
Для несимметричного дифференциала:
; (7.17)
. (7.18)
|
|
|
Из формул (7.15) – (7.18) видно, что увеличение коэффициента блокировки (увеличение трения в дифференциале) приводит к увеличению силы тяги на колесах автомобиля и улучшает проходимость. Однако при высоких значениях коэффициента блокировки ухудшается управляемость и устойчивость, возрастает нагрузка на одну из полуосей, увеличивается износ шин, расход топлива, снижается КПД.
Коэффициент блокировки шестеренных дифференциалов – = 0,05 ¸ 0,15; кулачковых – = 0,3 ¸ 0,5; червячных – = 0,8.
Симметричный дифференциал, как следует из формулы (7.9), распределяет поровну крутящий момент между ведущими колесами. Это его свойство обеспечивает необходимые устойчивость и управляемость автомобиля при движении на хороших дорогах с твердым покрытием.
Однако указанное свойство симметричного дифференциала ухудшает проходимость автомобиля. При отсутствии потерь на трение ( = 0 и = 0) предельная сила тяги по сцеплению без буксования может быть достигнута только при одинаковых коэффициентах сцепления под ведущими колесами.
Потребный коэффициент блокировки для заданных условий движения можно определить, если подставить в формулу (7.14) максимально возможную разницу коэффициентов сцепления.
|
|
|
Пусть 
= 0,8 (асфальтобетонное покрытие в отличном состоянии) и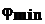 
= 0,1 (сухой лед). Пренебрегая коэффициентом сопротивления качению, имеем:
; 
.
Тогда потребный для движения коэффициент блокировки дифференциала автомобиля с колесной формулой 4 
2, при одинаковой нагрузке на левое и правое ведущие колеса, будет равен:
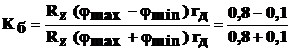≈ 0,8.
Более высокие значения коэффициента блокировки дифференциала не улучшат тяговых свойств автомобиля, кроме случая, когда одно из колес утратит контакт с дорогой (в этом случае желательно иметь = 1).
Т.к. столь значительная разница в коэффициентах сцепления обычно редка, практически считается достаточным для движения в большинстве дорожных условий иметь = 0,3 ¸ 0,8.
Дата добавления: 2018-02-28; просмотров: 715; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!