Повторение ранее изученного материала
УРОКИ ПО МЕТОДИКЕ
23. ОТРИЦАТЕЛЬНЫЕ ЧИСЛА
I. Актуализация знаний
1. Какие числа называются натуральными?
2. Является ли число 0 натуральным?
3. Что такое числовая ось? Что на ней должно быть указано?
4. Изобразите на числовой прямой натуральные числа. 5, 4, 8, 10.
Как расположено на числовой оси предыдущее число по отношению к предыдущему?
II. Постановка учебной задачи
Решить уравнения: 1. х+21=48
2. х-3=6
3. 2х+6=22
4. х+3=3
5. х+1=0
5. Почему мы с вами не можем решить последнее уравнение? (мы не знаем как вычесть из 0 число 1, то есть как вычесть из меньшего числа большее)
6. Мы не нашли такое натуральное число, которое является решением уравнения. Может быть есть еще какие-то числа, среди которых есть корень этого уравнения
7. На последующих уроках нам с вами предстоит научится это делать. А сегодня мы получим новое множество чисел, которое даст возможность решить последнее уравнение.
8. Сформулируйте цель урока (получить новое множество чисел, которое позволит решать уравнения вида х+1=0)
III. Совместное исследование проблемы
При решении этого уравнения введем новое число -1. Это число будем считать решение уравнения х+1=0, то есть -1+1=0
Составим таблицу, в которую будем вносить ваши ответы на вопросы.
Уравнение
х +1=0
х + 2=0
х +3=0
х + n=0
Решение
х =0 - 1
х = -1
Ответ
х = -1
Изображение на числовой прямой
IV. Моделирование
Разобьемся на пары и в парах аналогичным образом решите уравнения х+2=0, х+3=0 (работа в парах, один человек от группы выходит к доске и заполняет таблицу)
|
|
|
Этот процесс можно продолжать и для следующих натуральных чисел.
Обобщим все, что сказали для любого натурального числа n. (заполнить последний столбик)
V. Конструирование нового способа действия.
Выпишите отдельно числа, которые получили при решении уравнений
-1, -2, -3, …,-n, …
Таким образом, мы получили новое множество чисел, которое в математике называется множеством отрицательных целых чисел.
Как назвать множество натуральных чисел? (они называются целыми положительными числами)
Верно. А вот число 0 не является ни положительным, ни отрицательным числом.
А все вместе целые положительные и целые отрицательные числа и число 0 образуют множество целых чисел.
VI. Переход к этапу решения частных задач
Натуральные числа мы изображали на числовой прямой. Как же изобразить на числовой прямой целые отрицательные числа? Где они будут располагаться на числовой прямой?
Рассмотрим частные случаи.
Работа в группах:
Вопросы к группе 1:
1. Изобразите на числовой прямой решение уравнения х+2=5. Покажите стрелкой в каком направлении от числа 5 надо двигаться, чтобы получить решение данного уравнения.
|
|
|
2. Изобразите на числовой прямой решение уравнения х+1=0. Как вы полагаете, в каком направлении от 0 надо двигаться, чтобы получить решение этого уравнения?
3. Определите, какое число предшествует числу -1, -4, -6?
Вопросы к группе 2:
1. Изобразите на числовой прямой решение уравнения х+3=7. Покажите стрелкой в каком направлении от числа 7 надо двигаться, чтобы получить решение данного уравнения.
2. Изобразите на числовой прямой решение уравнения х+2=0. Как вы полагаете, в каком направлении от 0 надо двигаться, чтобы получить решение этого уравнения?
3. Определите, какое число предшествует числу -5, -7?
Вопросы к группе 3:
1. Изобразите на числовой прямой решение уравнения х+4=6. Покажите стрелкой в каком направлении от числа 6 надо двигаться, чтобы получить решение данного уравнения.
2. Изобразите на числовой прямой решение уравнения х+3=0. Как вы полагаете, в каком направлении от 0 надо двигаться, чтобы получить решение этого уравнения?
3. Определите, какое число предшествует числу -2, -8?
Аналогичным образом, покажите решение уравнения х+n=0 на числовой прямой
Определите, какое число предшествует числу – n.
VII. Применение общего способа действия для решения частных задач.
|
|
|
Работа по учебнику
Домашнее задание: выполнить задание…. из учебника теме «Отрицательные числа»
VIII. Рефлексия
27. УМНОЖЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ
Выполнить задания самостоятельно
|
| – каким действием выполнили решение задачи? - а как можно заменить сложение умножением? – Так, где возникло затруднение? – Почему возникло у вас такое затруднение? – Что же нам надо сделать, чтобы выполнить правильно задание и определить, кто его выполнил правильно? – Можем ли сформулировать цели урока. – Хорошо! Чтобы продолжить работу, надо записать тему урока. Кто может сформулировать тему урока? – Запишите тему. (На доске открывается тема урока.) |
| Решим три эти задачи Работа в парах. – Дополните известный алгоритм шагом или шагами, чтобы можно было по нему выполнить умножение дробей \и проверьте на предложенных примерах, как он действует. (У каждой пары на столе таблички из старого алгоритма и несколько чистых листочков. На работу отводится 7 минут). Сравниваем алгоритмы полученные в группах, проводится обсуждение, проверяем его работу на данных дробях -Результатом обсуждения является алгоритм умножения обыкновенных дробей: – Что необходимо знать при умножении обыкновенных дробей? |
| – решите в парах, используя алгоритм, с проговариванием друг другу – выполните проверку ваших решений: кто выполнил без ошибок? У кого один ответ неверный? Почему? Какую ошибку допустили? – Повторим алгоритм записанный на доске. |
|
|
|
29. СЛОЖЕНИЕ ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ
Повторение ранее изученного материала.
Давайте начнем с игры «Да-нет» (слайд 2,3)
1. Два числа, отличающиеся друг от друга только знаками, называются противоположными числами.
2. Для каждого числа есть два противоположных ему числа.
3. Сумма противоположных чисел равна нулю.
4. Модуль числа 0 равен нулю.
5. Модуль числа может быть отрицательным.
6. Противоположные числа имеют разные модули.
7. Из двух отрицательных чисел меньше то, модуль которого больше.
8. Нуль меньше любого отрицательного числа.
9. Нуль меньше положительного числа.
10.Если к любому числу прибавить нуль, то число не изменится.
Следующее задание – сравните числа. (слайд 4)
| 1 вариант | 2 вариант |
| а) -47 и 1 | а) 1 и -100 |
| б) -6,5 и -5,6 | б) -3,9 и -9,3 |
| в) 16 и -360 | в) -25 и -40 |
| г) -18 и -15 | г) -36 и 18 |
Поменяйтесь тетрадями и проверьте. (слайд 5)
| 1 вариант | 2 вариант |
| а) -47 | а) 1 -100 |
| б) -6,5 | б) -3,9 -9,3 |
| в) 16 -360 | в) -25 -40 |
| г) -18 | г) -36 |
Следующее задание - Выполните сложение с помощью координатной прямой. (слайд 6)
Изучение новой темы.
Заполните таблицу. (слайд 7)
| а | b | а+b | |a| | |b| | |a|+|b| |
| -1 | -3 | -4 | 1 | 3 | 4 |
| -2 | -4 | -6 | 2 | 4 | 6 |
| -6 | -1 | -7 | 6 | 1 | 7 |
| -5 | -5 | -10 | 5 | 5 | 10 |
| -9 | 0 | -9 | 9 | 0 | 9 |
-Посмотрите на третий и последний столбцы.
-Что вы можете сказать о числах , расположенных в этих столбцах ?
Поиграем в рассуждалки. (слайд 8)
Сосчитайте (слайд 9)
-Сформулируйте правило сложения отрицательных чисел.
Правило сложения отрицательных чисел. (слайд 10)
Чтобы сложить два отрицательных числа, нужно:1) сложить их модули; 2) перед полученным числом поставить знак минус.
- a + (-b) = - ( │-a │ + │-b │) записать на доске
5. Закрепление темы. Продолжаем работу над темой.
А теперь сосчитайте без помощи координатной прямой. (слайд 12)
- Поиграем в СМОТРИНЫ… (слайд 13)
Даны числа: -1, -2, -3, -4, -5, -6, -7, -8, -9.
Используя каждое число по одному разу, составьте три верных равенства.
-1 + (-4) = -5 -2 + (-6) = -8 -3 + (-7) = -10
Следующее задание – найдите правильный ответ (слайды 14-17)
Последнее задание – заполните пропуски (слайд 18)
Домашнее задание. (слайд 19)
Итог урока (слайд 20)
Мы узнали…
Как сложить два отрицательных числа.
Вспомнили…
Как сравнить положительные и отрицательные числа.
Как сложить два числа на координатной прямой.
31. ИРРАЦИОНАЛЬНЫЕ ЧИСЛА ( 2 СПОСОБА)
1 СПОСОБ
Дата добавления: 2018-02-28; просмотров: 482; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
, 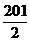 .
. ,2
,2  ,3
,3 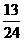 , 4
, 4  .
. м /мин.
м /мин.