Выявление эквивалентных логических выражений и формул
Цели работы:
1) Обобщить теоретические знания по теме: «Эквивалентно-логические выражения и формулы», решить задачи.
2) Рассмотреть алгоритмы решений заданий теме «Эквивалентно-логические выражения и формулы».
3) Формировать умение самоконтроля, рассудительность, терпение, самостоятельность.
Время выполнения: 2 часа.
Теоретические основы
Высказывание - это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции - мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логическое выражение - устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение - логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Логические операции и таблицы истинности
1) Логическое умножение или конъюнкция:
Конъюнкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложное выражение ложно.
Обозначение: F = A & B.
|
|
|
Таблица истинности для конъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
2) Логическое сложение или дизъюнкция:
Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Таблица истинности для инверсии
| A | неА |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То, есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
|
|
|
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность - это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Таблица истинности для эквивалентности
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Порядок выполнения логических операций в сложном логическом выражении
1.Инверсия;
2.Конъюнкция;
3.Дизъюнкция;
4.Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Законы логики отражают наиболее важные закономерности логического мышления. В алгебре высказываний законы логики записываются в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений.
Закон тождества.
Всякое высказывание тождественно самому себе:

Закон непротиворечия.
Высказывание не может быть одновременно истинным и ложным. Если высказывание А истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно:
|
|
|
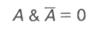
Закон исключенного третьего.
Высказывание может быть либо истинным, либо ложным, третьего не дано. Это означает, что результат логического сложения высказывания и его отрицания всегда принимает значение «истина»:

Закон двойного отрицания.
Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание:

Законы де Моргана.
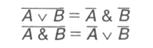
Важное значение для выполнения преобразований логических выражений имеют законы алгебраических преобразований. Многие из них имеют аналоги в обычной алгебре.
Закон коммутативности.
В обычной алгебре слагаемые и множители можно менять местами. В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения:

Закон ассоциативности.Если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или произвольно их расставлять:

Закон дистрибутивности.В отличие от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые:
|
|
|

Рассмотрим в качестве примера применения законов логики преобразование логического выражения. Пусть нам необходимо упростить логическое выражение:

Воспользуемся законом дистрибутивности и вынесем за скобки А:

По закону исключенного третьего  , следовательно:
, следовательно:

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.
Дата добавления: 2018-02-28; просмотров: 1654; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
