Степенная функция с иррациональным показателем
Определение. Степенной функцией с иррациональным показателем называется функция 
, где a - иррациональное число.
Свойства функции , 
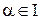
1. Область определения. Посколькустепень с иррациональным показателем a > 0 определена для любого положительного числа и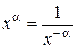 
для a < 0, то 
2. Непрерывность.
Предложение. Функция , 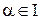непрерывна.
Доказательство. Пользуясь свойствами логарифма, получаем 
. Поэтому функция f непрерывна на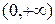 
как композиция непрерывных функций. Докажем, что при a > 0 она непрерывна в точке 0. Пусть r – рациональное число: 
; 
– произвольная последовательность положительных чисел, сходящаяся к 0. Начиная с некоторого номера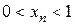 
. Так как показательная функция с таким основанием является строго убывающей и положительна, то 
(*) для этих номеров. Поскольку степенная функция 
с рациональным показателем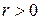 
непрерывна в точке 0, то 
. Переходя в неравенстве (*) к пределу при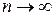 
, получаем 
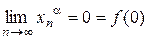. Непрерывность в точке 0 доказана.
3. Четность, нечетность. Функция , , 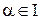не является ни четной, ни нечетной при любом основании а, поскольку ее область определения не является симметричным относительно нуля множеством.
4. Монотонность. Из равенства 
следует, что функция f является композицией 
функций 
и 
. Функция 
является строго возрастающей, функция 
строго возрастает при a > 0 и строго убывает при a < 0. Вывод: если a > 0, функция f строго возрастает; если a < 0, то f строго убывает.
Дата добавления: 2015-12-17; просмотров: 108; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!