Понятие вектора в пространстве. Координаты вектора. Длина вектора. Линейные операции над векторами в координатной форме(сложение, вычитание, умножение на число)
Вектор – направленный отрезок.
,если длина и направление вектора равны
=1
Координаты вектора задают путь из его начала в конец
Опр.: если вектор 
, то 
Понятие вектора в пространстве. Скалярное произведение векторов: определение, вычисление в координатной форме. Угол между векторами, заданными в координатной форме.
Вектор – направленный отрезок.
Опр.: скалярным произведением 2-х векторов называется произведение их длин на cos угла между ними.
12) Кривые второго порядка. Окружность. Эллипс(определение, рисунок, уравнение эллипса эксцентриситет).
Опр.: уравнение 2 порядка:
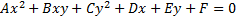
Определяет на плоскости кривую 2 порядка (эллипс, гипербола, парабола)
Окружность – множество точек плоскости, равноудаленных от 1 точки
Уравнение окружности с центром в точке 0 (0;0) .- x2+y2=R2
С центром в точке А(x0;y0)
(x-x0)2+(y-y0)2=R2
Эллипс – множество точек плоскости, сумма расстояний от которых до 2-х данных точек (называемых фокусами) есть постоянная величина равная 2a
2a – большая ось, 2b – меньшая ось
а,b- полуоси, 2с= 
b2=a2-c2
– для точки 0(0;0)
Эксцентриситет Е=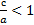 
, чем меньше Е, тем более сплюснут
13) Кривые второго порядка. Гипербола (определение, рисунок, уравнение гиперболы, эксцентриситет)
Опр.: уравнение 2 порядка:
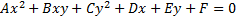
Определяет на плоскости кривую 2 порядка (эллипс, гипербола, парабола)
Гипербола – множество точек плоскости, разность(модуль) расстояний от которых до 2-х данных точек есть постоянная величина равная 2а.
|
|
|
A(x0;y0)
2a – действительная ось, 2b – мнимая ось
Эксцентриситет Е= 
Понятие предела функции. Свойства пределов функции. Первый и второй замечательные пределы.
Опр.: Пределом какой-либо функции F(x) в точке x0 называется число А.
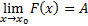
Если x 
x0 ,то f(x) A
Если 
Если 
Свойства:
1.Если f(x) – бб,то 
2. 
3. 
4. 
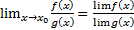
│ замечательный предел:
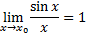
││ замечательный предел:
Непрерывность функции в точке и на отрезке. Свойства непрерывных функций в точке и на отрезке. Точки разрыва первого и второго рода.
Опр.: функция f(x) называется непрерывной если предел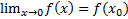 
Функция f(x) непрерывна на 
Свойства:
1.Все элементарные функции непрерывны на своей области определения.
2.Если f(x) и g(x) – непрерывные функции на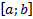 
, то f(x) g(x), f(x) g(x), f(g(x)) - непрерывны на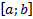
3. 
– непрерывна, но g(x) 
4.Если f(х) – непрерывна на 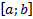и f(a)*f(b)<0, то 
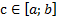и f(c)=0
Точки разрыва:
│рода(не элементарные функции)
a) 
б) 
││ рода(знаменатель равен 0)
Производная функции. Дифференцируемая функция. Основные правила дифференцирования.
Опр.: производной функции f(x) в т. X0 называется предел отношения приращения аргумента, если Δx→0
|
|
|
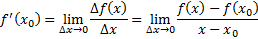
Производная показывает скорость изменения функции.
Механический смысл производной:
S’(t)=V(t), V’(t)=a(t)
Геометрический смысл:
F’(x)=k – коэффициент касательной
Y=kx+b,k=tgα – угол наклона касательной
Опр.: Дифференцируемая функция- функция у которой существует производная
Дифференцирование – нахождение производной
Правила дифференцирования:
1.(с’)=0
2.(c*u)’=c*u’
3.(u±v)’=u’±v’
4.(u*v)’=u’*v+u*v’
5. 
6.f(g(x))’=f’(g(x))*g’(x)
17) Производная функции. Дифференцируемая функция. Формулы дифференцирования степенной функции, показательной функции, тригонометрических функций, обратных тригонометрических функций.
Опр.: производной функции f(x) в т. X0 называется предел отношения приращения аргумента, если Δx→0
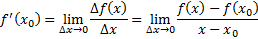
Производная показывает скорость изменения функции.
Механический смысл производной:
S’(t)=V(t), V’(t)=a(t)
Геометрический смысл:
F’(x)=k – коэффициент касательной
Y=kx+b,k=tgα – угол наклона касательной
Опр.: Дифференцируемая функция- функция у которой существует производная
Дифференцирование – нахождение производной.
Формулы дифференцирования:
1.(с)’=0
2.(x)’=1
3.(xn)’=n*xn-1
4.(ax)’=ax*ln a
5.(ex)’=ex
6.(loga x)’= 
|
|
|
7.(ln x)’= 
8.(sin x)’=cos x
9.(cos x )’=sin x
10.(tg x)’ = 
11.(ctg x)’=-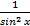 
12.(arcsin x)’= 
13.(arcos x)’=-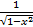 
14.(arctg x)’= 
15.(arcctg x)’=-
18) Дифференциалы первого и второго порядков. Правило Лопиталя-Бернулли.
Опр.: Дифференциалом │ порядка функции f(x) называется dy=y’*dx
││ порядка: d2 y=y’’*(dx)2
Применение дифференциалов в приближенных вычислениях:
Y(x0)≈y(x0)+y’(x0)*Δx
X=x0+Δx
Правило Лопиталя-Бернулли:
Если f(x) и g(x) – бесконечно малые или бесконечно большие функции, тогда 
19) Возрастание и убывание функции. Экстремумы функции. Правило нахождения экстремумов с помощью первой производной.
F(x) возрастает на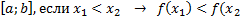 
)
F(x) убывает на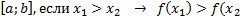 
)
Признак:
F(x) возрастает на 
F(x) убывает на 
Экстремумы – это max и min функции.
X1- точка max,если для (xn) →x1 и f(xn)<f(x1). F(xn)>f(x2)
если х0 – точка экстремума, то f’(x0)=0
Правило:
1.Находим производную f’(x)
2.f’(x)=0
X0- корни
3. 
20) Возрастание и убывание функции. Экстремумы функции. Правило нахождения экстремумов с помощью второй производной. Правило нахождения наибольшего и наименьшего значения функции на отрезке.
F(x) возрастает на )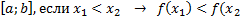
F(x) убывает на )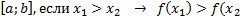
Признак:
F(x) возрастает на
F(x) убывает на
Экстремумы – это max и min функции.
X1- точка max,если для (xn) →x1 и f(xn)<f(x1). F(xn)>f(x2)
|
|
|
если х0 – точка экстремума, то f’(x0)=0
Правило:
1. Находим f’(x),f’’(x)
2. F’(x0)=0
3. F’’(x0)>0, то х0 - точка min, f’’(x0)<0, то х0 – точка max.
Дата добавления: 2022-07-16; просмотров: 116; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!