Определить, в какой форме записана ЗЛП. Ответ обосновать.
1) ) z = – x 1 – 2 x 3 → min
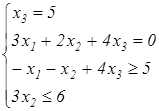
x 1 ≥ 0, x 3 ≤ 0
Сопоставьте полученный ответ с приведенным в скобках.
(Ответ: ЗЛП записана в общей форме, т.к. условия неотрицательности накладываются не на все переменные, система ограничений представлена жесткими и нежесткими условиями, целевая функция стремится либо к max либо к min ) .
2) z = – x 3 – 10 x 4 –5 → max
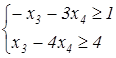
x 3 ≥ 0, x 4 ≥ 0
Сопоставьте полученный ответ с приведенным в скобках
(Ответ: ЗЛП записана в стандартной форме, т.к. условия неотрицательности накладываются на все переменные, система ограничений представлена нежесткими условиями, целевая функция стремится либо к max либо к min ) .
3) z = 3x1 – 3x2 → min
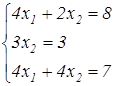
x 1 ≥ 0, x 2 ≥ 0
Решите задачу по образцу, приведенному в №2.2(1,2), письменно, решение вышлите на электронный адрес преподавателя.
2.3 Решить задачи:
Пример № 1.
Преобразовать ЗЛП в каноническую форму
z = х1 – х2 – х3 + 5х4 → max
2х1 – х2 + 3х3 + х4 ≥ 5
х1 + х2 + 6х3 – 7х4 = 2
х1 + 3х2 – 12х3 + х4 ≤ 10
х1 ≥ 0, х2 ≤ 0, х4 ≤ 0
Решение.
1) Вводим новые переменные х′2 = - х2, х′4 = - х4, х′2 ≥ 0, х′4 ≥ 0, х3 = х′3 - х′′3, х′3 ≥ 0, х′′3 ≥ 0 в целевую функцию z =х1 + х′2 + х′′3 - х′3 – 5х′4
2) преобразуем целевую функцию на min:
z ′ = – z = – х1 – х′2 + х′3 - х′′3 + 5х′4 → min
3) Вводим новые переменные в систему ограничений.
|
|
|
2х1 + х′2 + 3(х′3 - х′′3) + х′4 – х5 = 5
х1 – х′2 + 6(х′3 - х′′3) + 7х′4 = 2
х1 – 3х′2 – 12(х′3 – х′′3) – х′4 + х6 = 10
х1 ≥ 0, х′2 ≥ 0, х′3 ≥ 0, х′′3 ≥ 0, х′4 ≥ 0, х5 ≥ 0, х6 ≥ 0
z ′ = – z = – х1 – х′2 + (х′3 - х′′3) + 5х′4 + 0·х5 + 0·х6→ min
Пример № 2.
Преобразовать в каноническую форму
z = –х1 – 3 х3 → max
4х1 + 3х2 + 3х3 = 6
– 4х1 – 2х2 + 3х3 ≤ 8
х1 + 2х3 ≥ 8
х2 ≥ 0, х3 ≤ 0
Решение.
1) Вводим новые переменные
х′3 = - х3, х1 = х′1 – х′′1,
х′3 ≥ 0, х′1 ≥ 0, х′′ 1 ≥ 0, х4 ≥ 0, х5 ≥ 0
в систему ограничений:
4(х′1 – х′′1) + 3х2 – 3х′3 = 6
– 4(х′1 – х′′1) – 2х2 – 3х′3 + х4 = 8
(х′1 – х′′1) – 2х′3 – х5 = 8
в целевую функцию:
z ′ = – z = х1 + 3х3 → min
z ′ = – z = х′1 – х′′1 – 3х′3 + 0·х4 + 0·х5 → min
Пример № 3 .
Решить графическим методом систему линейных неравенств и найти наибольшее и наименьшее значение целевой функции:
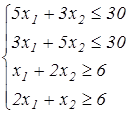
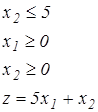
Решение.
Построим прямые по координатам двух точек
| (0;10); | (6; 0) |
| (0; 6); | (10; 0) |
| (0; 3); | (6; 0) |
| (0; 6); | (3; 0) |
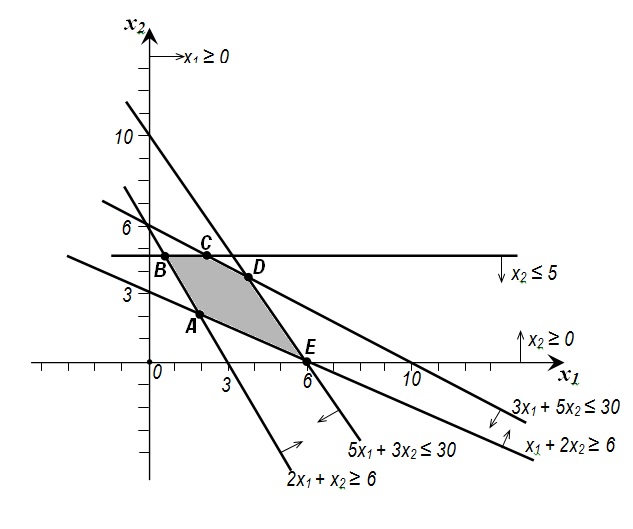
Находим координаты точек А, В, С, D , Е 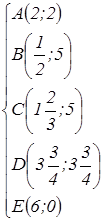
|
|
|
т. А 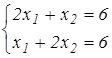
 Δ =
Δ = 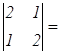 4 – 1 = 3; Δ1 =
4 – 1 = 3; Δ1 =  12 – 6 = 6;
12 – 6 = 6;
Δ2 = 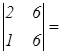 12 – 6 = 6; х1 =
12 – 6 = 6; х1 = 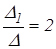 х2 =
х2 = 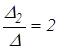
т. В 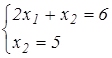
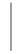 х1 =
х1 =  т. С
т. С 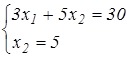
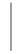 х1 =
х1 = 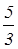 =
= 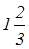
т. D 
 Δ =
Δ = 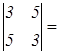 9 – 25 = – 16; Δ1 =
9 – 25 = – 16; Δ1 = 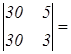 90 – 150 = – 6 0;
90 – 150 = – 6 0;
Δ2 =  90 – 150 = – 6 0; х1 =
90 – 150 = – 6 0; х1 = 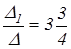 х2 =
х2 = 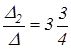
т. Е 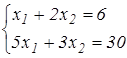
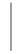 Δ =
Δ =  3 – 1 0 = – 7; Δ1 =
3 – 1 0 = – 7; Δ1 = 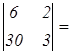 1 8 – 6 0 = – 42;
1 8 – 6 0 = – 42;
Δ2 = 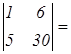 30 – 30 = 0; х1 =
30 – 30 = 0; х1 = 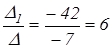 х2 =
х2 = 
Находим значение целевой функции в этих точках и выбираем наибольшее и наименьшее
ZA = Z (2;2) = 5 · 2 + 2 = 12
ZB = Z  = 5 ·
= 5 ·  + 5 =
+ 5 = 
ZC = Z 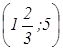 = 5 ·
= 5 · 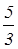 + 5 =
+ 5 = 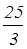 + 5 =
+ 5 = 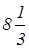 + 5 =
+ 5 = 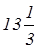
ZD = Z 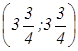 = 5 ·
= 5 · 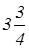 +
+ 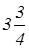 =
= 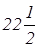
ZE = Z (6;0) = 5 · 6 + 0 = 30
М = ZE (6;0) = 30 т = ZB  =
= 
Ответ: М = ZE (6;0) = 30; т = ZB  =
= 
Задание для самостоятельной работы студентов:
1. Изучив опорный конспект, ответить на вопросы:
Ø Назвать, в каких формах существуют задачи линейного программирования (ЗЛП), в чем особенности каждой из форм;
Ø Алгоритм перехода от одной формы ЗЛП к другой;
Ø Алгоритм графического метода решения задач линейного программирования.
2. Внимательно разобрать образцы решенных примеров, записать их в тетрадь.
3. Построитьна плоскости область допустимых решений системы линейных неравенств и геометрически найти наименьшее и наибольшее значение целевой функции, учитывая х1 ≥ 0, х2 ≥ 0:
|
|
|
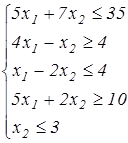
у = –5х1 + х2
4. Преобразовать ЗЛП в каноническую форму:
z = 3х1 + 3х2 → min ;
3х1 – 4х2 ≥ 7,
– х2 ≤ 0,
3х1 – 4х2 = 5,
2х1 – 4х2 ≤ 7,
х2 ≥ 0.
Заключение
Изучение темы «Формы задач линейного программирования» является первым шагом в разделе «Решение задач линейного программирования». Сегодня этот шаг был нами сделан.
Решение задач линейного программирования имеет широкое применение в области экономики и технологии перевозочного процесса, в организации грузовых и пассажирских перевозок, в организации перевозок грузов на особых условиях, что является необходимым условием успешной профессиональной деятельности будущего специалиста, а именно, техника-организатора перевозок. Моделирование экономических, технических и технологических процессов выполняют высокообразованные специалисты, владеющие знаниями из различных отраслей хозяйственной деятельности. Мы с вами выполняем свою задачу, а именно: учимся осуществлять переход в простейших ситуациях от реального технологического процесса к его математической модели, описанной ЗЛП в любой форме, проводить анализ и расшифровку (обратный переход) полученных результатов. Полученные знания повысят конкурентоспособность на рынке труда, позволят будущему специалисту проводить анализ, обобщение и систематизацию исходных данных, а также принимать обоснованные управленческие решения.
|
|
|
Для закрепления полученных знаний и умений необходимо каждому студенту самостоятельно выполнить индивидуальное задание.
И, как никогда, становятся понятными и актуальными слова М. Ломоносова "Математику уже затем учить надо, что она ум в порядок приводит".
Прошу студентов высказать свое мнение о том, чему научились на этом занятии, что нового узнали, что запомнилось лучше, что слабее, какие методы и приемы были более понятными, интересными, каким вопросам в дальнейшем следует уделить больше внимание.
Благодарю всех за сотрудничество!
Итоги занятия
Дата добавления: 2022-06-11; просмотров: 43; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
