Вычислить двумя способами, поменяв порядок интегрирования, в виде двукратного или суммы двукратных интегралов. Изобразить область интегрирования :
;
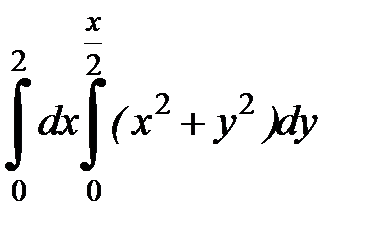Решение.
Область интегрирования D изображена на рис. 2.:
Рис.2. Область интегрирования
Областью интегрирования D является треугольник, ограниченный прямыми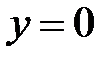 
, 
, 
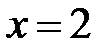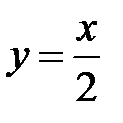(см. рис.2). Здесь 
, 
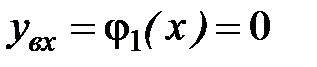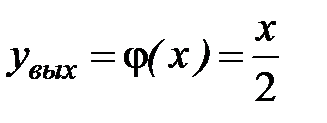(так как точка входа лежит на оси 
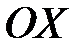, а точка выхода - на прямой 
); 
, 
.
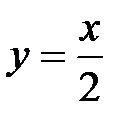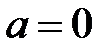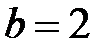Вычислим внутренний интеграл, в котором считаем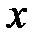 
постоянным: 
.
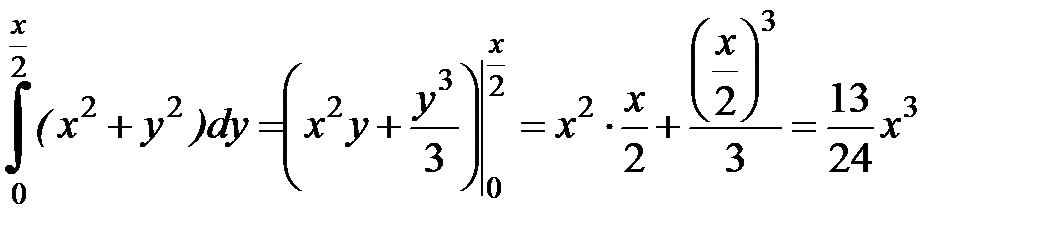Следовательно,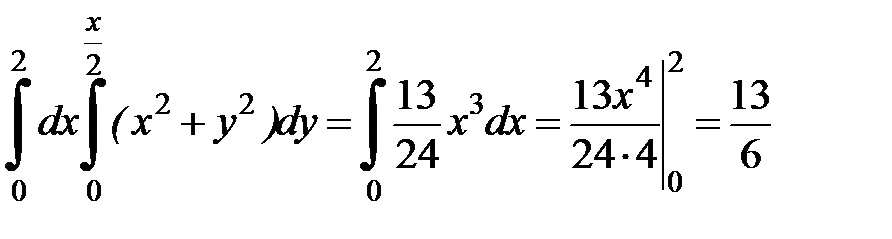 
.
Поменяем порядок интегрирования:
В этом случае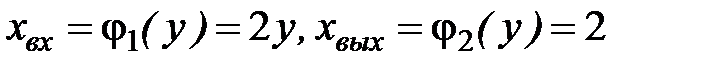 
(так как точка входа лежит на прямой 
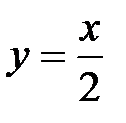или 
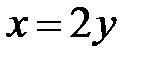, а точка выхода на прямой 
), 
, 
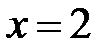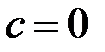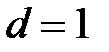, получим 
.
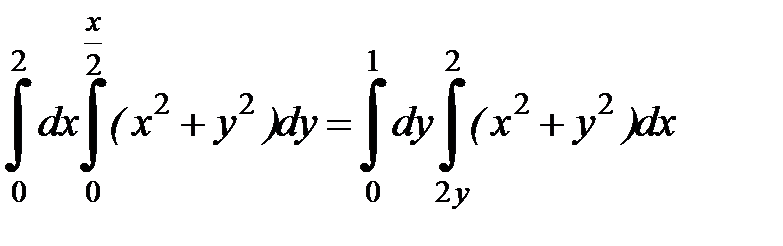Так как
,
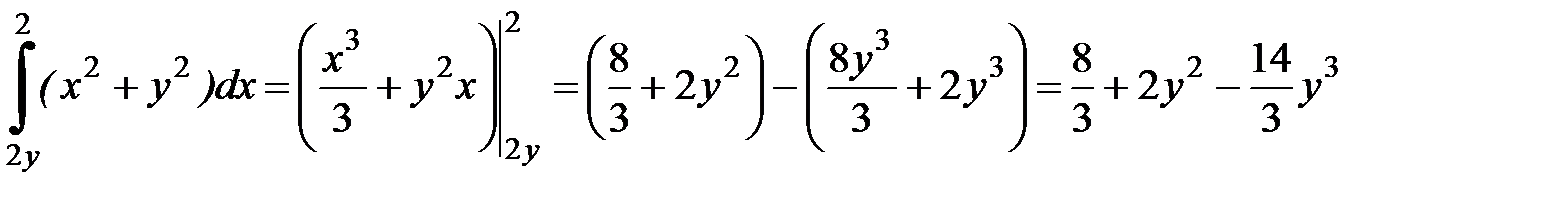то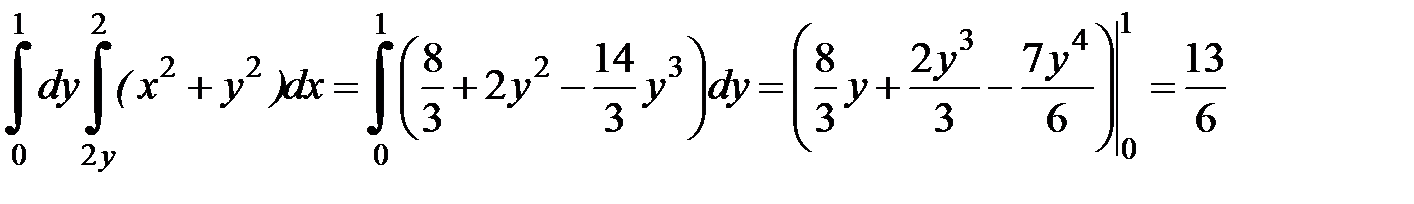 
.
Ответ: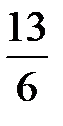 
.
3. Вычислить двойной интеграл по области D, ограниченной указанными линиями, выбрав наиболее удобный путь интегрирования:
a )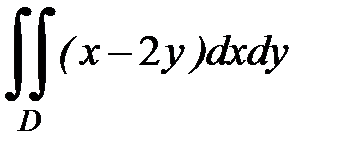 
, D: 
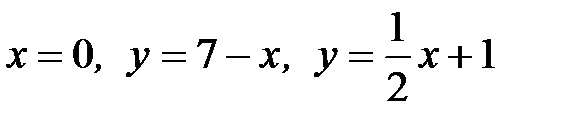
Решение.
Найдем точку пересечения двух графиков:
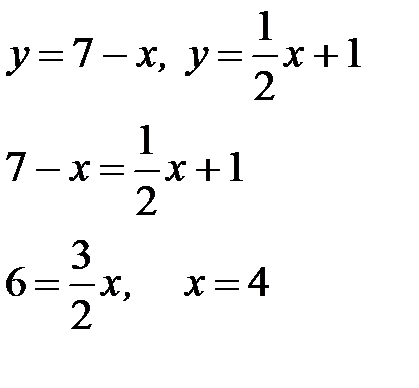
Область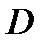 
изображена на рис. 3а
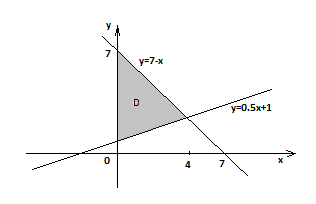
Рис. 3а
Если выбрать внутреннее интегрирование по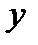 
, а внешнее – по 
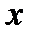, то двойной интеграл по этой области выразится одним повторным интегралом.
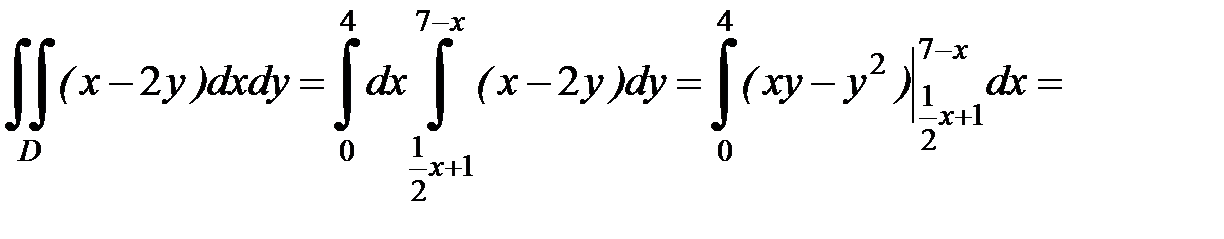
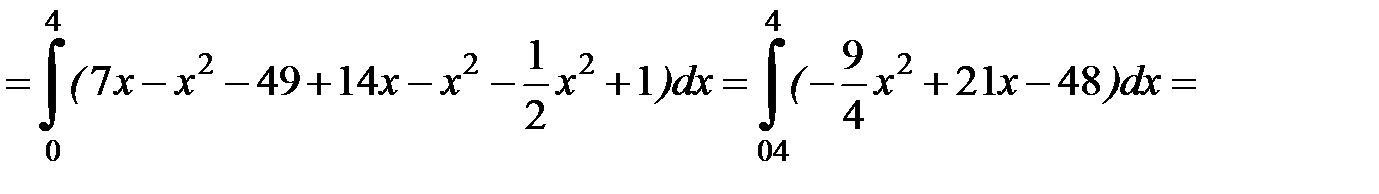
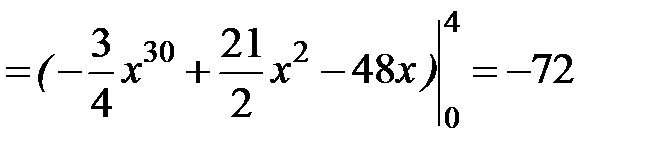
Ответ: -72
б)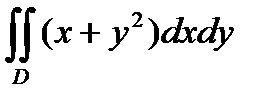 
, D: 
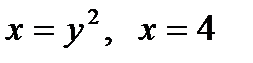
Решение.
Область 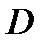изображена на рис. 3б. Выберем внутреннее интегрирование по 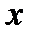, а внешнее – по 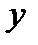, тогда двойной интеграл по этой области выразится следующим образом.
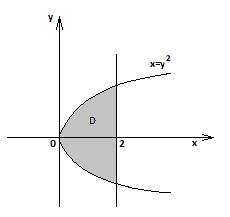
Рис. 3б
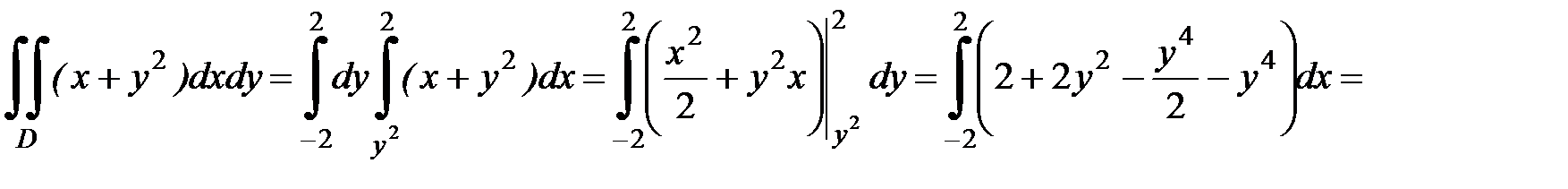
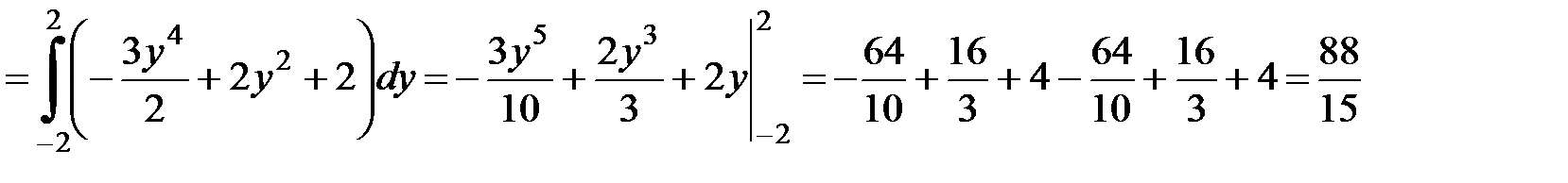
Ответ: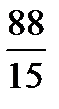 
.
Вычислить двойной интеграл, перейдя к полярным координатам. Изобразить область интегрирования:
;
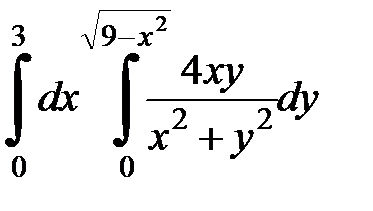Решение.
Область 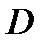изображена штриховкой на рис. 4.
Рис. 4. Область интегрирования
Применяем формулу:
|
|
|
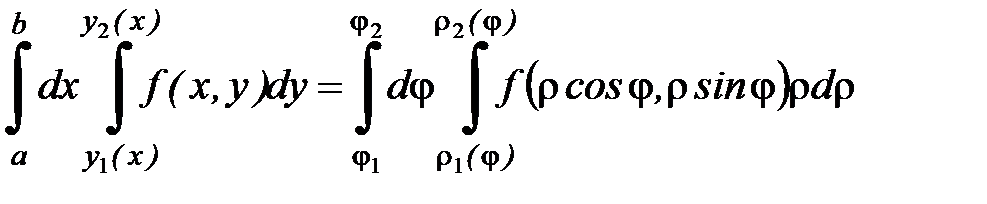
Подставим в подынтегральную функцию полярные координаты:
;
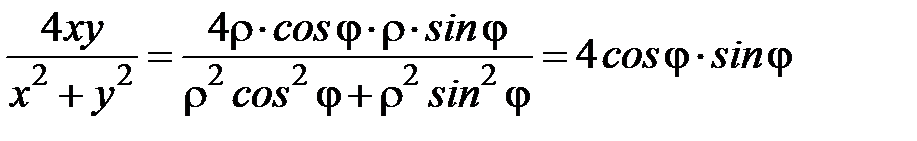Из рис.4 видно, что полярный радиус изменяется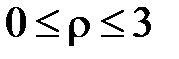 
, а полярный угол изменяется 
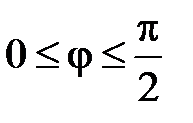. Подставляем в формулу, получаем:
.
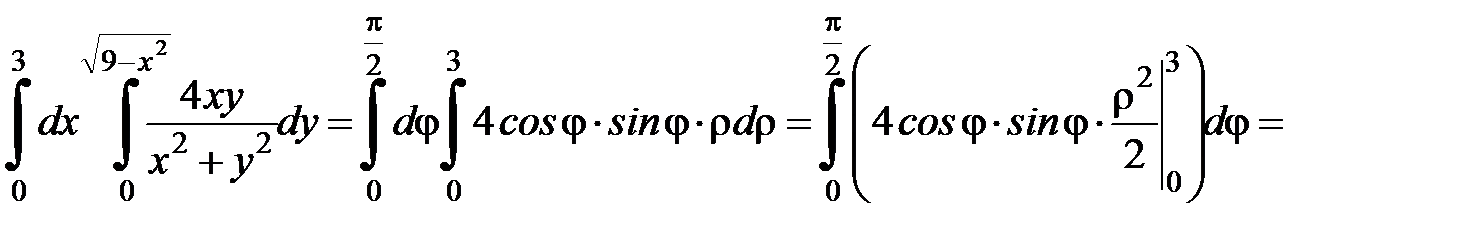
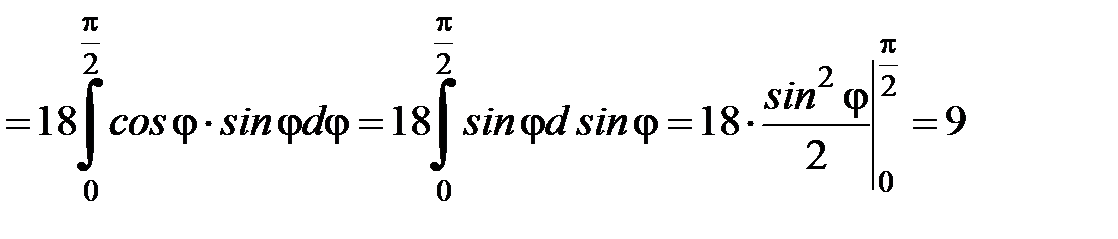Ответ: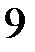 
.
5. Вычислить площадь плоской области D , ограниченной заданными линиями. Изобразить область интегрирования :
: 
, 
, 
.
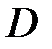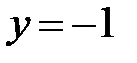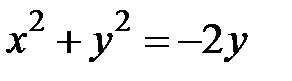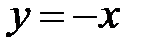Решение:
Область D (рис. 5) данного примера спроектируем на ось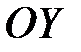 
, которая
проектируется в отрезок [–1; 0] и имеет левой границей линию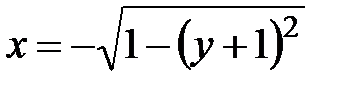 
, а правой – прямую х = –у. Тогда, подставляя в формулу получаем:
.
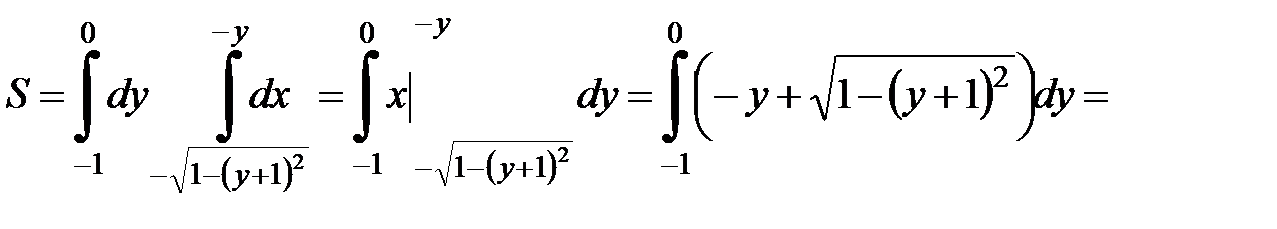
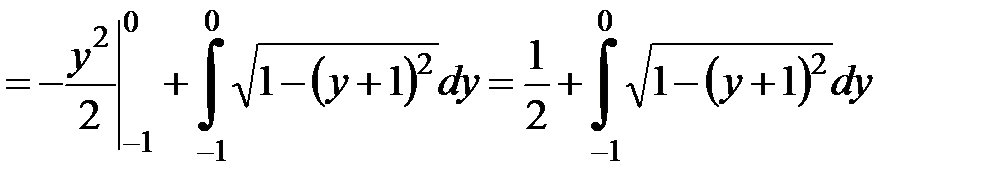| 0 |
| D |
| y |
| x |
| –1 |
Рис. 5 Область интегрирования
.
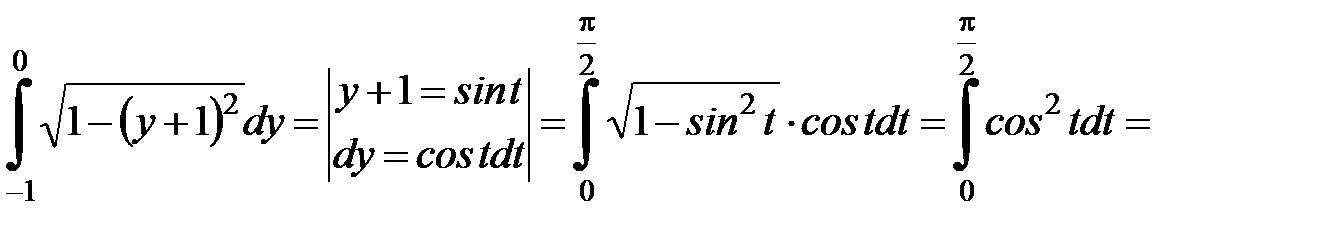
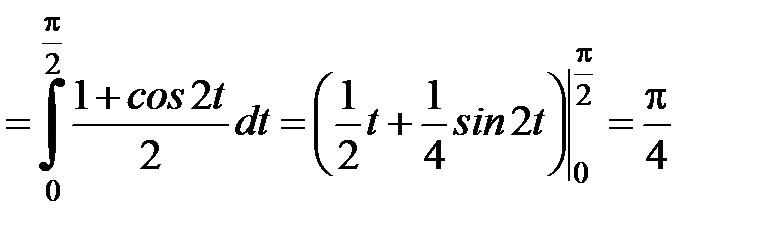Окончательно получаем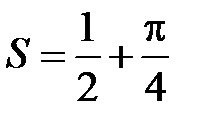 
.
Ответ: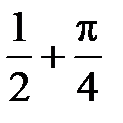 
.
6. Вычислить объем тела, ограниченного указанными поверхностями:
а) V: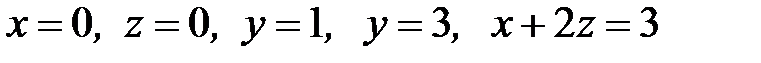 
Решение.
Тело, ограниченное данными поверхностями изображено на рис.6а:
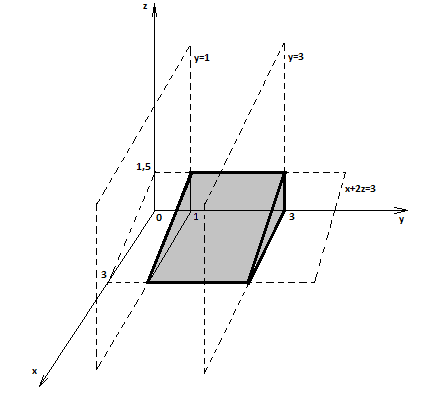
Рис. 6а
Формула для нахождения объема:
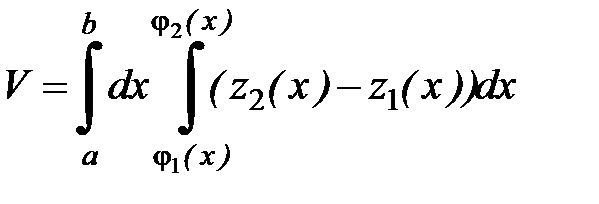
Найдем объем:
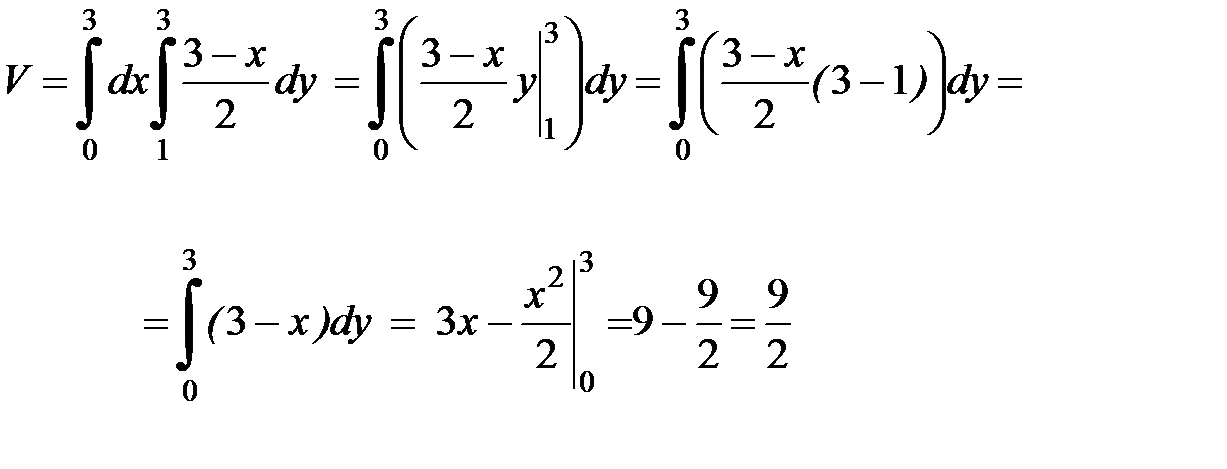
Ответ: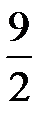 
.
б) V: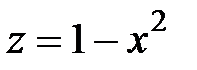 
, 
, 
, 
.
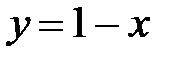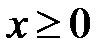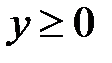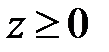Решение.
Тело, ограниченное данными поверхностями изображено на рис.6б:
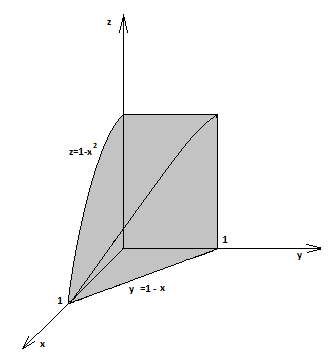
Рис. 6б
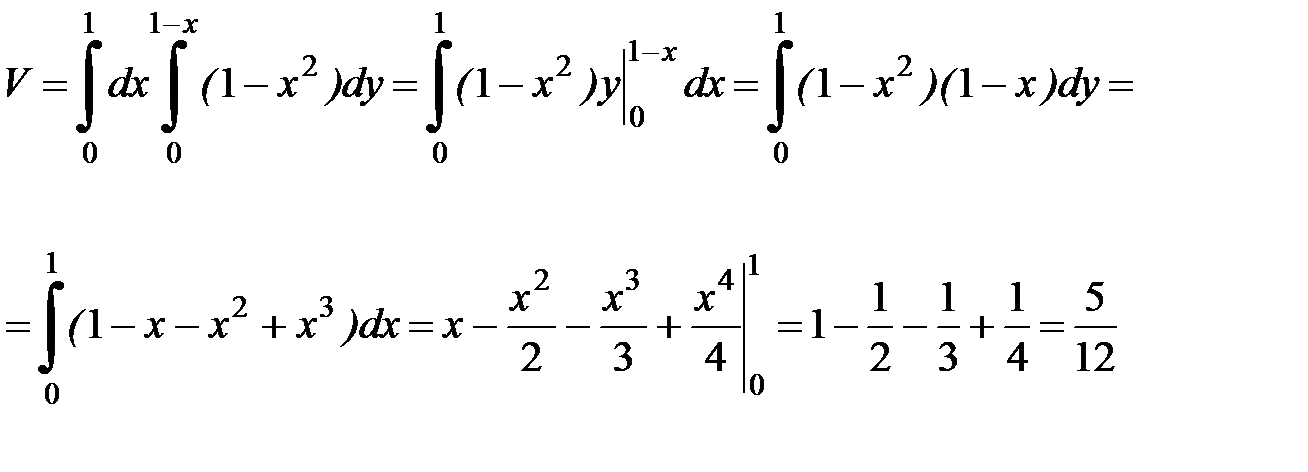
Ответ: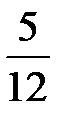 
.
7. Вычислить криволинейный интеграл первого рода:
а)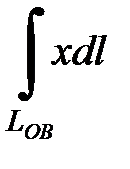 
, где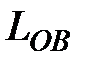 
- отрезок прямой от точки 
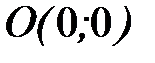до точки 
.
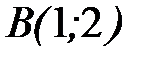Решение.Уравнение прямой: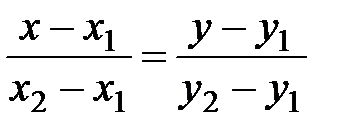 
|
|
|
Подставим координаты точек О и В: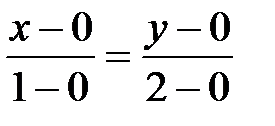 
.
Получаем уравнение прямой: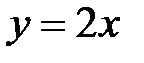 
.
Используем формулу:
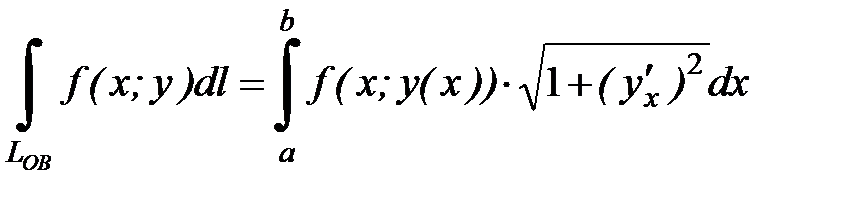
Далее, находим производную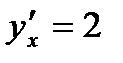 
.
.
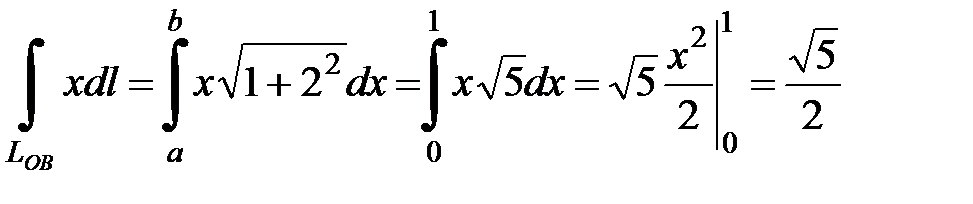Ответ: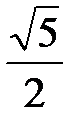 
.
б)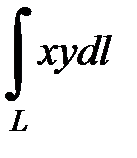 
по дуге окружности 
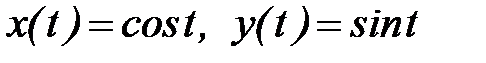при изменении параметра 
.
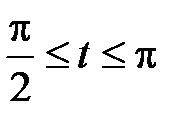Решение. Так как кривая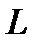 
задана в параметрическом виде, то
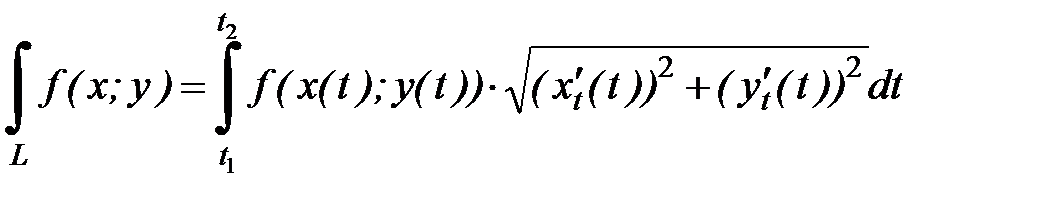
Найдем производные:
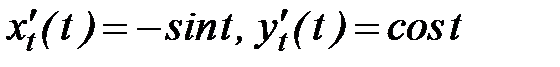
Вычислим исходный интеграл:
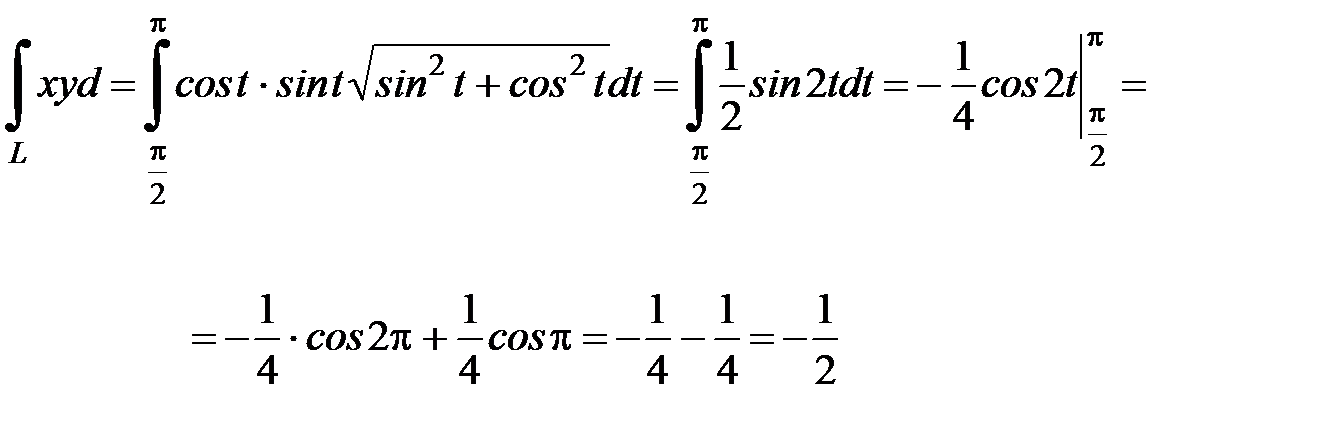
Ответ: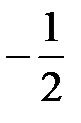 
.
в)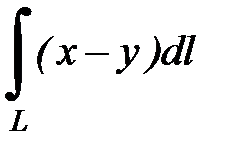 
, где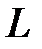 
- вторая четверть окружности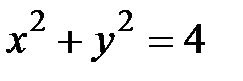 
Решение. Так как кривая 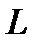представляет собой часть окружность при 
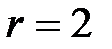то ее удобно задать в полярных координатах: 
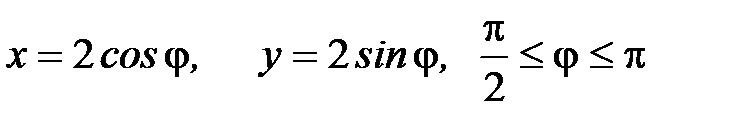. Тогда используем формулу:
Вычислим исходный интеграл:
Ответ: -8.
8. Вычислить данный криволинейный интеграл 2-го рода:
а)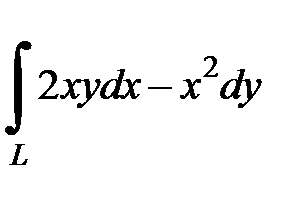 
, где L – дуга параболы 
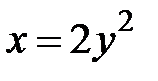, от точки 
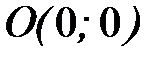до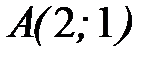 
.
Решение.
Для данного интеграла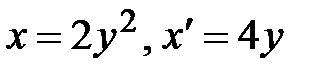 
и при движении из точки 
в точку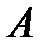 
координата 
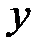меняется от 0 до 1, и по формуле получаем:
.
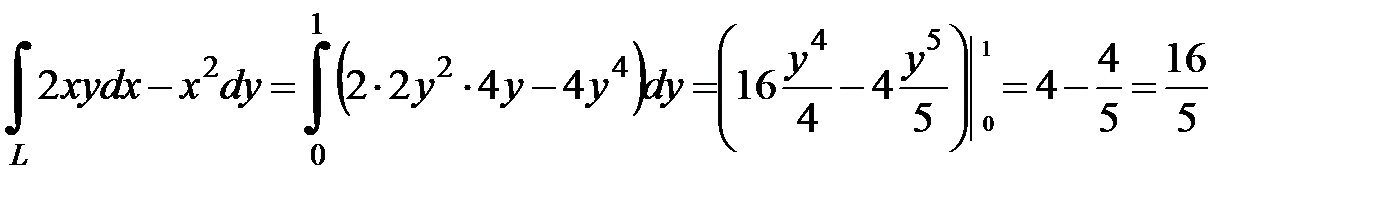Ответ: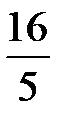 
.
б)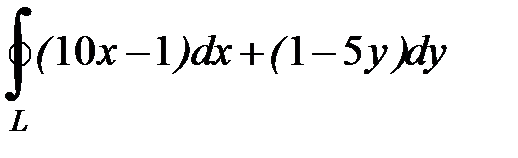 
, где 
- окружность 
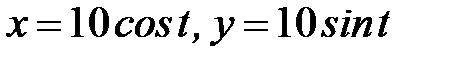при положительном направлении обхода.
Решение.
Так как кривая задана параметрически, то используем формулу
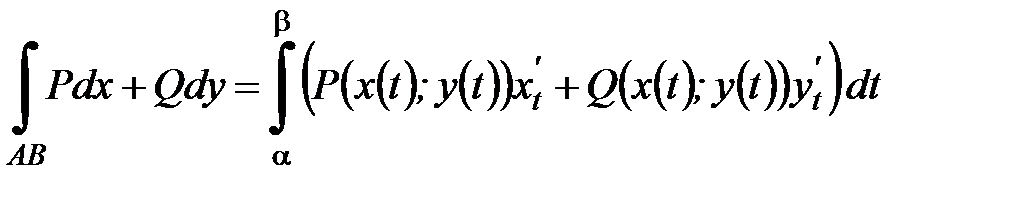
Поскольку интегрирование производится по замкнутому контуру, то параметр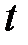 
изменяется 
.
.
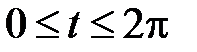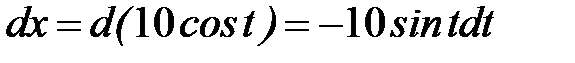
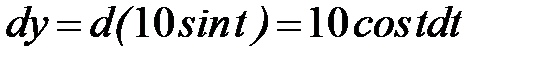
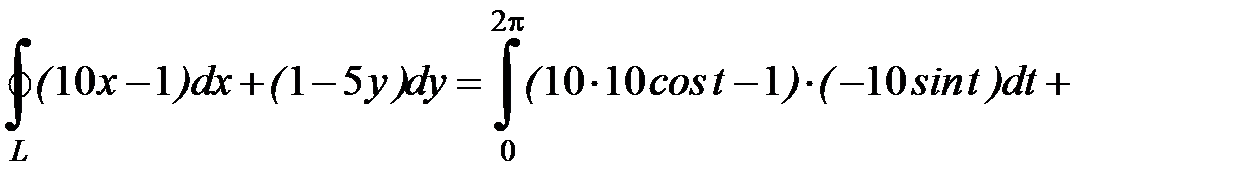
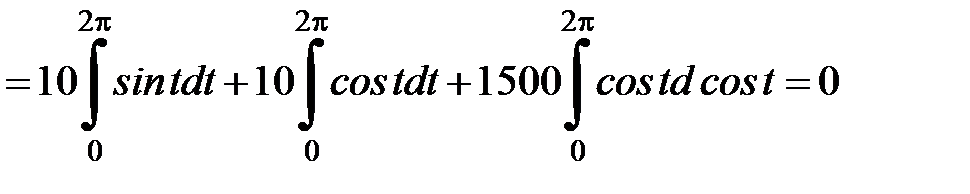Ответ: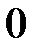 
.
9. Вычислить тройной интеграл:
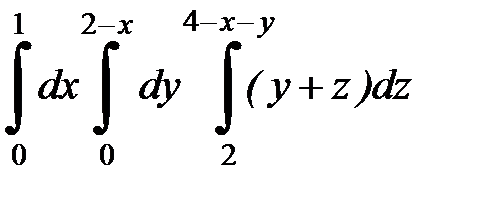
Решение.
Вычисляем внутренний интеграл по переменной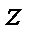 
, считая 
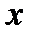и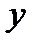 
константами. Получаем:
|
|
|
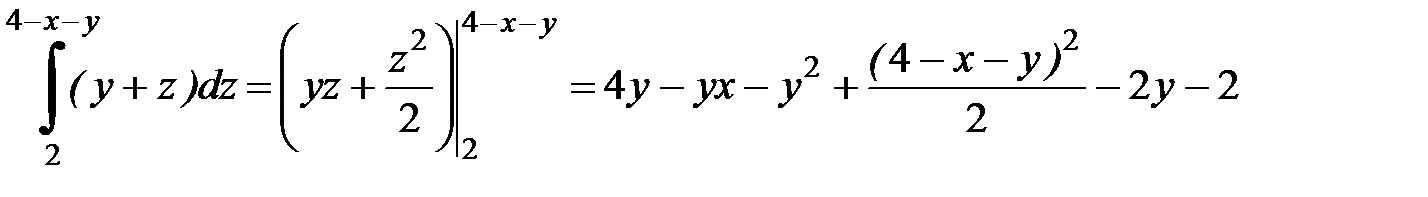
Вычисляем средний интеграл - по переменной y. Получаем:
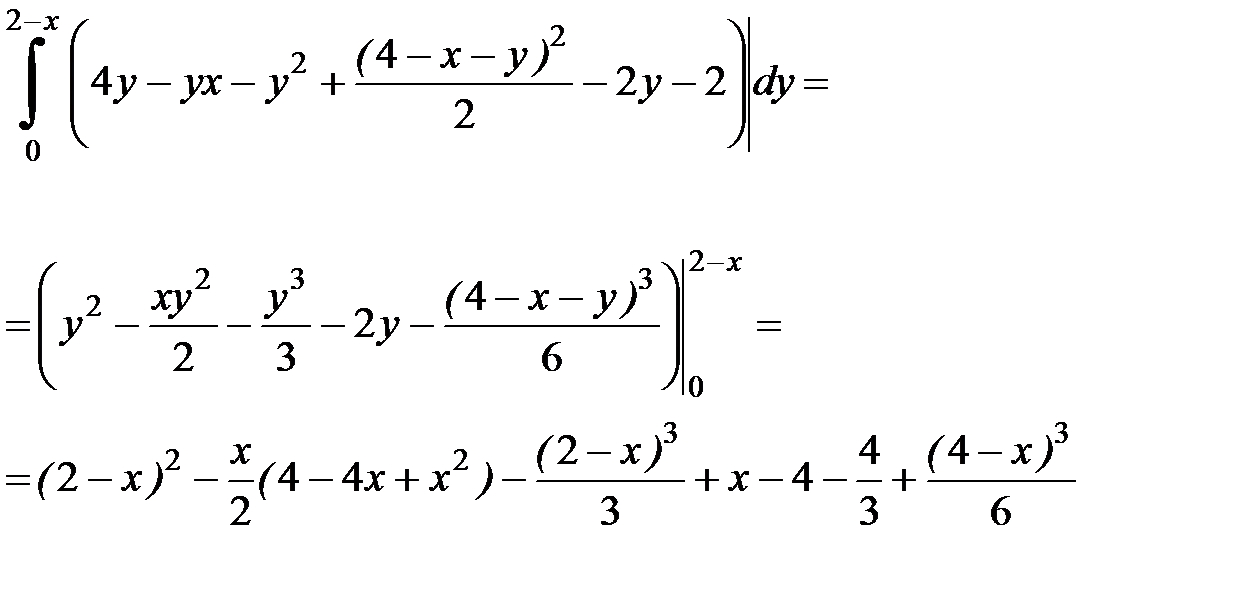
Вычисляем самый внешний интеграл - по переменной x и окончательно находим данный тройной интеграл:
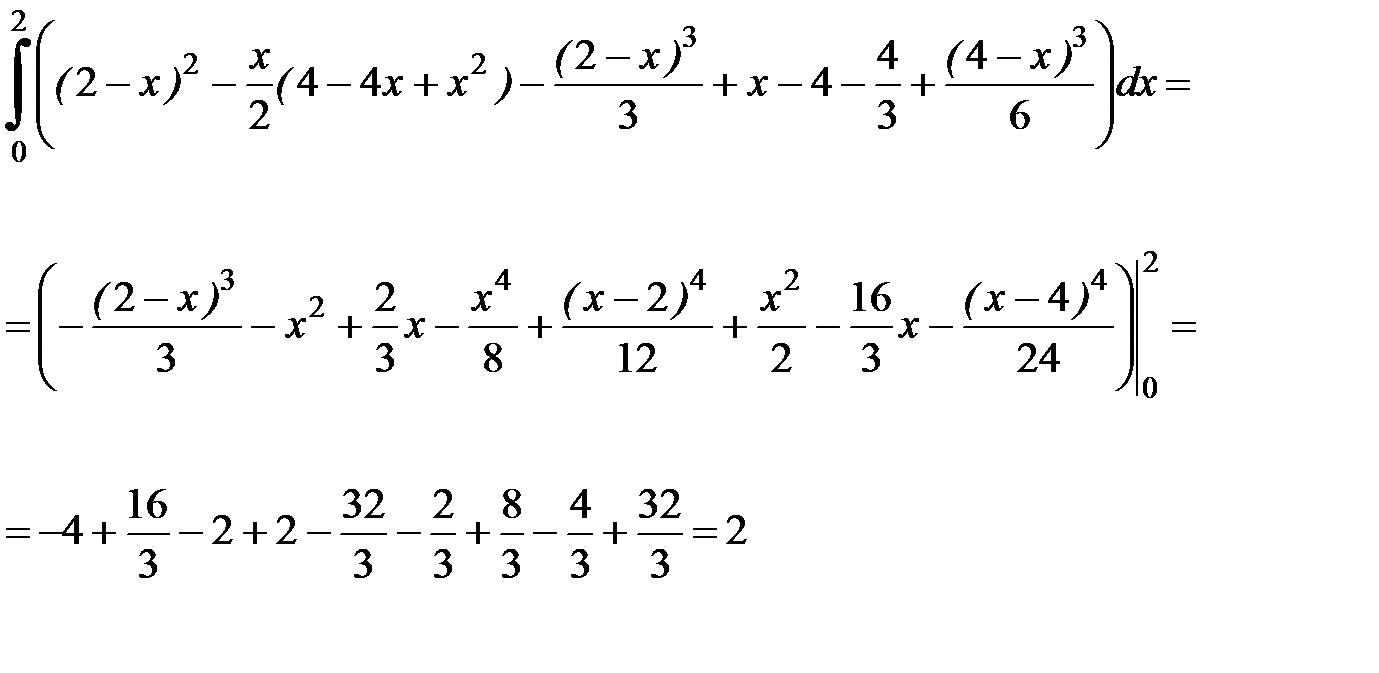
Ответ: 2.
Дата добавления: 2022-06-11; просмотров: 28; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!