Вычислить двойной интеграл, перейдя к полярным координатам. Изобразить область интегрирования:
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
УЛЬЯНОВСКИЙ ИНСТИТУТ ГРАЖДАНСКОЙ АВИАЦИИ
ИМЕНИ ГЛАВНОГО МАРШАЛА АВИАЦИИ Б.П. БУГАЕВА
Кафедра естественно - научных дисциплин
кратные и Криволинейные интегралы
Расчетно-графическая работа
Ульяновск 2018
Кратные и криволинейные интегралы. Расчетно-графическая работа: учебно-методическое пособие / Сост. Бутузова Е.А., Синдяев А.В.
Содержит расчетные задания по разделу математического анализа «Кратные и криволинейные интегралы». Приведены решения типовых задач с подробными объяснениями. Предлагаемые расчетные задания составлены в соответствии с программой раздела курса высшей математики,
Настоящая работа рассмотрена методическим советом УИ ГА, одобрена и рекомендована в качестве учебно-методического пособия для курсантов ульяновского института гражданской авиации при изучении указанного раздела и самостоятельной подготовке.
Содержание
Общие положения.................................................................................................4
Теоретические вопросы...............................................………..….…..............…5
Теоретические упражнения……………………………………………………..6
Расчетные задания.............................………………………..……......................7
Решение типового варианта.....................................………...………................33
|
|
|
Литература............................................................................................................56
ОБЩИЕ ПОЛОЖЕНИЯ
Важным фактором изучения курса высшей математики и практического овладения ее методами является самостоятельная работа курсанта. Типовые расчеты по разделу математического анализа «Кратные и криволинейные интегралы» предназначены для развития и активизации самостоятельной работы курсантов по указанной теме .
Типовой расчет содержит теоретические вопросы, теоретические упражнения и расчетную часть. Теоретические вопросы и теоретические упражнения - для всех курсантов учебной группы, а задачи - для каждого курсантам выдаются по вариантам.
В типовых расчетах принята следующая нумерация: первое число означает номер задания, а второе - номер варианта.
Ответы на теоретические вопросы курсант готовит устно, а теоретические упражнения и расчетные задания - письменно по мере изучения учебного материала на лекциях и практических занятиях. Завершающим этапом является защита типового расчета. Во время защиты курсант должен уметь правильно отвечать на теоретические вопросы, объяснять решения теоретических упражнений и задач, решать задачи аналогичного типа.
|
|
|
1. ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ
1. Определение двойного интеграла. Его геометрический и физический смысл.
2. Основные свойства двойных интегралов.
3. Теорема о среднем для двойного интеграла.
4. Вычисление двойных интегралов двумя последовательными интегрированиями (случай прямоугольной области).
5. Вычисление двойных интегралов двумя последовательными интегрированиями (общий случай).
6. Замена переменных в двойном интеграле.
7. Двойной интеграл в полярных координатах.
8. Привести примеры применения двойного интеграла в технических приложениях.
9. Определение тройного интеграла. Его физический смысл.
10. Основные свойства тройных интегралов.
11. Вычисление тройного интеграла с помощью перехода к двойному.
12. Определение криволинейного интеграла первого и второго рода.
13. Свойства криволинейных интегралов первого и второго рода.
14. Теоремы о вычислении криволинейных интегралов.
15. Сравнительный анализ криволинейных интегралов первого и второго рода.
16. Теорема Грина.
ТЕОРЕТИЧЕСКИЕ УПРАЖНЕНИЯ
1. Доказать равенство 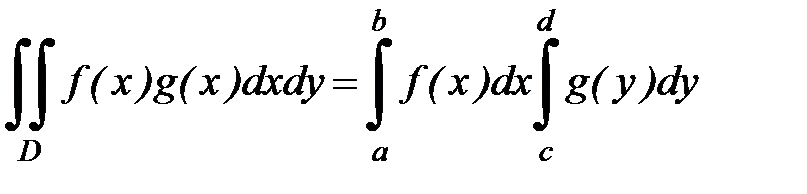 ,
,
если D – прямоугольник 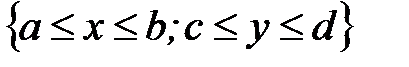 .
.
2. Пользуясь определением двойного интеграла, доказать, что 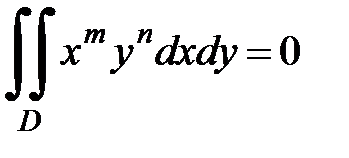 , где D – прямоугольник
, где D – прямоугольник 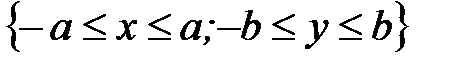 , если m,n – натуральные числа и, по меньшей мере, одно из них нечетно.
, если m,n – натуральные числа и, по меньшей мере, одно из них нечетно.
|
|
|
3. Доказать формулу Дирихле: 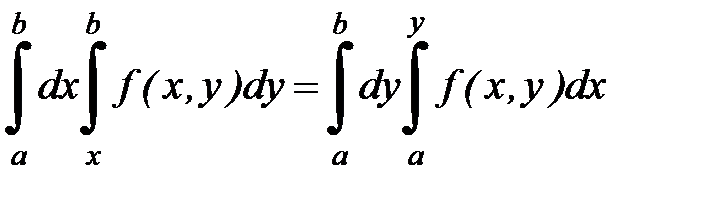 ,
,
4. Пользуясь формулой Дирихле, доказать равенство:
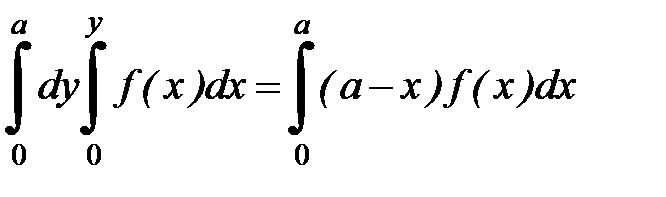
5. Определить, какой интеграл больше 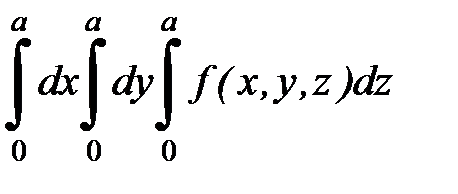 или
или
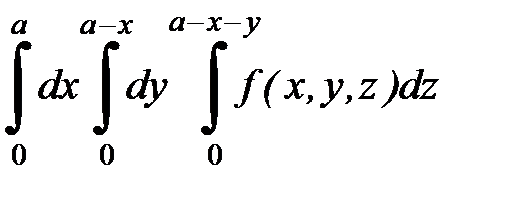 , если
, если 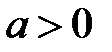 и
и 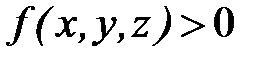 ?
?
6. Доказать теорему о среднем для криволинейного интеграла 1-го рода:
Если функция 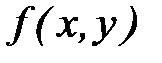 непрерывна на кривой
непрерывна на кривой 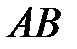 длиной
длиной  , то на этой кривой
, то на этой кривой 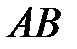 найдётся точка с координатами
найдётся точка с координатами 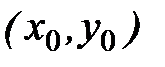 такая, что
такая, что
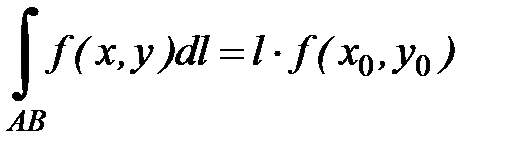
7. Доказать, что криволинейный интеграл 2-го рода 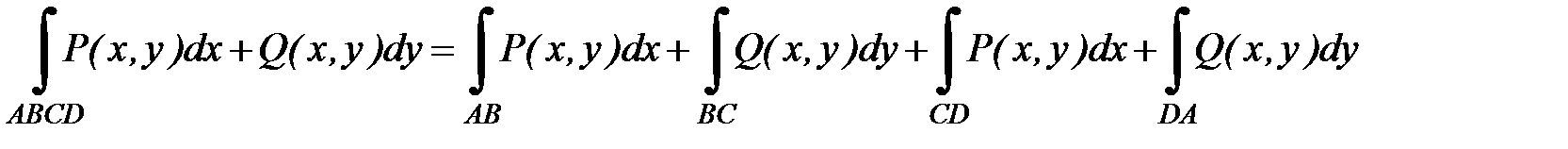 , если
, если 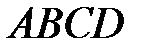 - прямоугольник, в котором стороны
- прямоугольник, в котором стороны 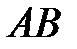 и
и 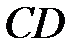 параллельны оси
параллельны оси 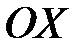 .
.
РАСЧЕТНЫЕ ЗАДАНИЯ
1. Вычислить двойной интеграл по области D , ограниченной указанными линиями:
1.1. 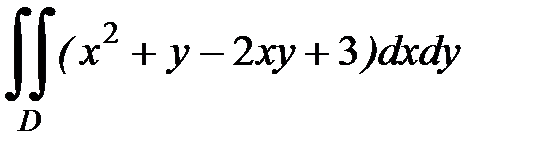 , D:
, D: 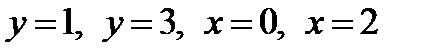 .
.
1.2. 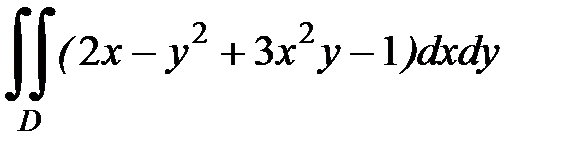 , D:
, D: 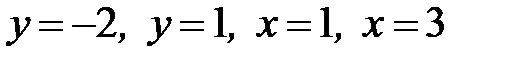 .
.
1.3. 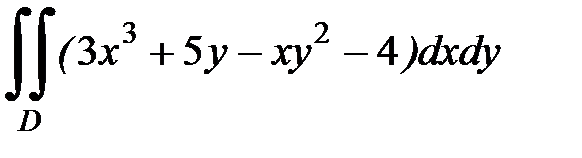 , D:
, D: 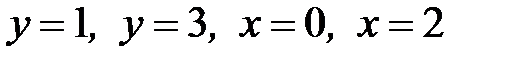 .
.
1.4. 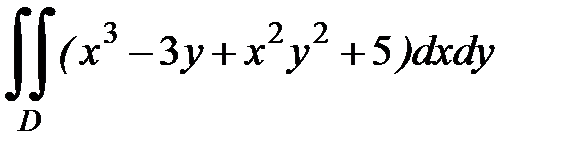 , D:
, D: 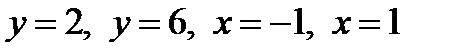 .
.
1.5. 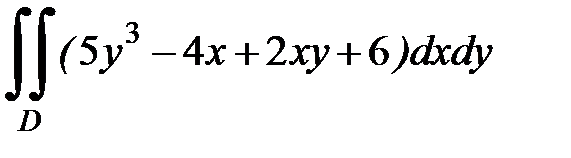 , D:
, D: 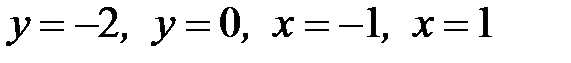 .
.
1.6. 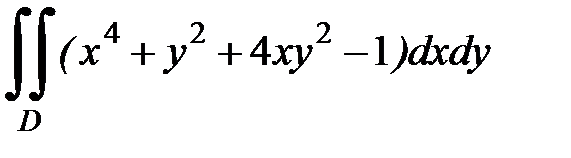 , D:
, D: 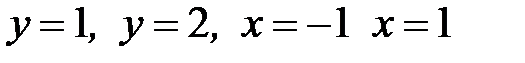 .
.
1.7. 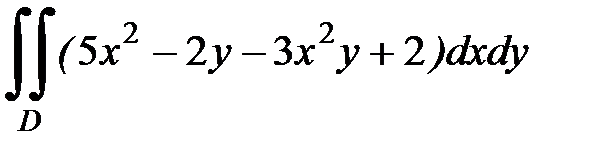 , D:
, D: 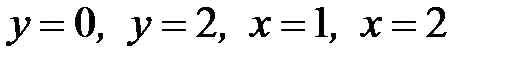 .
.
1.8. 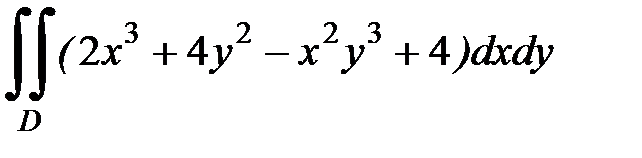 , D:
, D: 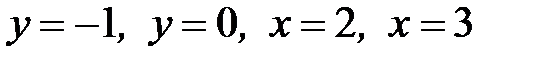 .
.
1.9. 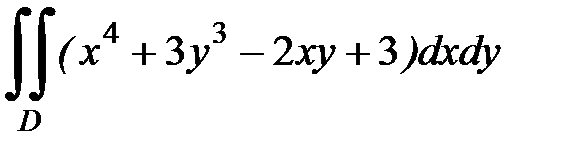 , D:
, D: 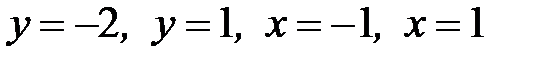 .
.
1.10. 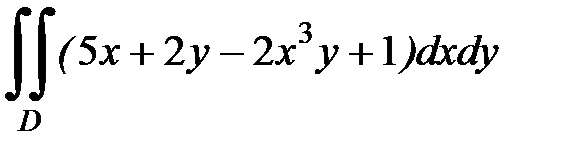 , D:
, D: 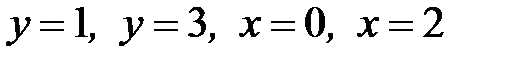 .
.
1.11. 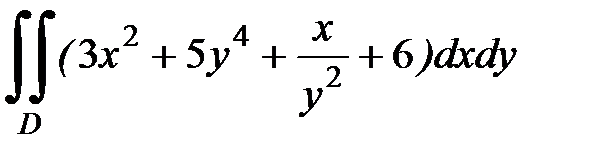 , D:
, D: 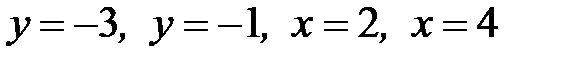 .
.
1.13. 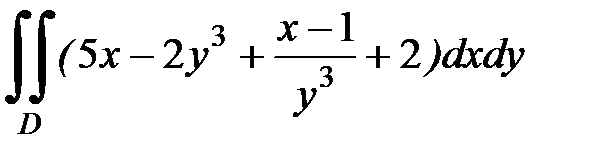 , D:
, D: 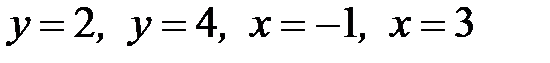 .
.
1.14. 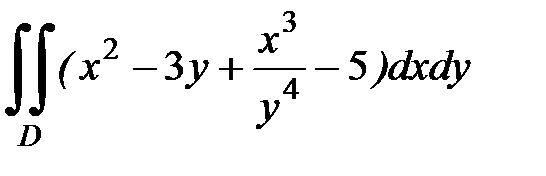 , D:
, D: 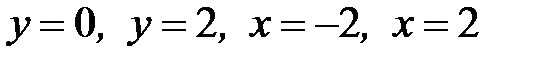 .
.
1.15. 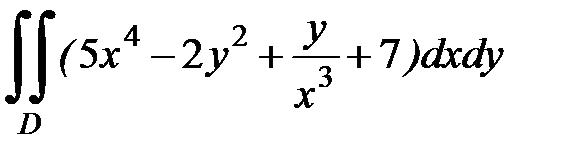 , D:
, D: 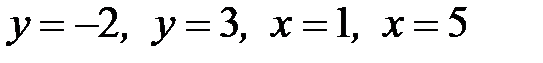 .
.
1.16. 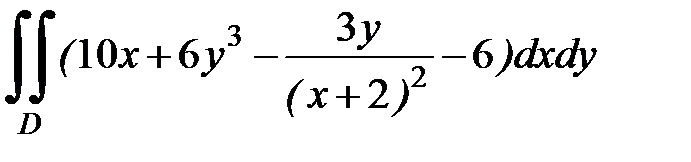 , D:
, D: 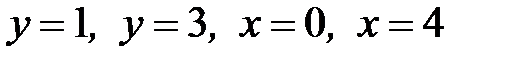 .
.
1.17. 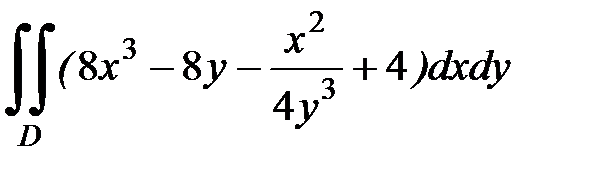 , D:
, D: 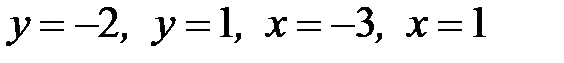 .
.
1.18. 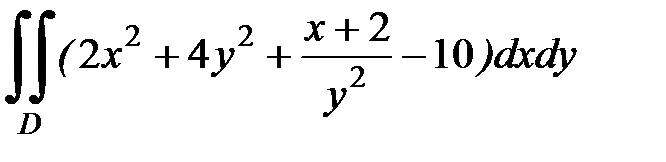 , D:
, D: 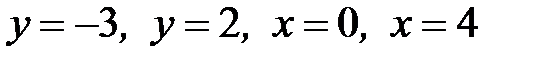 .
.
1.19. 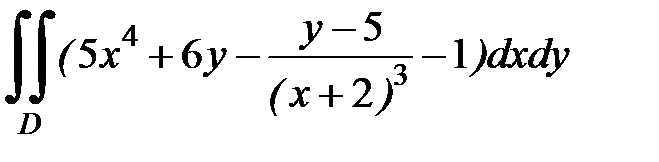 , D:
, D: 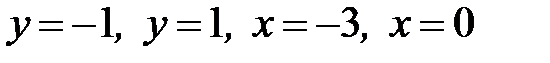 .
.
1.20. 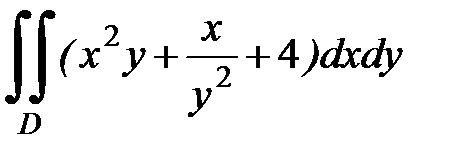 , D:
, D: 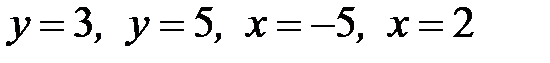 .
.
1.21. 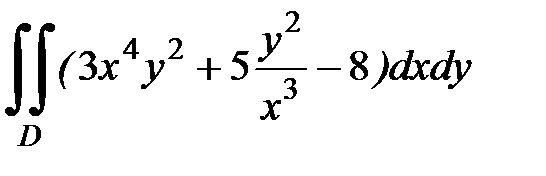 , D:
, D: 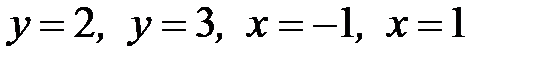 .
.
1.22. 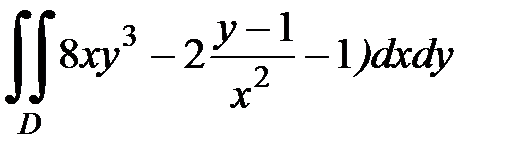 , D:
, D: 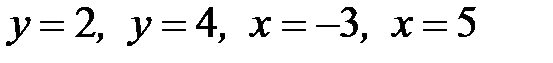 .
.
1.23. 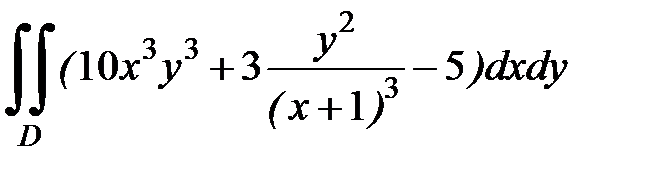 , D:
, D: 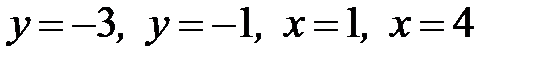 .
.
1.24. 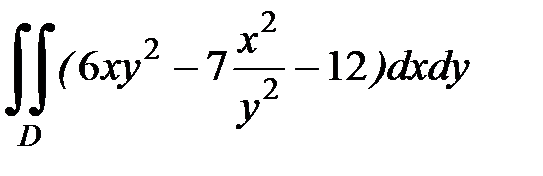 , D:
, D: 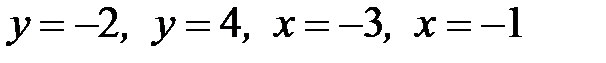 .
.
1.25. 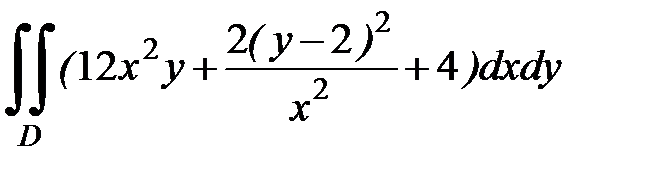 , D:
, D: 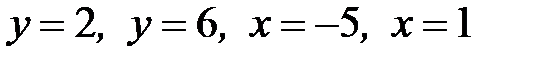 .
.
1.26. 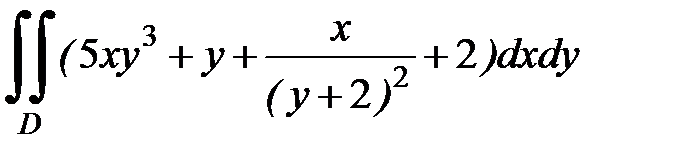 , D:
, D: 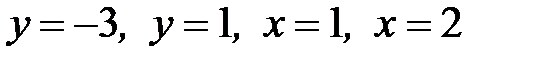 .
.
1.27. 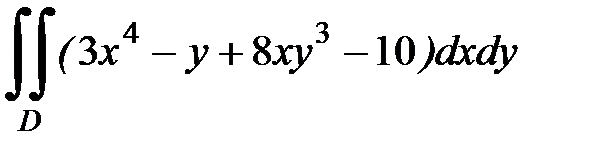 , D:
, D:  .
.
1.28. 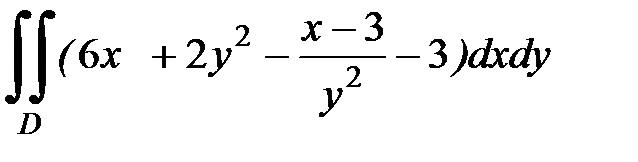 , D:
, D: 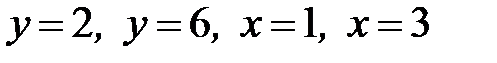 .
.
1.29. 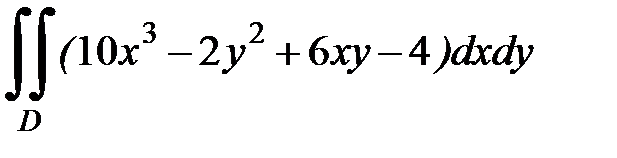 , D:
, D: 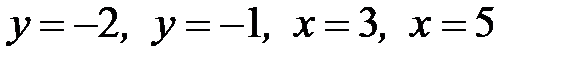 .
.
1.30. 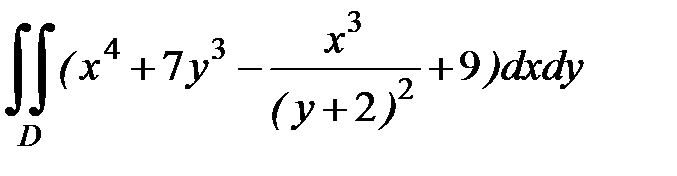 , D:
, D: 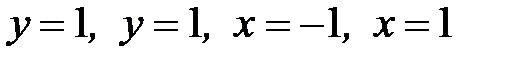 .
.
1.31. 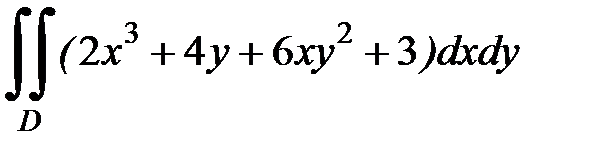 , D:
, D: 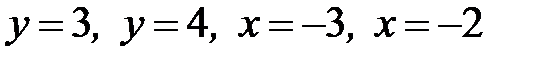
1.32. 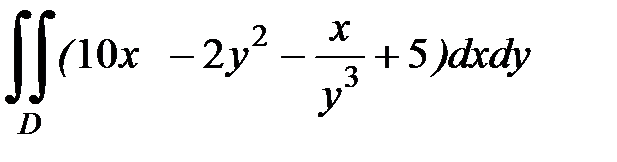 , D:
, D: 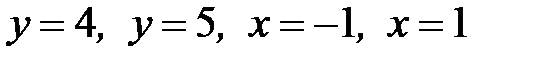 .
.
1.33. 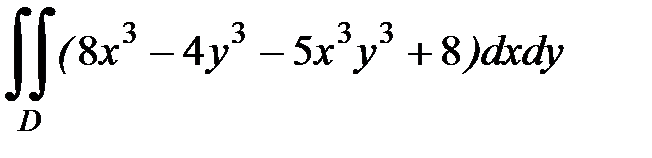 , D:
, D: 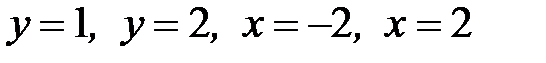 .
.
1.34. 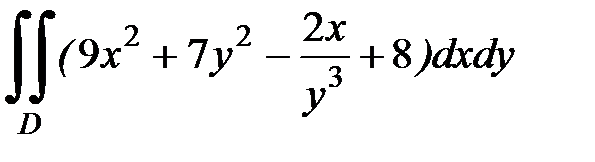 , D:
, D: 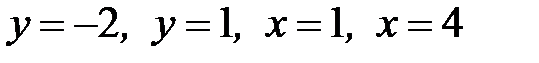 .
.
1.35. 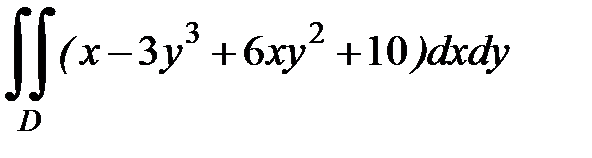 , D:
, D: 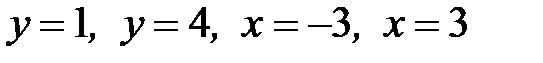 .
.
1.36. 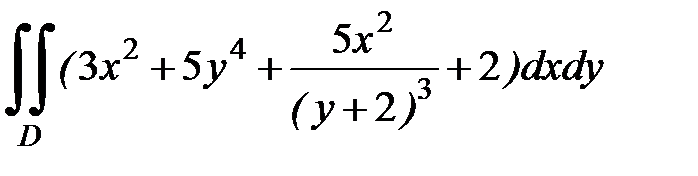 , D:
, D: 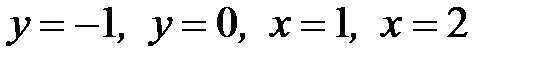 .
.
1.37. 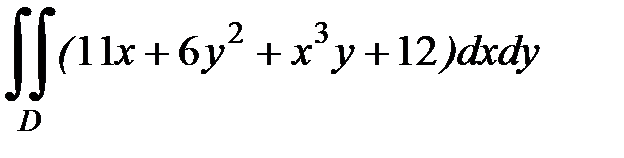 , D:
, D: 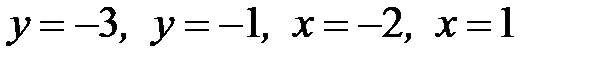 .
.
1.38. 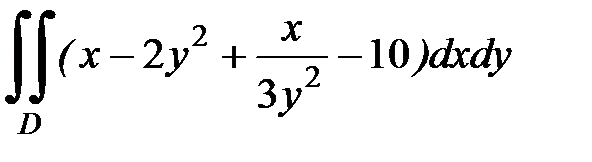 , D:
, D: 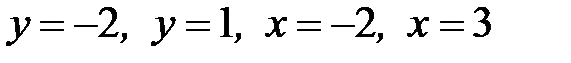 .
.
1.39. 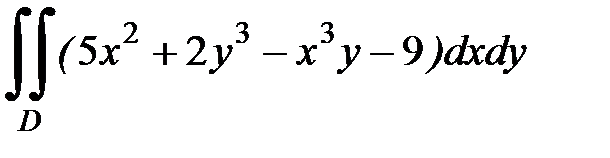 , D:
, D: 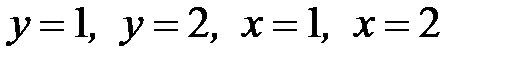 .
.
1.40. 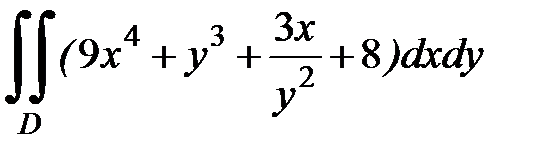 , D:
, D: 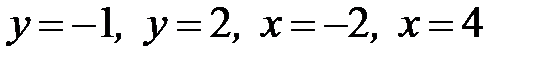 .
.
2. Вычислить двумя способами, поменяв порядок интегрирования, в виде двукратного или суммы двукратных интегралов. Изобразить область интегрирования :
|
|
|
2. 1. 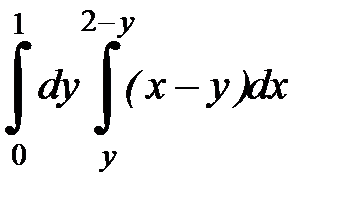
| 2.2. 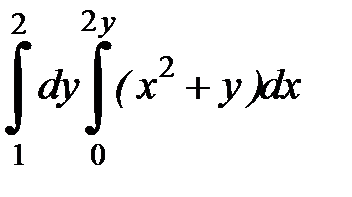
|
2.3. 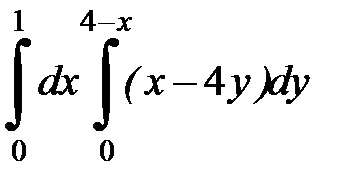
| 2. 4. 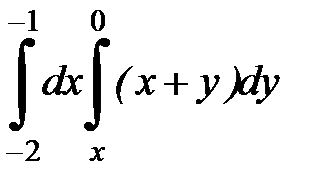
|
2. 5. 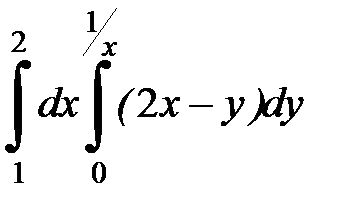
| 2. 6. 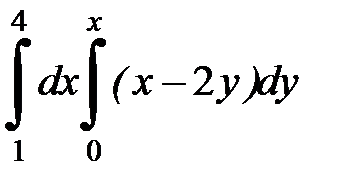
|
2. 7. 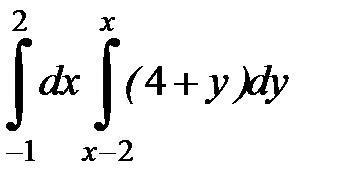
| 2. 8. 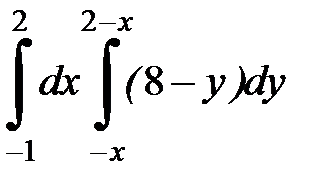
|
2. 9. 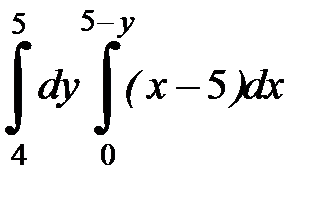
| 2. 10. 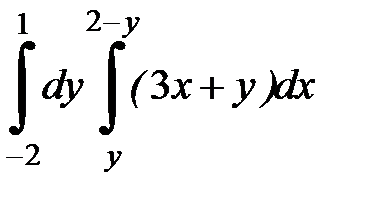
|
2. 11. 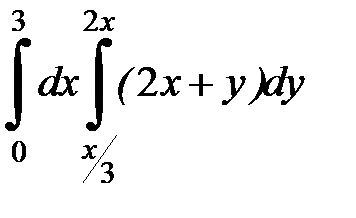
| 2. 12. 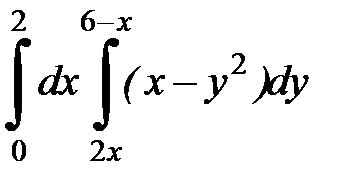
|
2. 13. 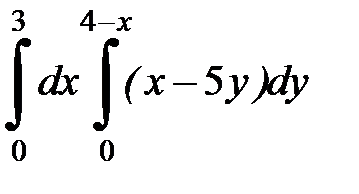
| 2. 14. 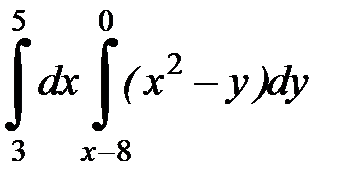
|
2. 15. 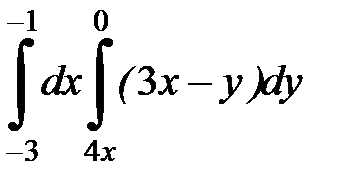
| 2. 16. 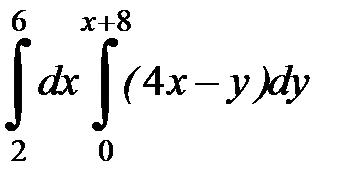
|
2. 17. 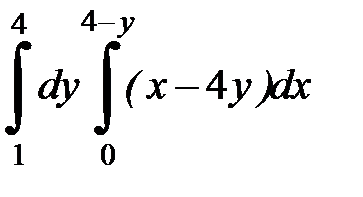
| 2. 18. 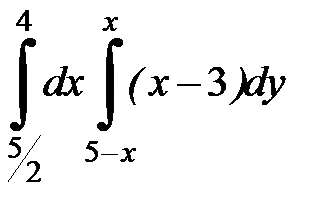
|
2. 19. 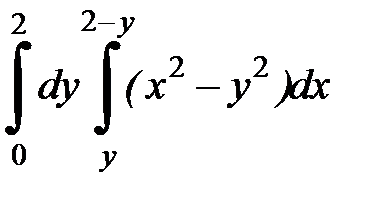
| 2. 20. 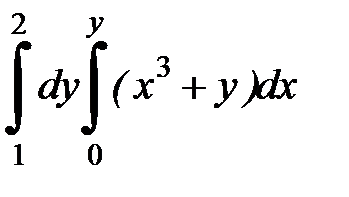
|
2. 21. 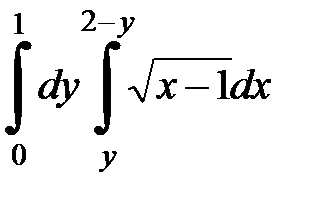
| 2. 22. 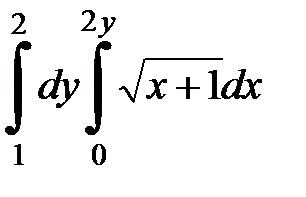
|
2. 23. 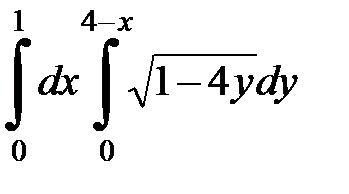
| 2. 24. 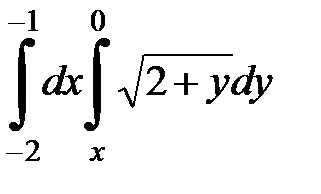
|
2.25. 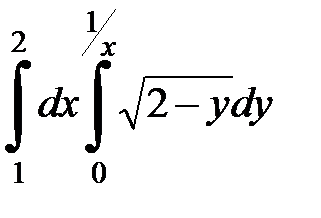
| 2.26. 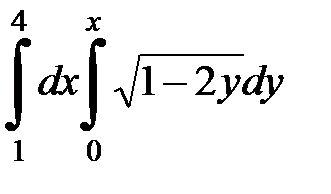
|
2.27. 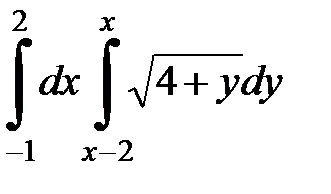
| 2.28. 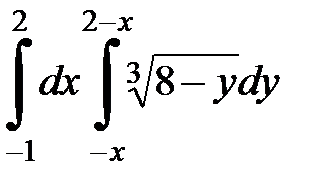
|
2.29. 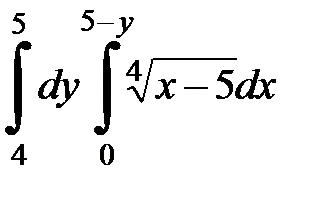
| 2.30. 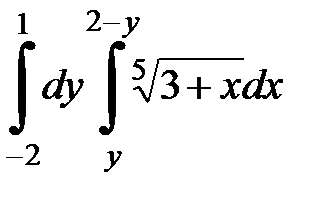
|
2.31. 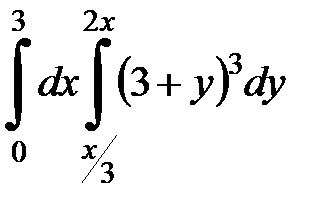
| 2.32. 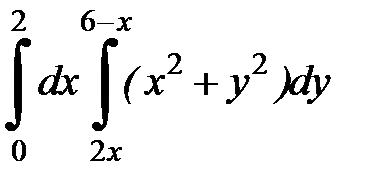
|
2.33. 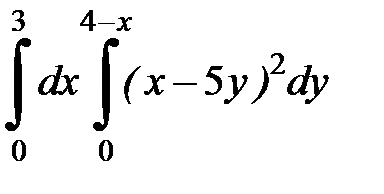
| 2.34. 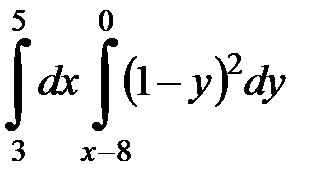
|
2.35. 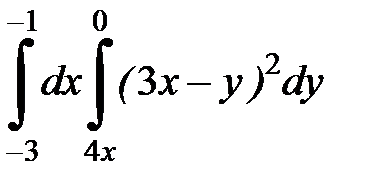
| 2.36. 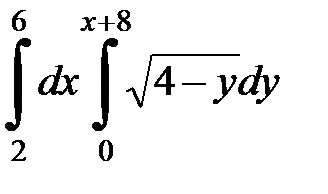
|
2.37. 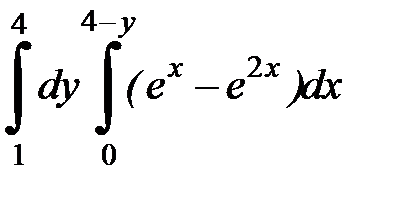
| 2.38. 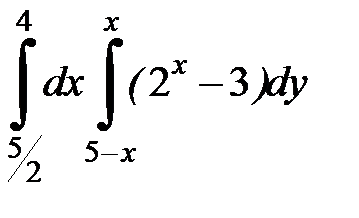
|
2.39. 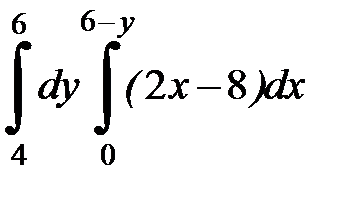
| 2.40. 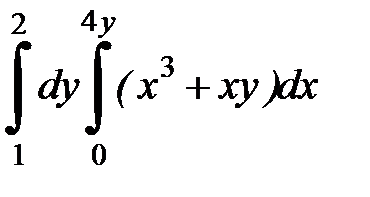
|
3. Вычислить двойной интеграл по области D , ограниченной указанными линиями, выбрав наиболее удобный путь интегрирования:
3.1. 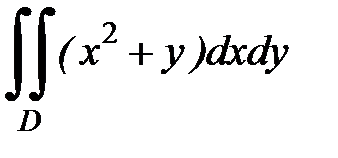 , D:
, D: 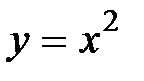 ,
, 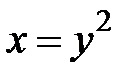 .
.
3.2. 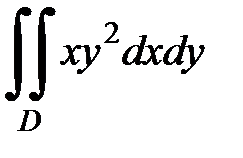 , D:
, D: 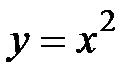 ,
, 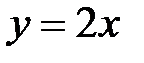 .
.
3.3. 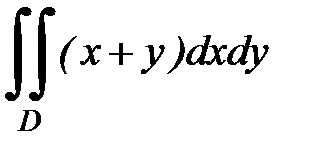 , D:
, D: 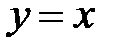 ,
, 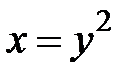 .
.
3.4. 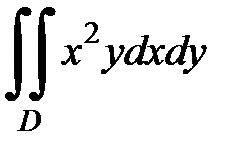 , D:
, D:  ,
, 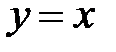 ,
, 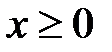 .
.
3.5. 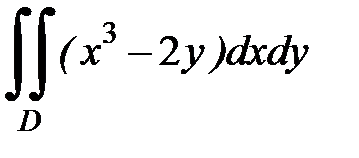 , D:
, D: 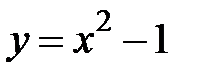 ,
, 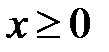 ,
, 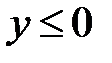 .
.
3.6. 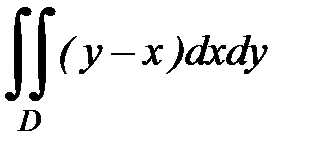 , D:
, D: 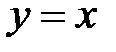 ,
,  .
.
3.7. 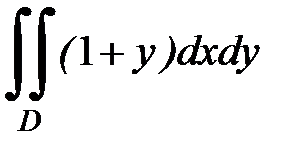 , D:
, D: 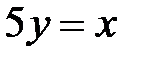 ,
, 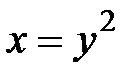 .
.
3.8. 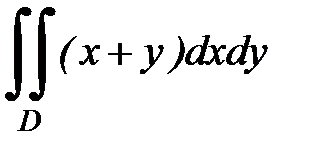 , D:
, D: 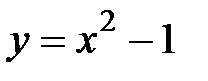 ,
, 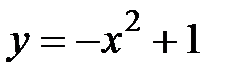 .
.
3.9. 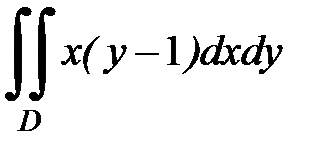 , D:
, D: 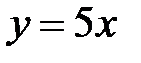 ,
, 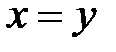 ,
, 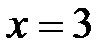 .
.
3.10. 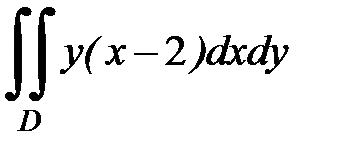 D:
D: 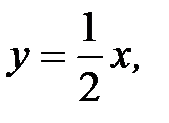
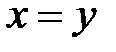 ,
, 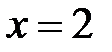
3.11. 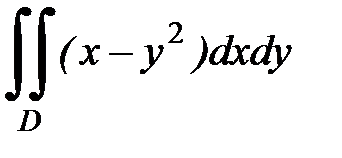 , D:
, D: 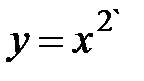 ,
, 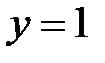 .
.
3.12. 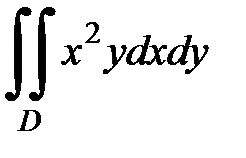 , D:
, D: 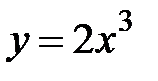 ,
, 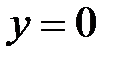 ,
, 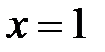
3.13. 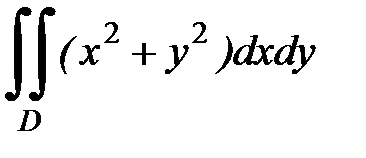 D:
D: 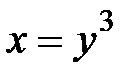 ,
, 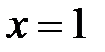 ,
, 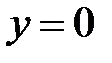
3.14. 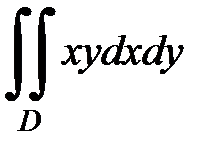 D:
D: 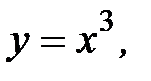
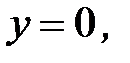
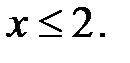
3.15. 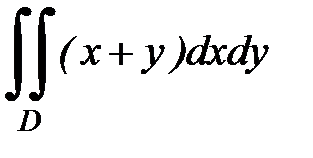 D:
D: 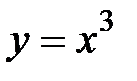 ,
, 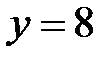 ,
, 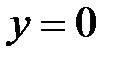 ,
, 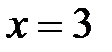 .
.
3.16. 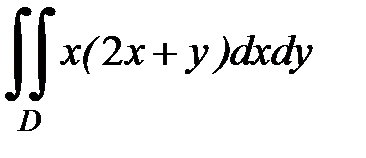 D:
D: 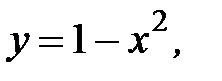
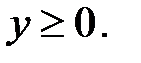
3.17. 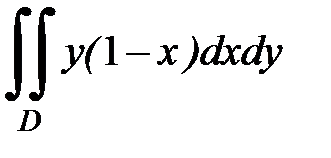 D:
D: 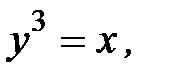
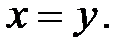
3.18. 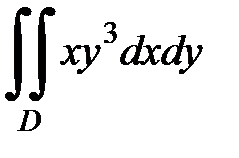 , D:
, D: 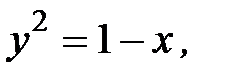
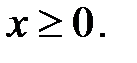
3.19. 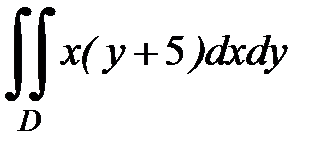 , D:
, D: 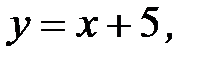
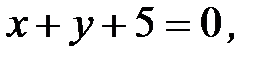
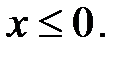
3.20. 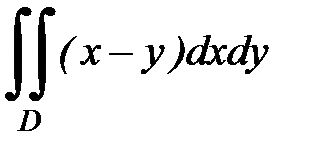 , D:
, D: 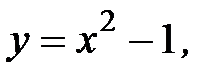
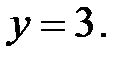
3.21. 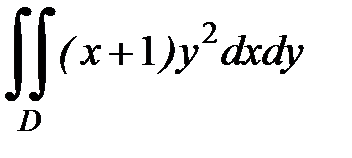 , D:
, D: 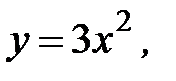
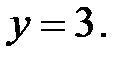
3.22. 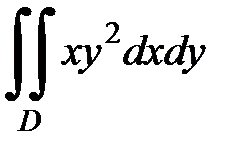 , D:
, D: 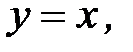
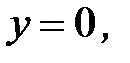
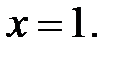
3.23. 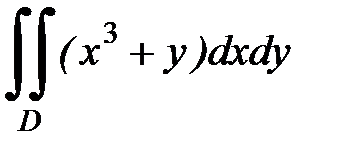 , D:
, D: 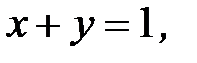
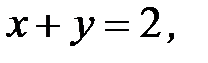
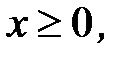
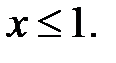
3.24. 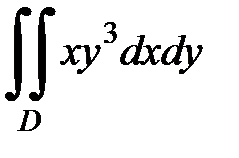 , D:
, D: 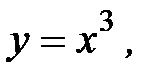
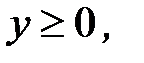
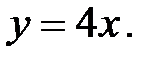
3.25. 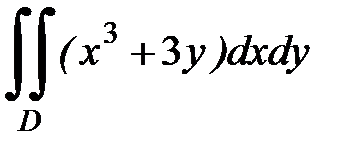 , D:
, D: 
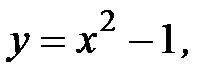
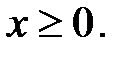
3.26. 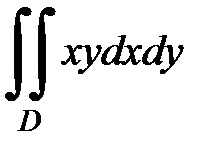 , D:
, D: 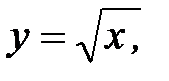
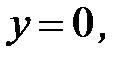
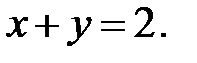
3.27. 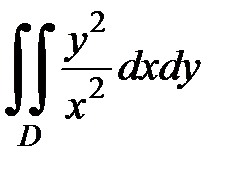 , D:
, D: 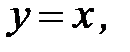
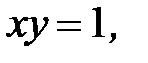
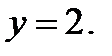
3.28. 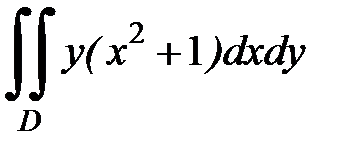 , D:
, D: 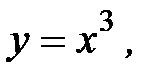
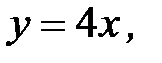
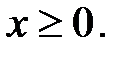
3.29. 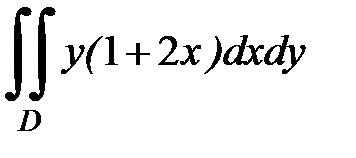 , D:
, D: 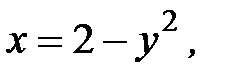
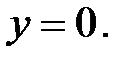
3.30. 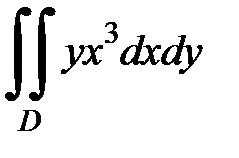 , D:
, D: 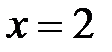 ,
, 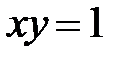 ,
, 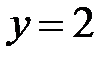 .
.
3.31.  D:
D: 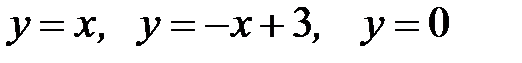 .
.
3.32. 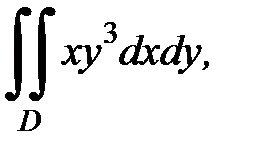 D:
D: 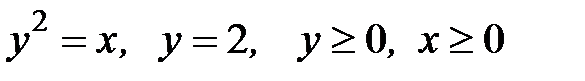 .
.
3.33. 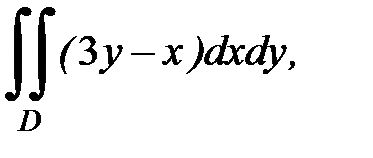 D:
D: 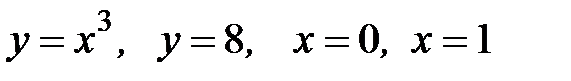 .
.
3.34. 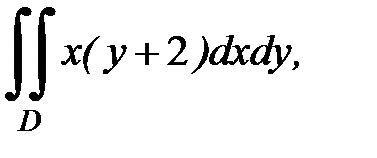 D:
D: 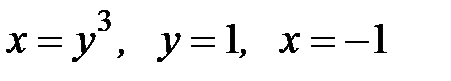 .
.
3.35. 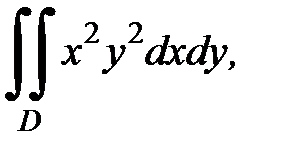 D:
D: 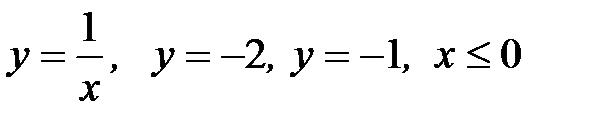 .
.
3.36. 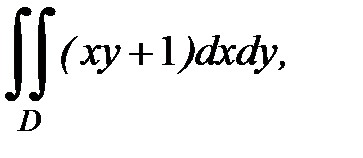 D:
D: 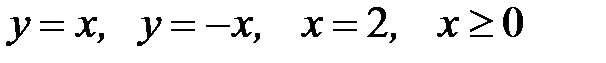 .
.
3.37. 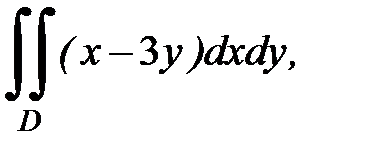 D:
D: 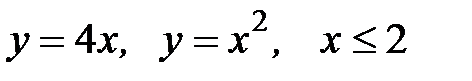
3.38. 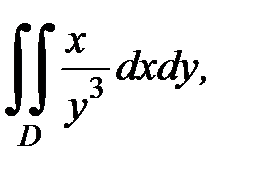 D:
D: 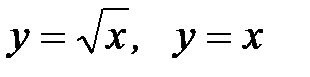 .
.
3.39. 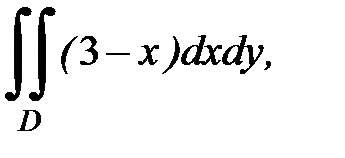 D:
D: 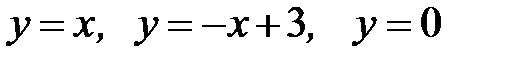
3.40. 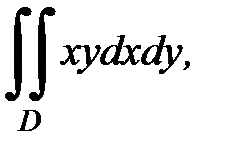 D:
D: 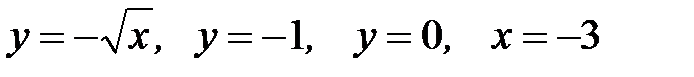
Вычислить двойной интеграл, перейдя к полярным координатам. Изобразить область интегрирования:
4. 1. 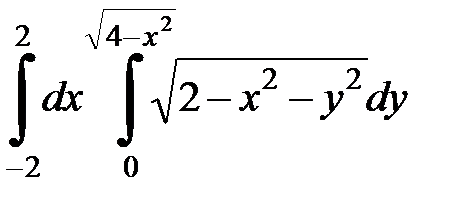
| 4.2. 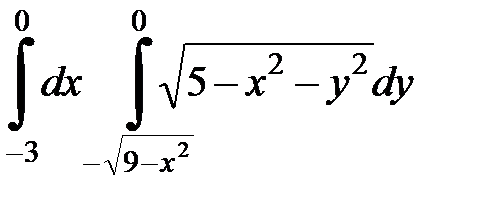
|
4.3. 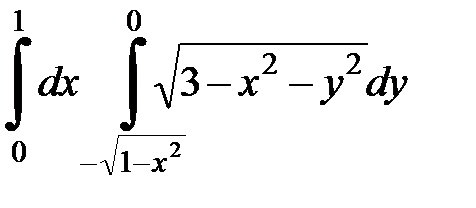
| 4. 4. 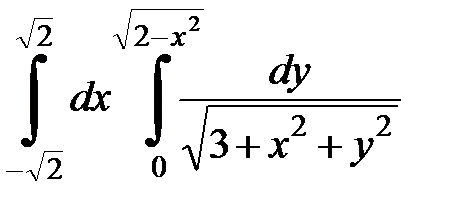
|
4. 5. 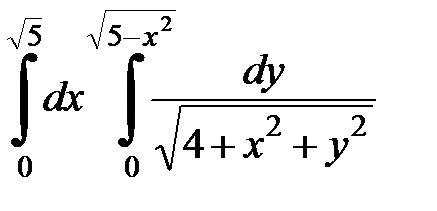
| 4. 6. 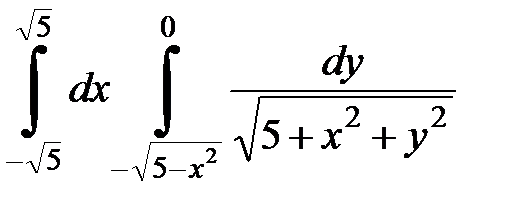
|
4. 7. 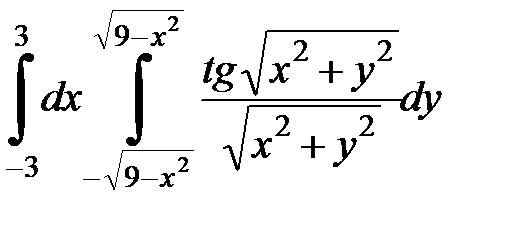
| 4. 8. 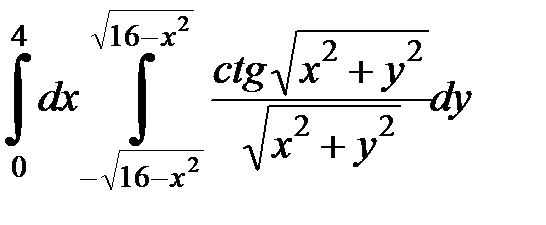
|
4 . 9. 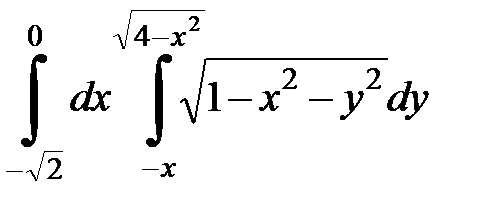
| 4 . 10. 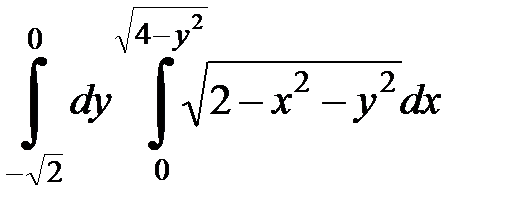
|
4. 11. 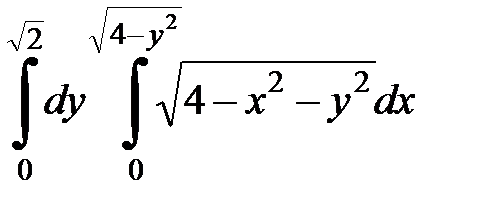
| 4 . 12. 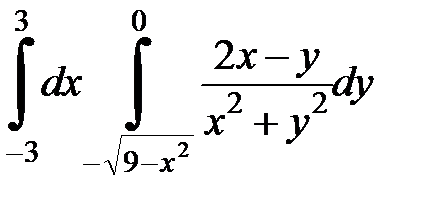
|
4. 13. 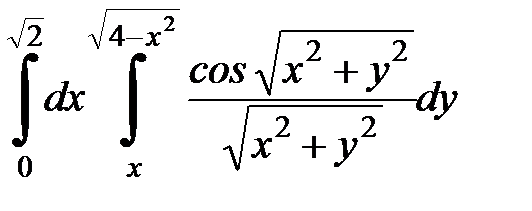
| 4. 14. 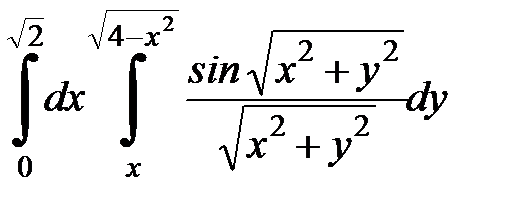
|
4. 15. 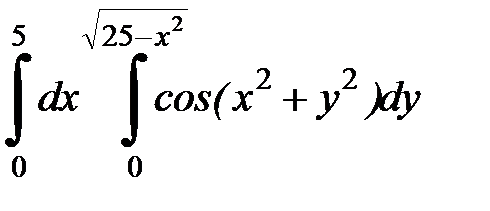
| 4. 16. 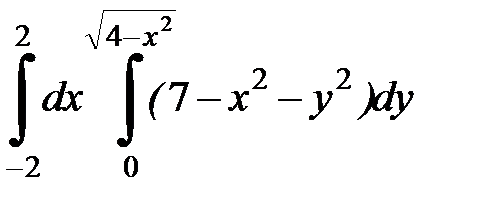
|
4. 17. 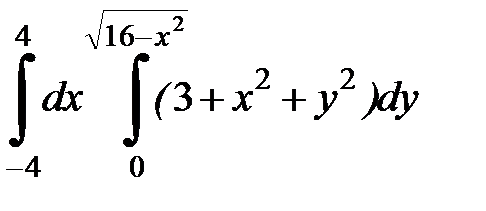
| 4. 18. 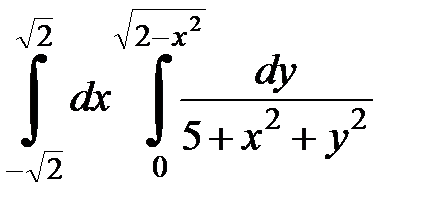
|
4. 19. 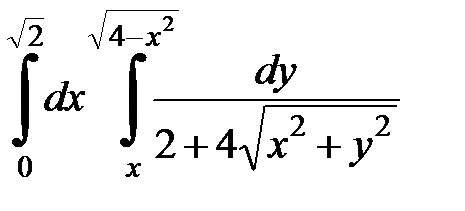
| 4. 20. 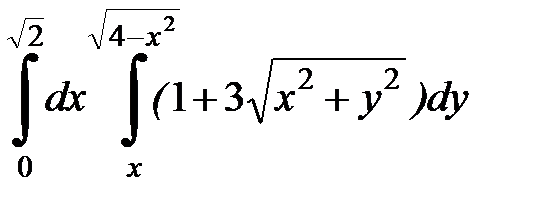
|
4. 21. 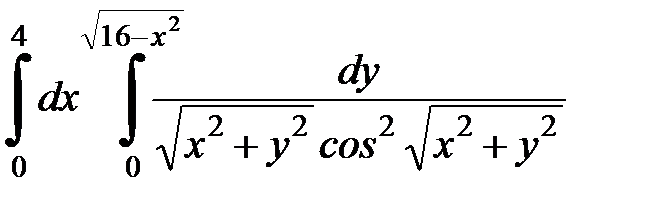
| 4. 22. 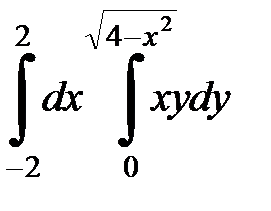
|
4. 23. 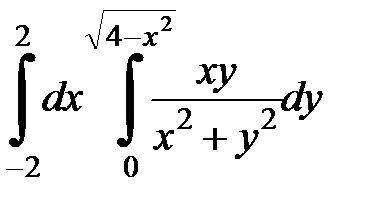
| 4. 24. 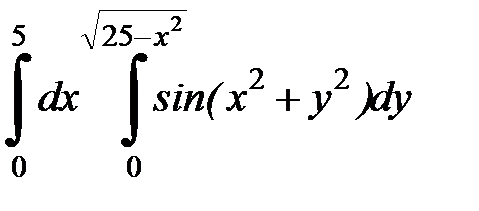
|
4.25. 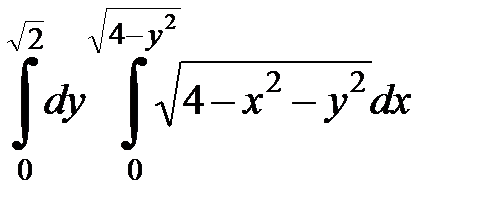
| 4.26. 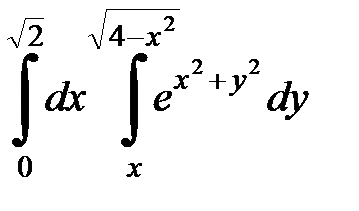
|
4.27. 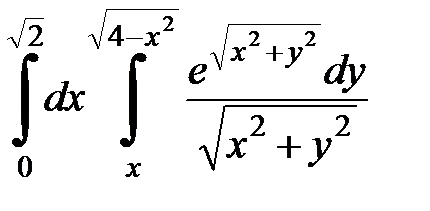
| 4.28. 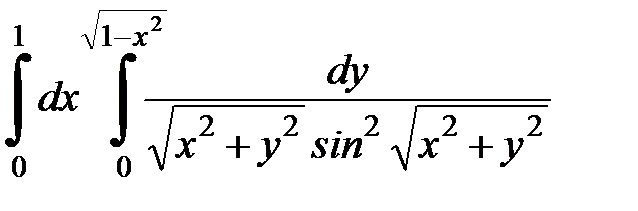
|
4.29. 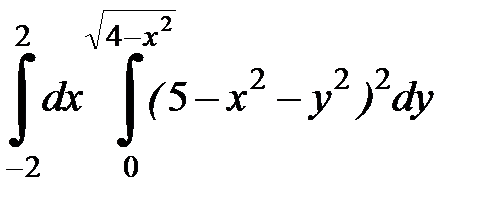
| 4.30. 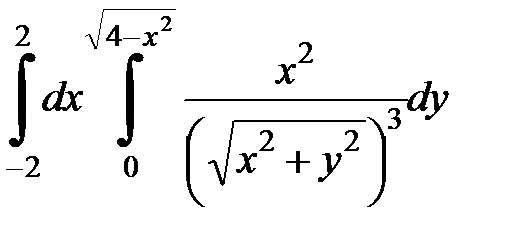
|
4.31. 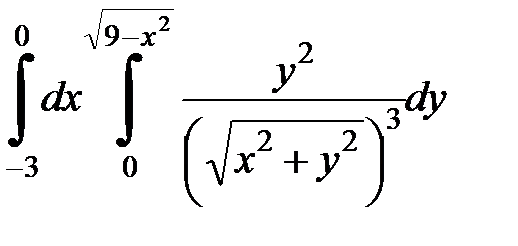
| 4.32. 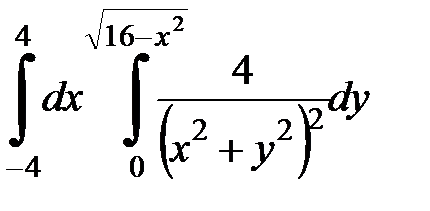
|
4.33. 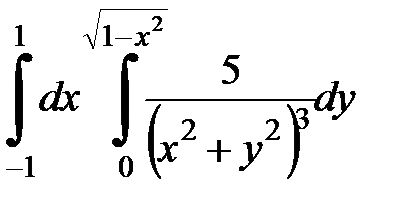
| 4.34. 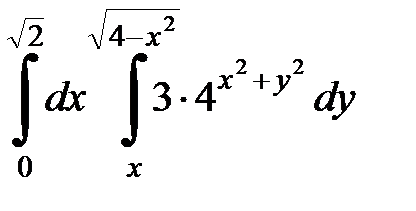
|
4.35. 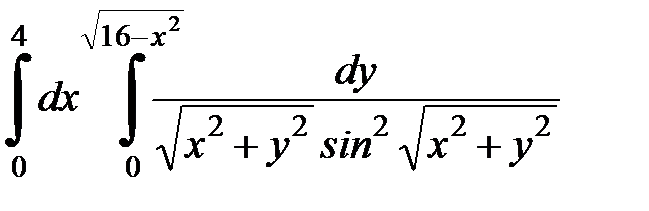
| 4.36. 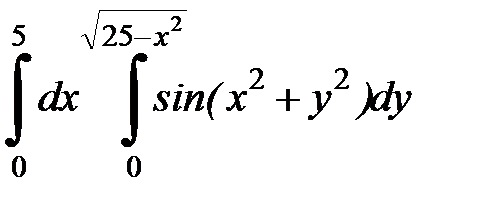
|
4.37. 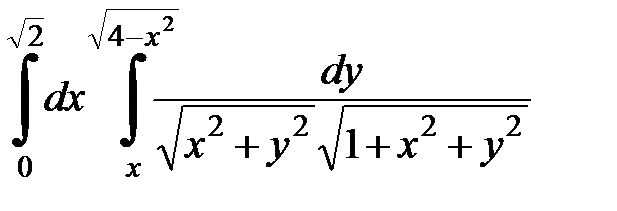
| 4.38. 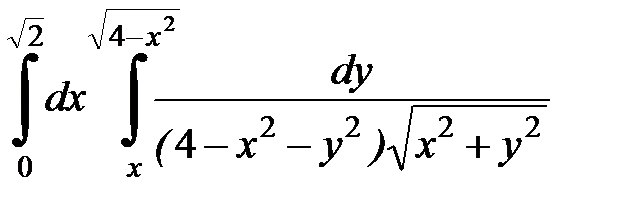
|
4.39. 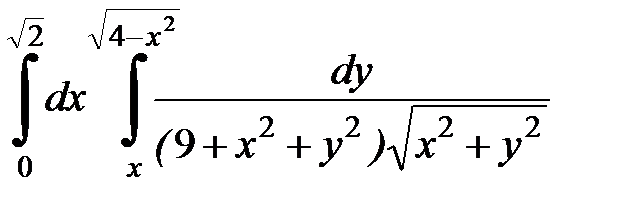
| 4.40. 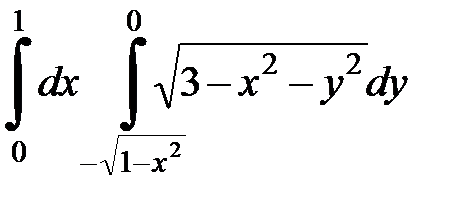
|
5. Вычислить площадь плоской области D , ограниченной заданными линиями. Изобразить область интегрирования :
5.1. 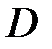 :
: 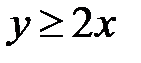 ,
, 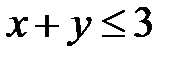 ,
, 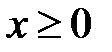 .
.
5.2.  :
: 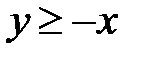 ,
, 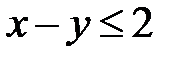 ,
, 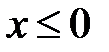 .
.
5.3.  :
: 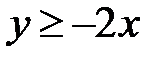 ,
, 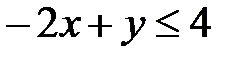 ,
, 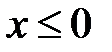 .
.
5.4.  :
: 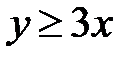 ,
, 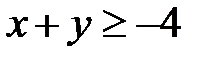 ,
, 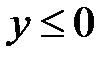 .
.
5.5.  :
: 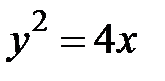 ,
, 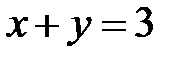 ,
, 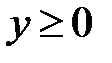 .
.
5. 6 .  :
: 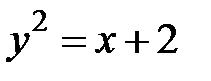 ,
, 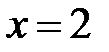 .
.
5. 7 .  :
: 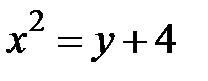 ,
, 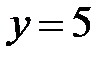 .
.
5. 8 .  :
: 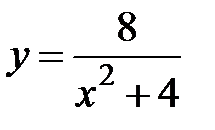 ,
, 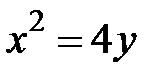 .
.
5. 9 .  :
: 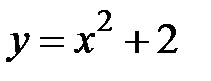 ,
, 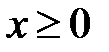 ,
, 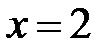 ,
, 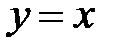 .
.
5. 10 .  :
: 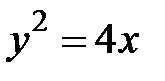 ,
, 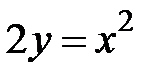 ,
, 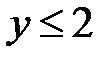 .
.
5.11.  :
: 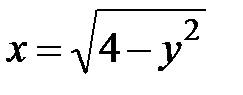 ,
, 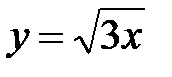 ,
, 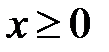 .
.
5. 12 .  :
: 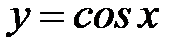 ,
, 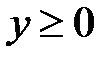 ,
, 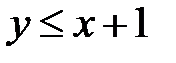 .
.
5. 13 .  :
: 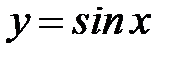 ,
, 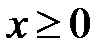 ,
, 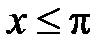 ,
, 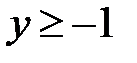 .
.
5. 14 .  :
: 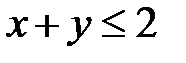 ,
, 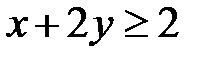 ,
, 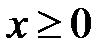 .
.
5.15.  :
: 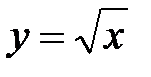 ,
, 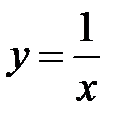 ,
, 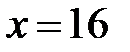 .
.
5.16.  :
: 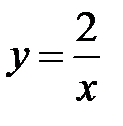 ,
, 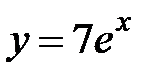 ,
, 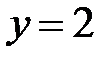 ,
, 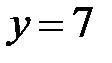 .
.
5.17.  :
: 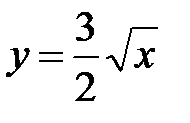 ,
, 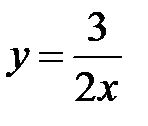 ,
, 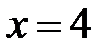 .
.
5.18.  :
: 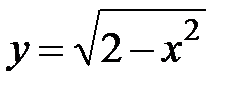 ,
, 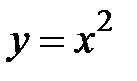 .
.
5.19.  :
: 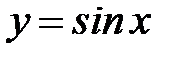 ,
, 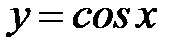 ,
, 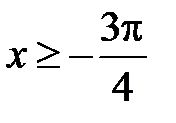 ,
, 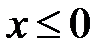 ,
,
5.20.  :
: 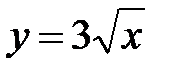 ,
, 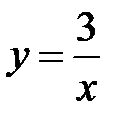 ,
, 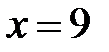 .
.
5.21.  :
: 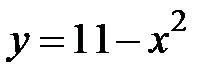 ,
, 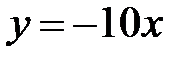 .
.
5.22.  :
: 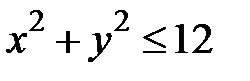 ,
,  .
.
5. 23 .  :
: 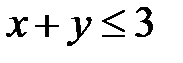 ,
, 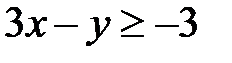 ,
, 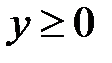 .
.
5. 24.  :
: 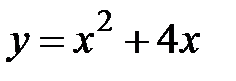 ,
, 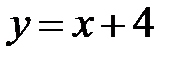 .
.
5. 25.  :
: 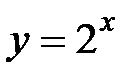 ,
, 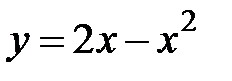 ,
, 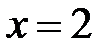 ,
, 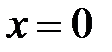 .
.
5. 25.  :
: 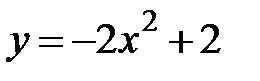 ,
, 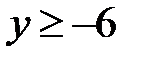 .
.
5. 26.  :
: 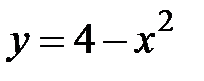 ,
, 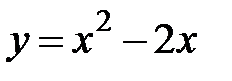 .
.
5. 27.  :
: 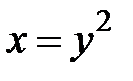 ,
, 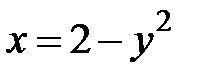 .
.
5. 28.  :
: 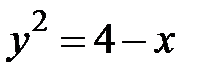 ,
, 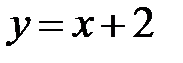 ,
, 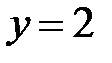 ,
, 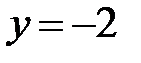 .
.
5.29.  :
: 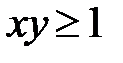 ,
, 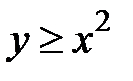 ,
, 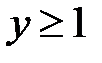 ,
, 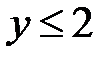 .
.
5.30.  :
: 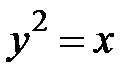 ,
, 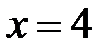 .
.
5.31.  :
: 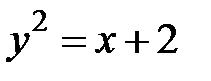 ,
, 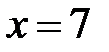 .
.
5.32.  :
: 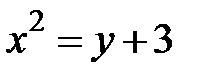 ,
, 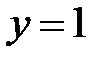 .
.
5.33.  :
: 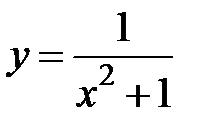 ,
, 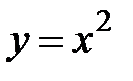 .
.
5.34.  :
: 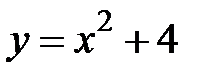 ,
, 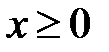 ,
, 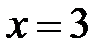 ,
, 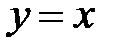 .
.
5.35.  :
: 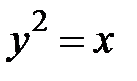 ,
, 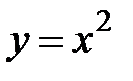 .
.
5.36.  :
: 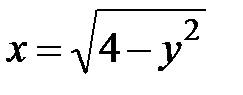 ,
, 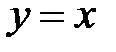 ,
, 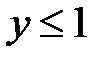 .
.
5.37.  :
: 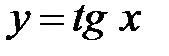 ,
, 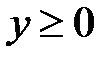 ,
, 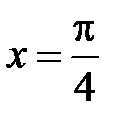 .
.
5.38.  :
: 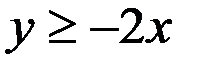 ,
, 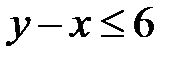 ,
, 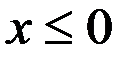 .
.
5.39.  :
: 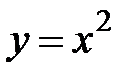 ,
, 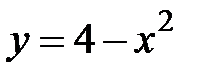 .
.
5.40.  :
: 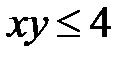 ,
, 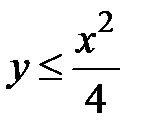 ,
, 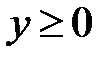 ,
, 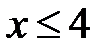 .
.
6. Вычислить объем тела, ограниченного заданными поверхностями:
6.1. 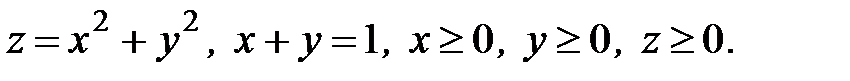
6.2. 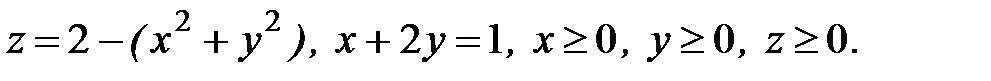
6.3. 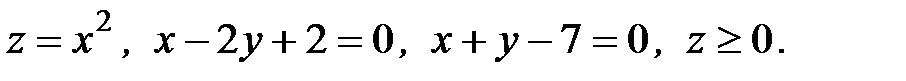
6.4. 
6.5. 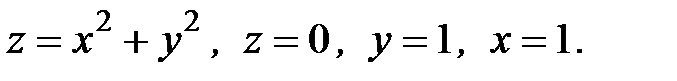
6.6. 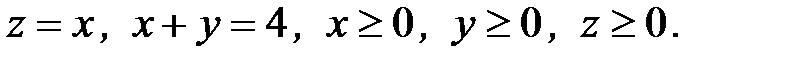
6.7. 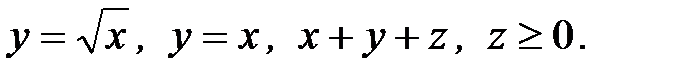
6.8. 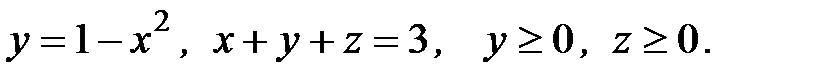
6.9. 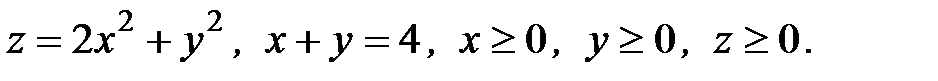
6.10. 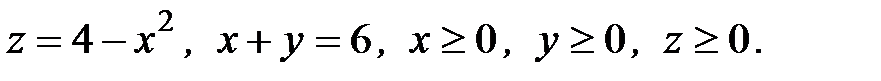
6.11. 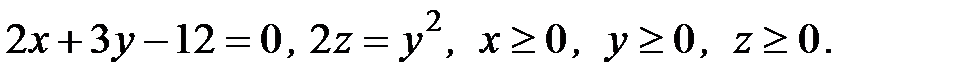
6.12. 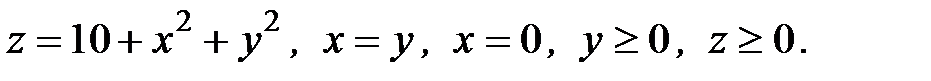
6.13. 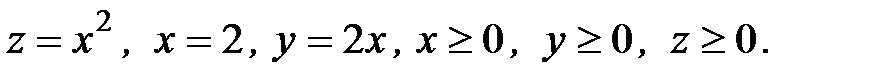
6.14. 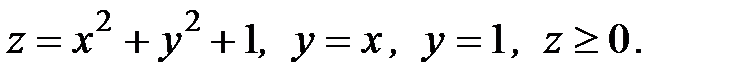
6.15. 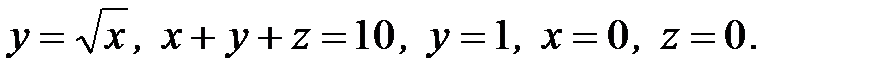
6.16. 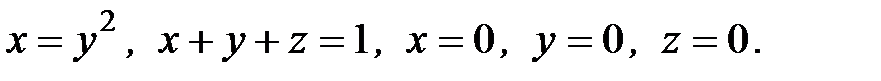
6.17. 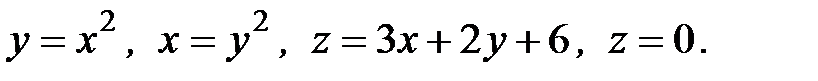
6.18. 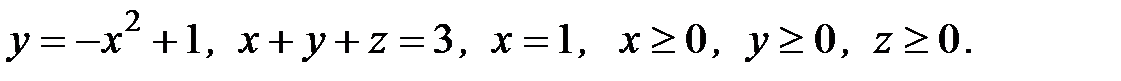
6.19. 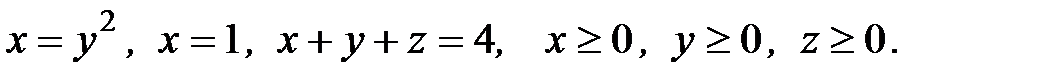
6.20. 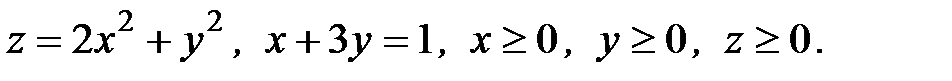
6.21. 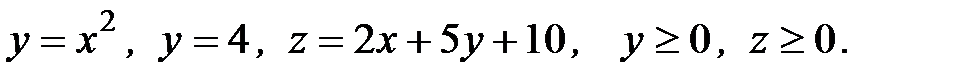
6.22. 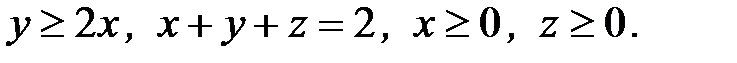
6.23. 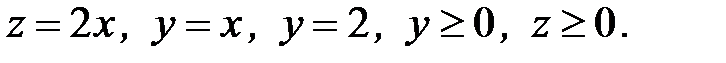
6.24. 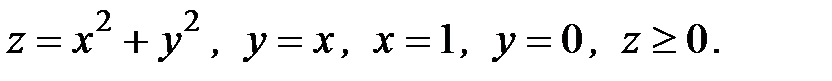
6.25. 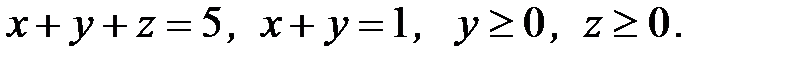
6.26. 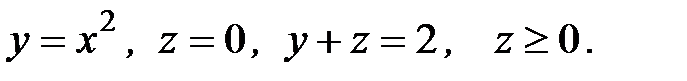
6.27. 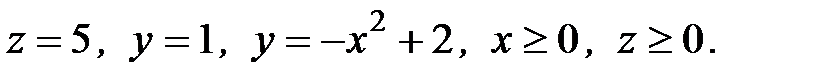
6.28. 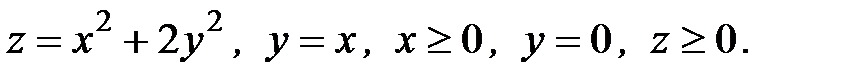
6.29. 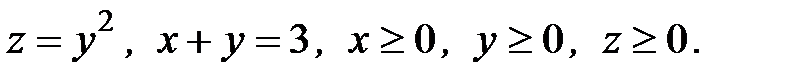
6.30. 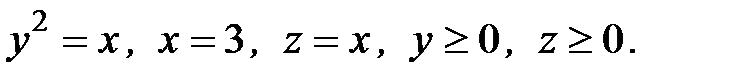
6.31. 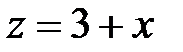 ,
, 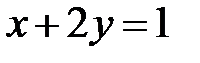 ,
, 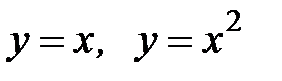 ,
, 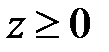 .
.
6.32. 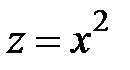 ,
, 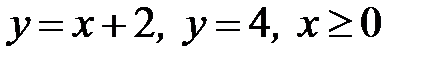 ,
, 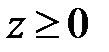 .
.
6.33. 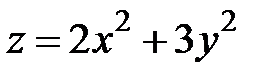 ,
, 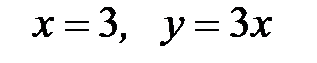 ,
, 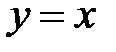 ,
, 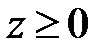 .
.
6.34. 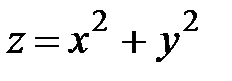 ,
, 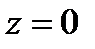 ,
, 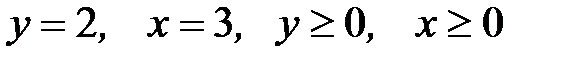 .
.
6.35. 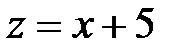 ,
, 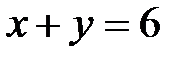 ,
, 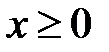 ,
, 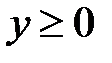 ,
, 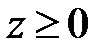 .
.
6.36. 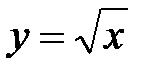 ,
, 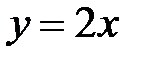 ,
, 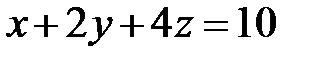 ,
, 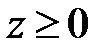 .
.
6.37. 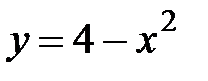 ,
, 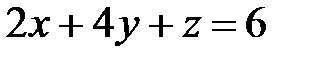
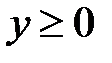 ,
, 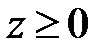 ,
, 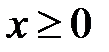 .
.
6.38. 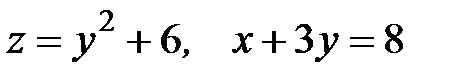 ,
, 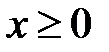 ,
, 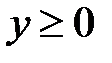 ,
, 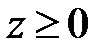 .
.
6.39. 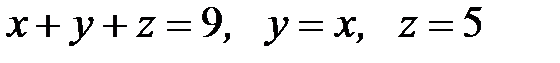 ,
, 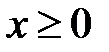 ,
, 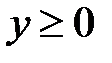 ,
, 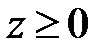 .
.
6.40. 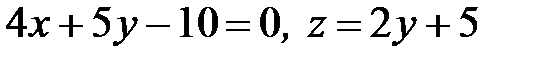
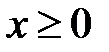 ,
, 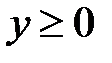 ,
, 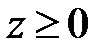 .
.
7. Вычислить криволинейный интеграл 1-го рода:
7.1. 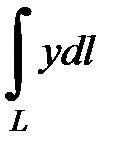 где
где 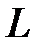 - дуга параболы
- дуга параболы 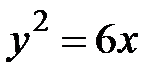 , отсеченная параболой
, отсеченная параболой 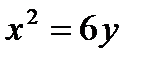 .
.
7.2. 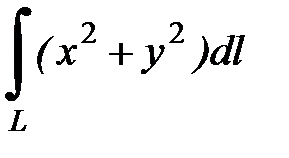 где
где 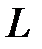 - первая четверть окружности
- первая четверть окружности 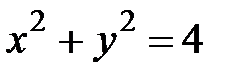 .
.
7.3. 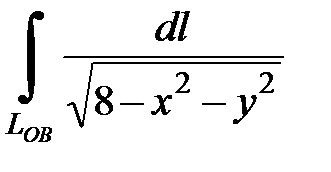 , где
, где 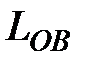 - отрезок прямой, соединяющий точки
- отрезок прямой, соединяющий точки 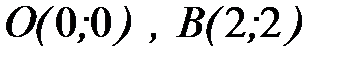 .
.
7.4. 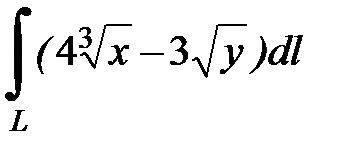 , где
, где 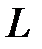 - отрезок прямой
- отрезок прямой 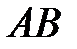 :
: 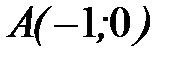 ;
; 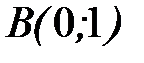 .
.
7.5. 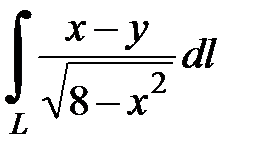 , где
, где 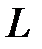 - отрезок прямой, заключенный между точками
- отрезок прямой, заключенный между точками 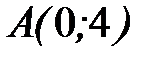 и
и 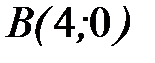 .
.
7.6. 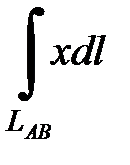 , где
, где 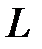 - дуга параболы
- дуга параболы 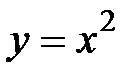 от точки
от точки 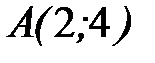 до точки
до точки 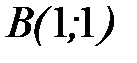 .
.
7.7. 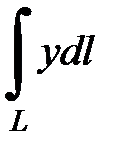 , где
, где 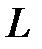 - дуга астроиды
- дуга астроиды 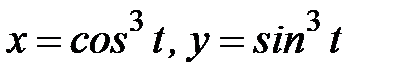 , при
, при 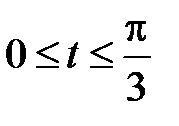 .
.
7.8. 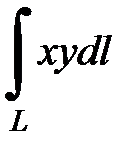 где
где 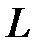 - прямая от точки О(0;0) до точки А(4;2).
- прямая от точки О(0;0) до точки А(4;2).
7.9. 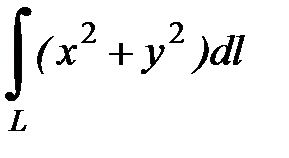 , где
, где 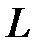 - дуга кривой
- дуга кривой 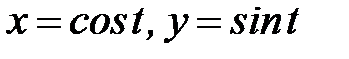 ,
, 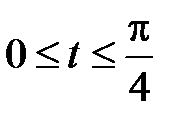 .
.
7.10. 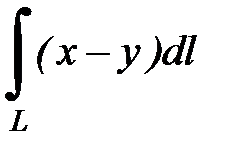 , где
, где 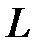 - верхняя половина окружности
- верхняя половина окружности 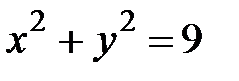 .
.
7.11. 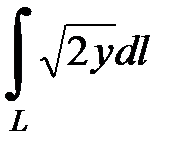 где
где 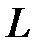 - часть циклоиды
- часть циклоиды 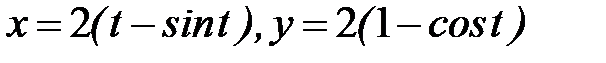 , при
, при 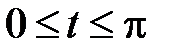
7.12. 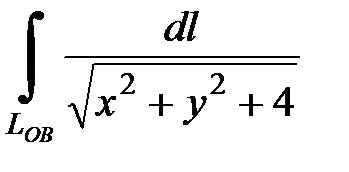 где
где 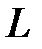 - отрезок прямой, соединяющий точки: О(0;0) ; B(1;2).
- отрезок прямой, соединяющий точки: О(0;0) ; B(1;2).
7.13. 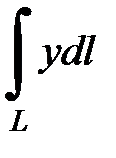 , где
, где 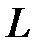 - дуга параболы
- дуга параболы 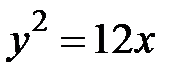 , отсеченная параболой
, отсеченная параболой 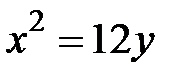 .
.
7.14. 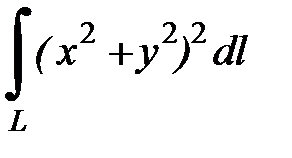 , где
, где 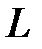 - третья четверть окружности
- третья четверть окружности 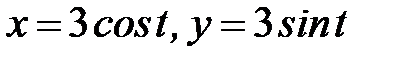 .
.
7.15. 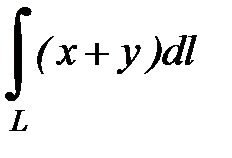 , где
, где 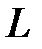 - прямая от точки
- прямая от точки 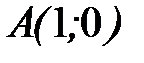 до точки
до точки 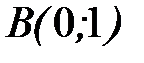 и от точки
и от точки 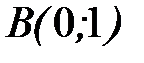 до точки
до точки 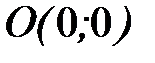 .
.
7.16. 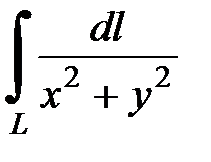 где
где 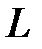 - часть кривой
- часть кривой 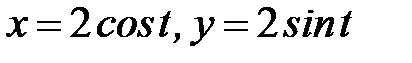 ,
, 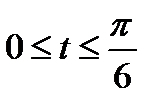 .
.
7.17. 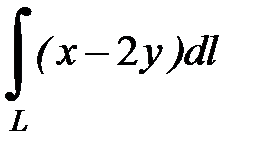 , где
, где 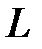 - прямая от точки
- прямая от точки 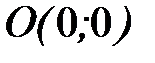 до точки
до точки 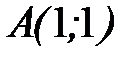 и от точки
и от точки 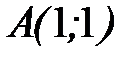 до точки
до точки 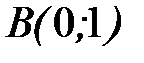 .
.
7.18. 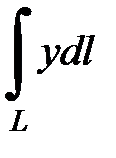 , где
, где 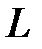 - дуга кривой
- дуга кривой 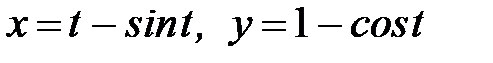 ,
, 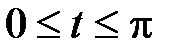 .
.
7.19. 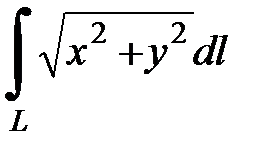 где
где 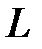 - вторая четверть окружности
- вторая четверть окружности 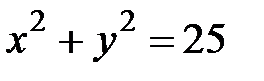 .
.
7.20. 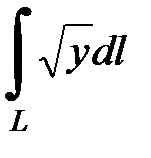 , где
, где 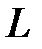 - первая арка циклоиды
- первая арка циклоиды 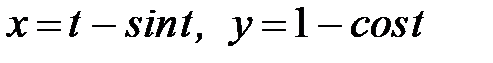 ,
, 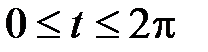 .
.
7.21. 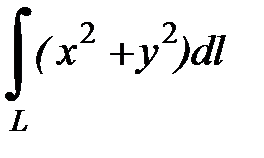 , где
, где 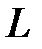 - нижняя половина окружности
- нижняя половина окружности 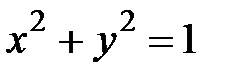 .
.
7.22. 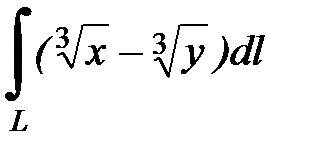 , где
, где 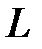 - дуга астроиды
- дуга астроиды 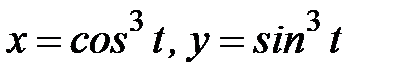 , при
, при 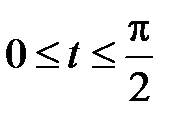 .
.
7.23. 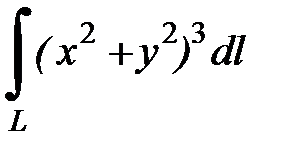 , где
, где 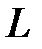 - первая четверть окружности
- первая четверть окружности 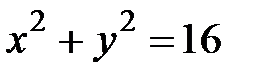 .
.
7.24. 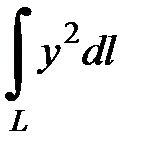 , где
, где 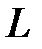 - первая арка циклоиды
- первая арка циклоиды 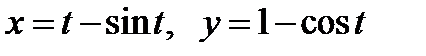 ,
, 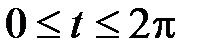 .
.
7.25. 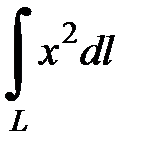 , где
, где 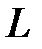 - верхняя половина окружности
- верхняя половина окружности 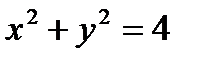 .
.
7.26. 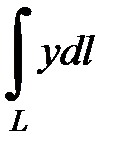 , где
, где 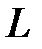 - дуга параболы
- дуга параболы 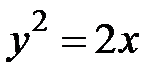 , отсеченная параболой
, отсеченная параболой 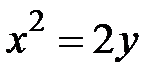 .
.
7.27. 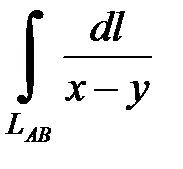 где
где 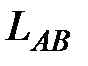 - отрезок прямой, заключенный между точками
- отрезок прямой, заключенный между точками 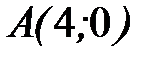 ;
; 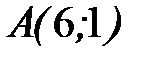 .
.
7.28. 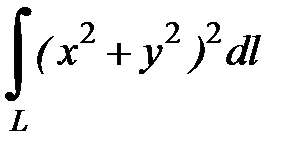 , где
, где 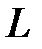 - четвертая четверть окружности
- четвертая четверть окружности 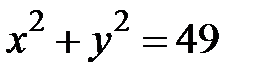 .
.
7.29. 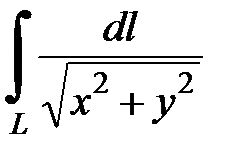 где
где 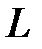 - отрезок прямой, соединяющий точки
- отрезок прямой, соединяющий точки 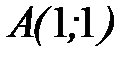 и
и 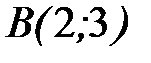 .
.
7.30. 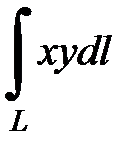 где
где 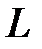 - дуга параболы
- дуга параболы 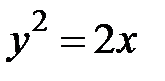 , отсеченная параболой
, отсеченная параболой 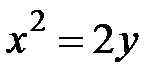 .
.
7.31. 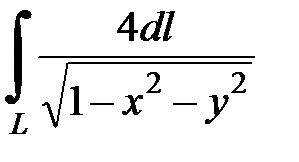 где L - отрезок прямой, соединяющий точки
где L - отрезок прямой, соединяющий точки 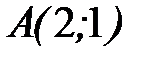 и
и 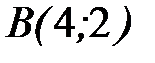 .
.
7.32. 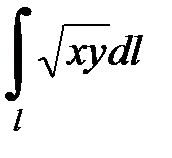 где L - отрезок прямой
где L - отрезок прямой 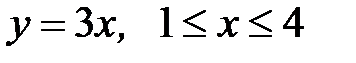 .
.
7.33. 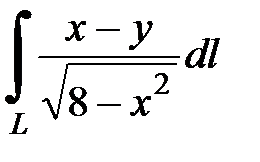 , где
, где 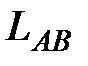 - отрезок прямой, заключенный между точками
- отрезок прямой, заключенный между точками 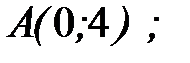
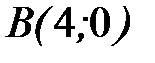
7.34. 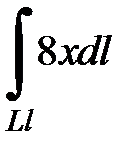 где L- дуга параболы
где L- дуга параболы 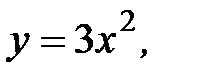 от точки
от точки 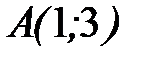 до точки
до точки 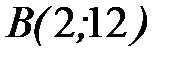 .
.
7.35. 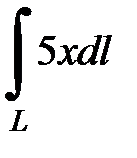 , где L- часть кривой
, где L- часть кривой 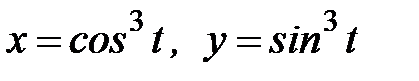 при
при 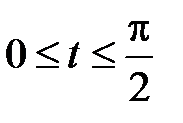 .
.
7.36. 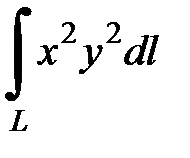 где L - прямая от точки
где L - прямая от точки 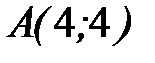 до точки
до точки 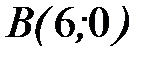 .
.
7.37. 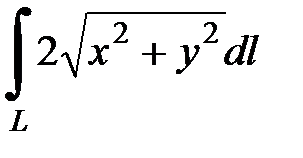 , где
, где 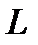 - дуга кривой
- дуга кривой 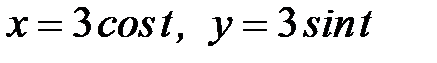 ,
, 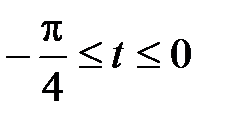 .
.
7.38. 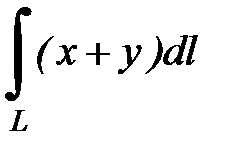 , где
, где 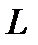 -левая половина окружности
-левая половина окружности 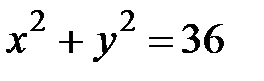 .
.
7.39. 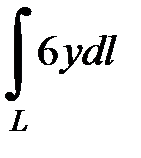 , где
, где 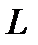 - часть циклоиды
- часть циклоиды 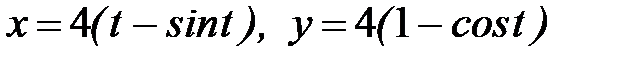 при
при 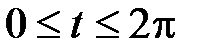
7.40. 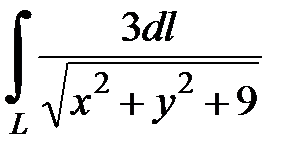 , где L - отрезок прямой от точки
, где L - отрезок прямой от точки 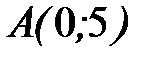 до точки
до точки 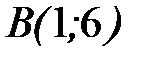 .
.
Задание 8. Вычислить данный криволинейный интеграл II рода:
8.1. 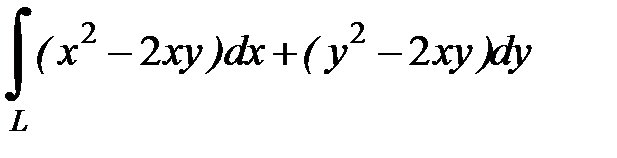 , где
, где 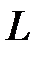 - дуга параболы
- дуга параболы 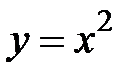 от точки
от точки 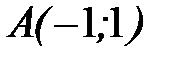 до точки
до точки 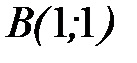 .
.
8.2. 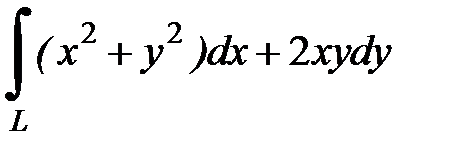 , где
, где  - дуга кубической параболы
- дуга кубической параболы 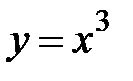 от точки
от точки 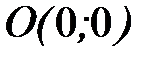 до точки
до точки 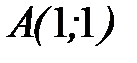 .
.
8.3. 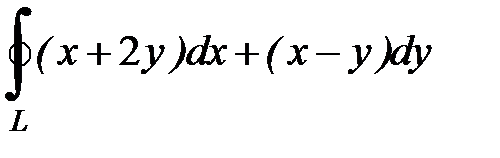 , где
, где  - окружность
- окружность 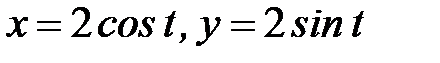 при положительном направлении обхода.
при положительном направлении обхода.
8.4. 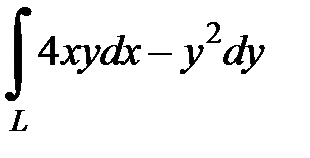 , где
, где 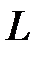 - ломаная
- ломаная 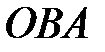 ;
; 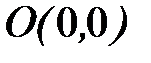 ;
; 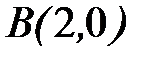 ;
; 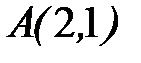 .
.
8.5. 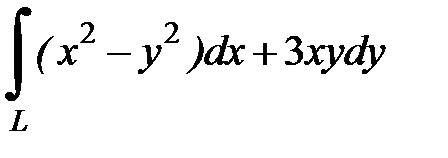 , где
, где 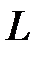 - отрезок прямой
- отрезок прямой 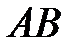 от точки
от точки 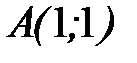 до точки
до точки 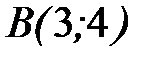 .
.
8.6. 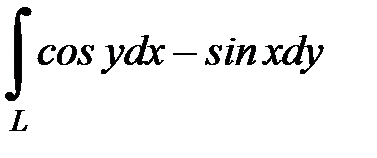 , где
, где 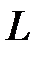 - отрезок прямой
- отрезок прямой 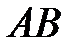 от точки
от точки 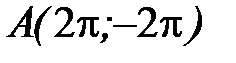 до точки
до точки 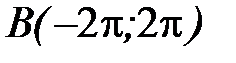 .
.
8.7. 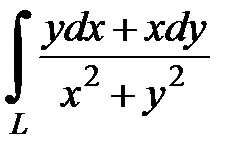 , где
, где 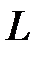 - отрезок прямой
- отрезок прямой 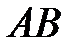 от точки
от точки 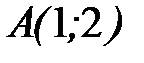 до точки
до точки 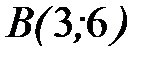 .
.
8.8. 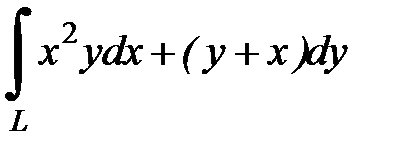 , где
, где  - дуга кубической параболы
- дуга кубической параболы 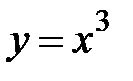 от точки
от точки 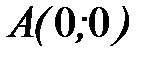 до точки
до точки 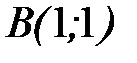 .
.
8.9.  , где
, где 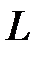 - ломаная
- ломаная 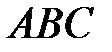 ;
;  ;
; 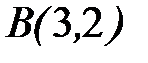 ;
; 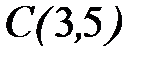 .
.
8.10. 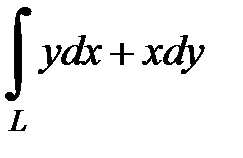 , где
, где  - дуга окружности
- дуга окружности 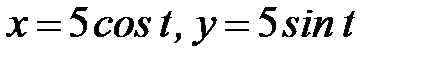 от точки
от точки 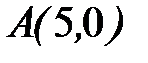 до точки
до точки 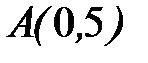 .
.
8.11. 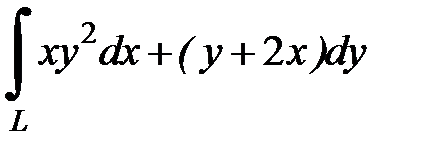 , где
, где  - дуга параболы
- дуга параболы 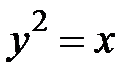 от точки
от точки 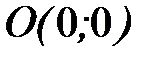 до точки
до точки 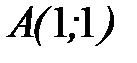 .
.
8.12. 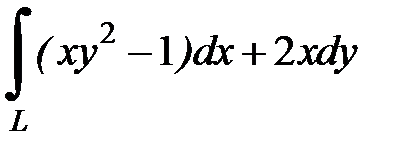 , где
, где  - дуга параболы
- дуга параболы 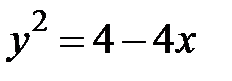 от точки
от точки 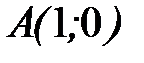 до точки
до точки 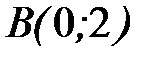 .
.
8.13. 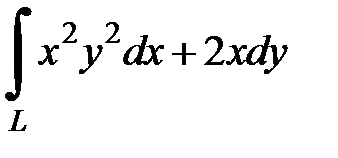 , где
, где  - дуга параболы
- дуга параболы 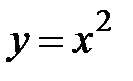 от точки
от точки 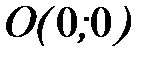 до точки
до точки 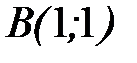 .
.
8.14. 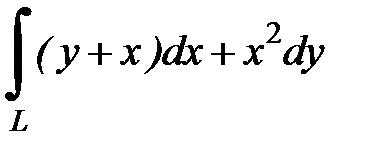 , где
, где  - дуга фигуры Лиссажу
- дуга фигуры Лиссажу 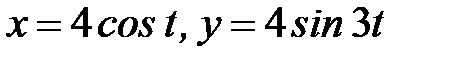 от точки
от точки 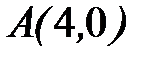 до точки
до точки 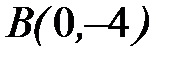 .
.
8.15. 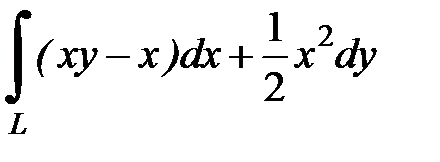 , где
, где  - дуга параболы
- дуга параболы 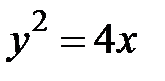 от точки
от точки 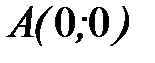 до точки
до точки 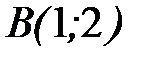 .
.
8.16. 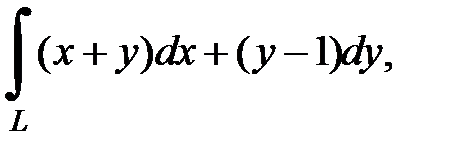 где
где  - дуга параболы, заданной параметрически
- дуга параболы, заданной параметрически 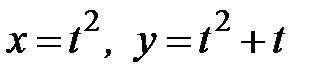 от точки
от точки 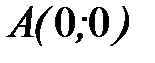 до точки
до точки 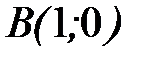 .
.
8.17. 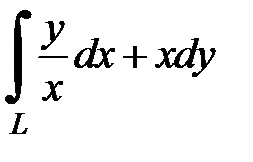 , где
, где  - дуга линии
- дуга линии 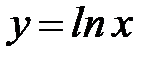 от точки
от точки 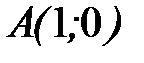 до точки
до точки 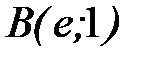 .
.
8.18 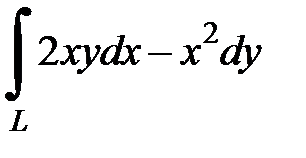 , где
, где  - дуга параболы
- дуга параболы 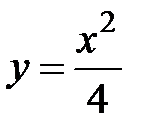 от точки
от точки 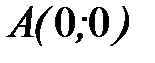 до точки
до точки 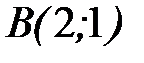 .
.
8.19. 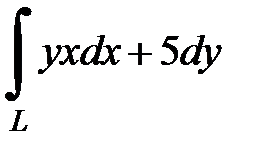 , где
, где  - дуга окружности
- дуга окружности 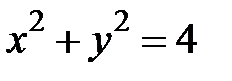 от точки
от точки 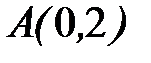 до точки
до точки 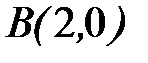 .
.
8.20. 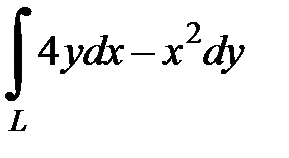 , где
, где  - дуга гиперболы
- дуга гиперболы 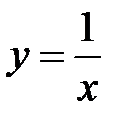 от точки
от точки 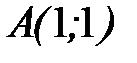 до точки
до точки 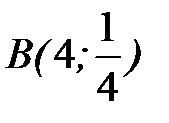 .
.
8.21. 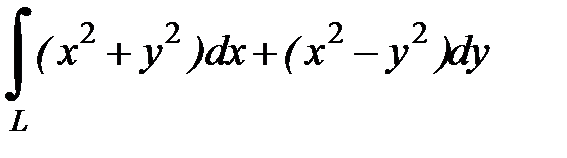 , где
, где 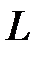 - ломаная линия
- ломаная линия 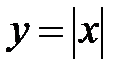 от точки
от точки 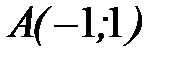 до точки
до точки 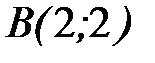 .
.
8.22. 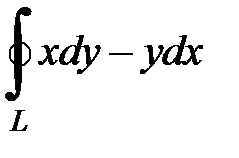 , где
, где  - контур треугольника с вершинами
- контур треугольника с вершинами 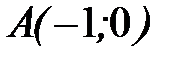 ,
, 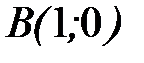 ,
, 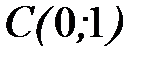 при положительном направлении обхода.
при положительном направлении обхода.
8.23. 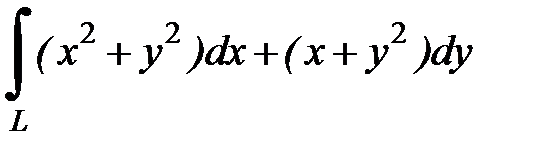 , где
, где 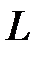 - ломаная
- ломаная 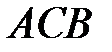 ;
; 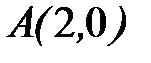 ;
; 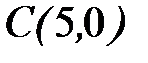 ;
; 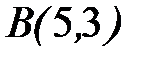 .
.
8.24. 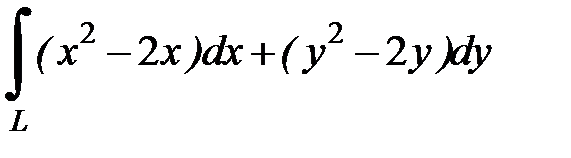 , где
, где 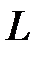 - дуга параболы
- дуга параболы 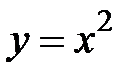 от точки
от точки 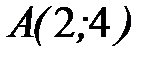 до точки
до точки 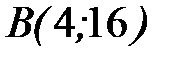 .
.
8.25. 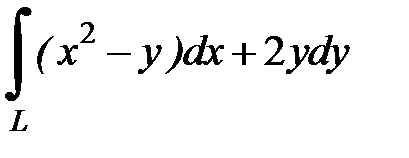 , где
, где  - дуга кубической параболы
- дуга кубической параболы 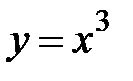 от точки
от точки 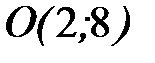 до точки
до точки 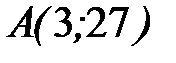 .
.
8.26. 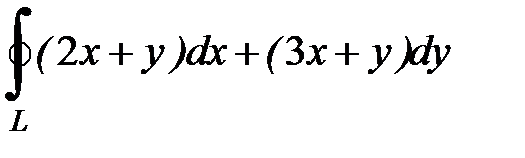 , где
, где  - окружность
- окружность 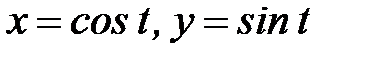 при положительном направлении обхода.
при положительном направлении обхода.
8.27. 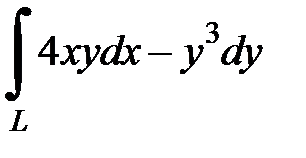 , где
, где 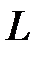 - ломаная
- ломаная 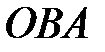 ;
; 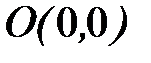 ;
; 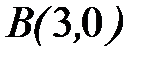 ;
; 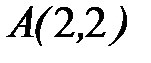 .
.
8.28. 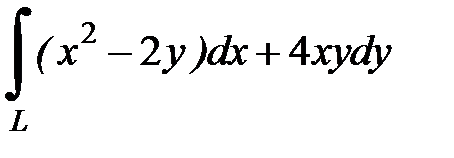 , где
, где 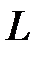 - отрезок прямой
- отрезок прямой 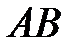 от точки
от точки 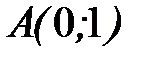 до точки
до точки 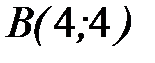 .
.
8.29. 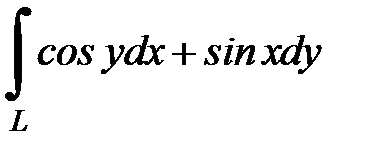 , где
, где 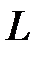 - отрезок прямой
- отрезок прямой 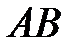 от точки
от точки 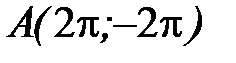 до точки
до точки 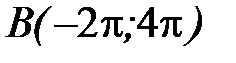 .
.
8.30. 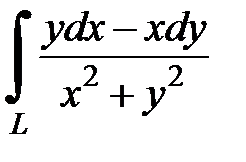 , где
, где 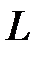 - отрезок прямой
- отрезок прямой 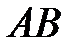 от точки
от точки 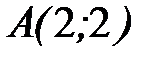 до точки
до точки 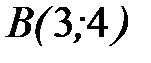 .
.
8.31. 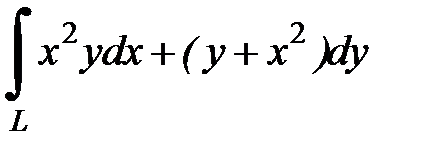 , где
, где  - дуга кубической параболы
- дуга кубической параболы 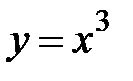 от точки
от точки 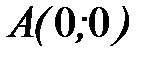 до точки
до точки 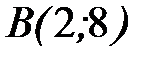 .
.
8.32. 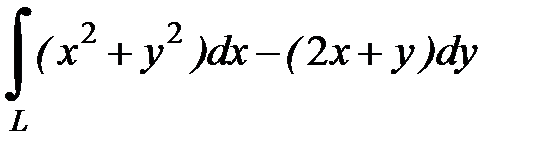 , где
, где 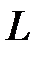 - ломаная
- ломаная 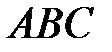 ;
; 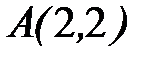 ;
; 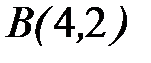 ;
; 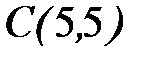 .
.
8.33. 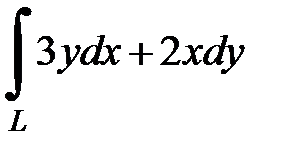 , где
, где  - дуга окружности
- дуга окружности 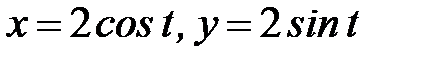 от точки
от точки 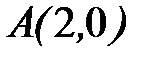 до точки
до точки 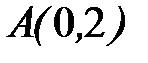 .
.
8.34. 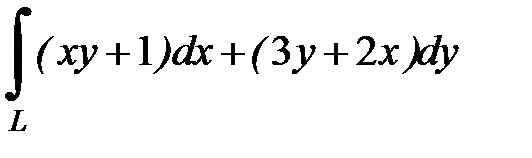 , где
, где  - дуга параболы
- дуга параболы 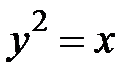 от точки
от точки 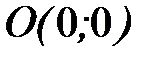 до точки
до точки 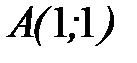 .
.
8.35. 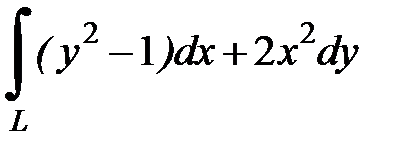 , где
, где  - дуга параболы
- дуга параболы 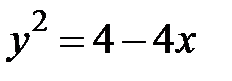 от точки
от точки 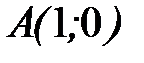 до точки
до точки 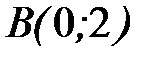 .
.
8.36. 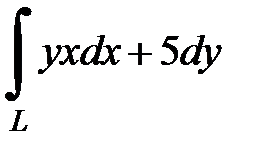 , где
, где  - дуга окружности
- дуга окружности 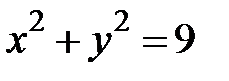 от точки
от точки 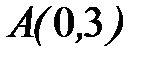 до точки
до точки 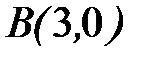 .
.
8.37. 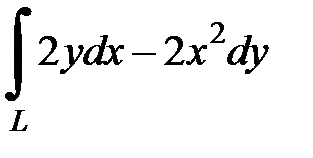 , где
, где  - дуга гиперболы
- дуга гиперболы  от точки
от точки 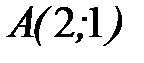 до точки
до точки 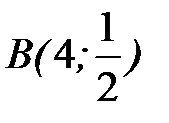 .
.
8.38. 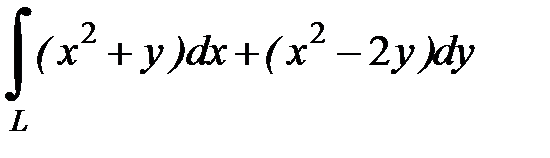 , где
, где 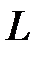 - ломаная линия
- ломаная линия 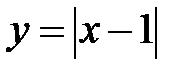 от точки
от точки 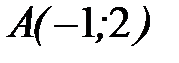 до точки
до точки 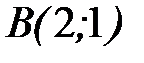 .
.
8.39. 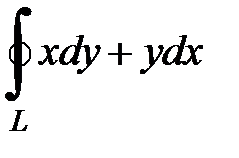 , где
, где  - контур треугольника с вершинами
- контур треугольника с вершинами 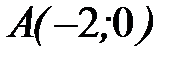 ,
, 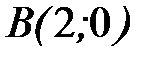 ,
, 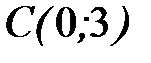 при положительном направлении обхода.
при положительном направлении обхода.
8.40. 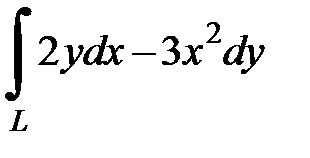 , где
, где  - дуга гиперболы
- дуга гиперболы 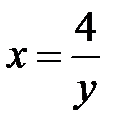 от точки
от точки 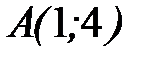 до точки
до точки 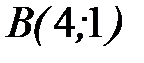 .
.
9. Вычислить тройной интеграл:
9.1. 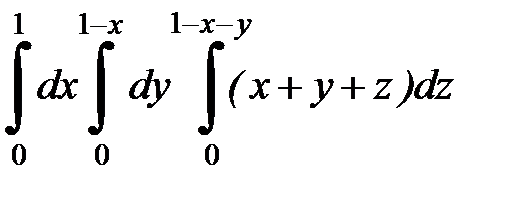
| 9.2. 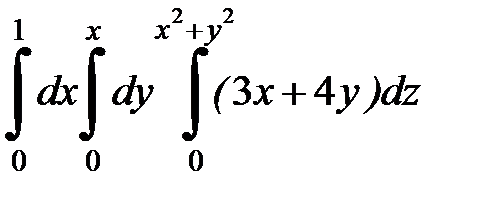
|
9.3. 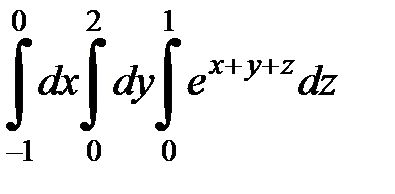
| 9.4. 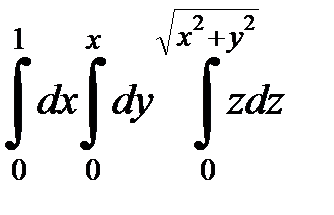
|
9.5. 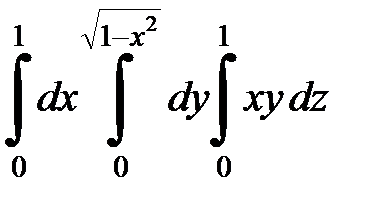
| 9.6. 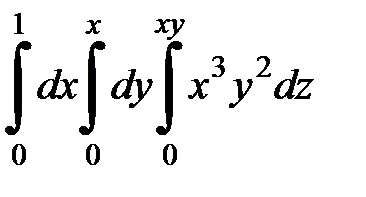
|
9.7. 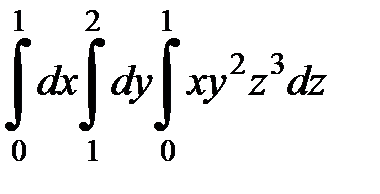
| 9.8. 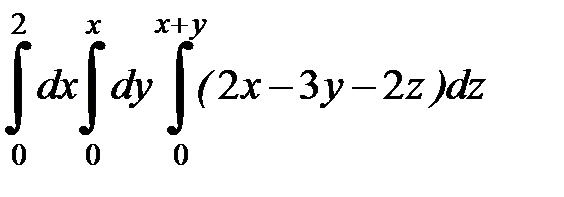
|
9.9. 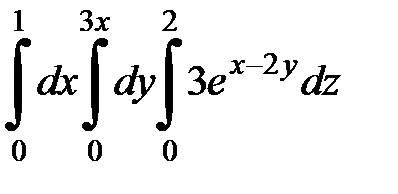
| 9.10. 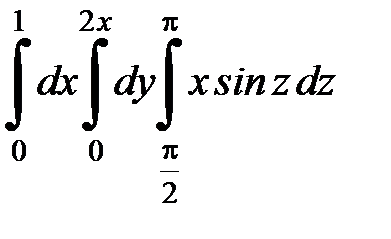
|
9.11. 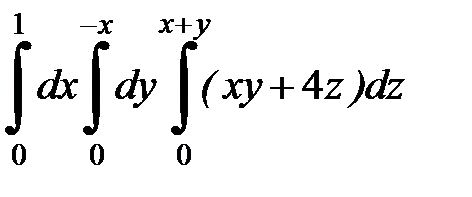
| 9.12. 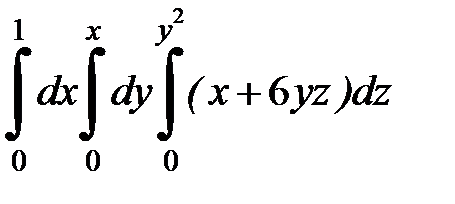
|
9.13. 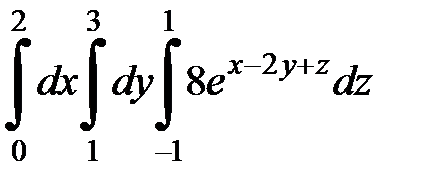
| 9.14. 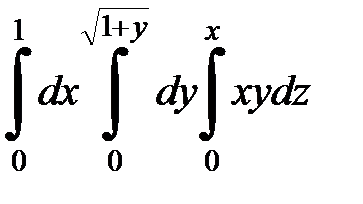
|
9.15. 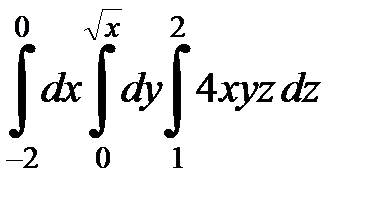
| 9.16. 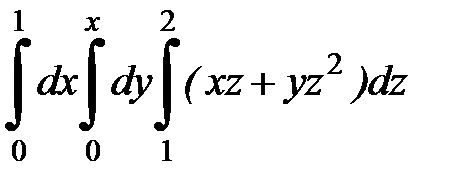
|
9.17. 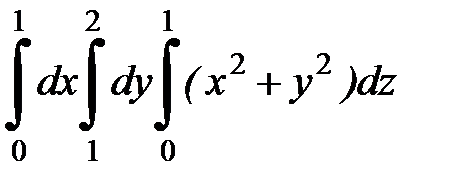
| 9.18. 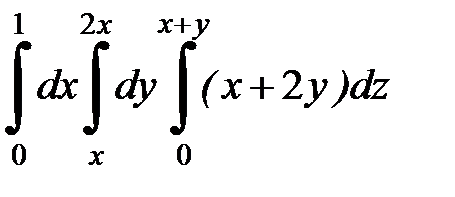
|
9.19. 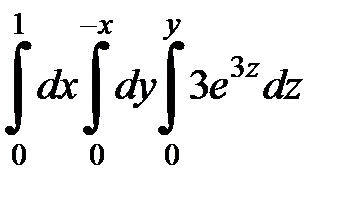
| 9.20. 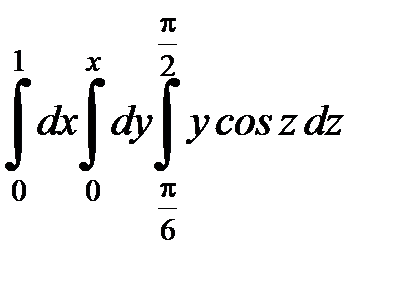
|
9.21. 
| 9.22. 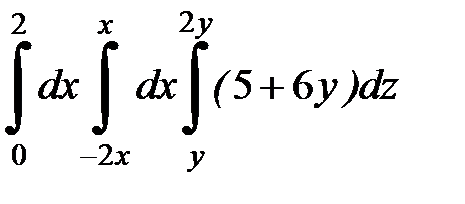
|
9.23. 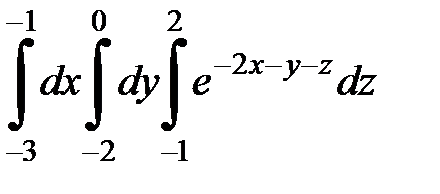
| 9.24. 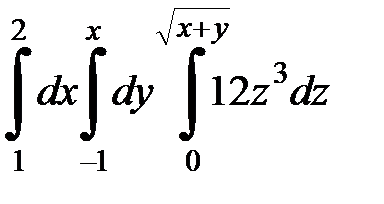
|
9.25. 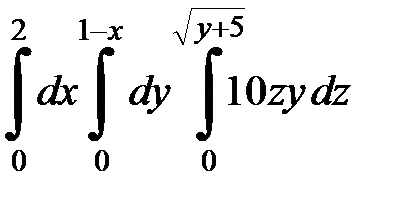
| 9.26. 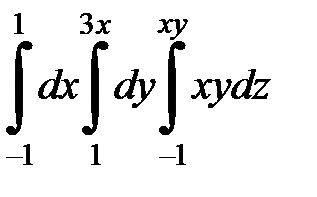
|
9.27. 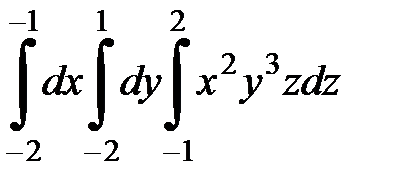
| 9.28. 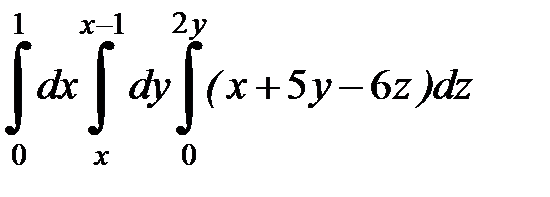
|
9.29. 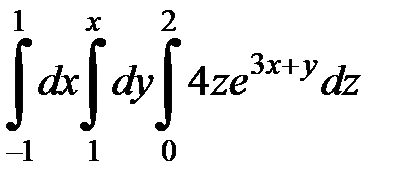
| 9.30. 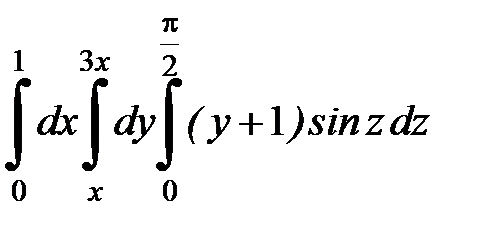
|
9.31. 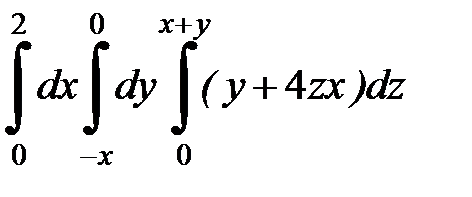
| 9.32. 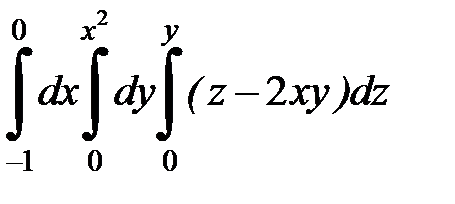
|
9.33. 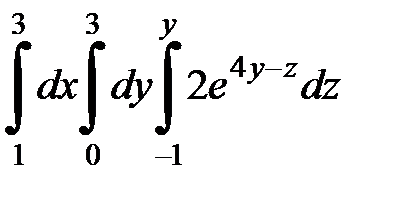
| 9.34. 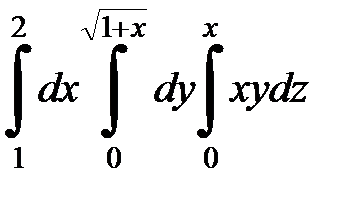
|
9.35. 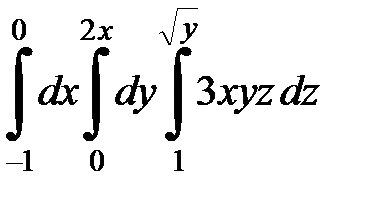
| 9.36. 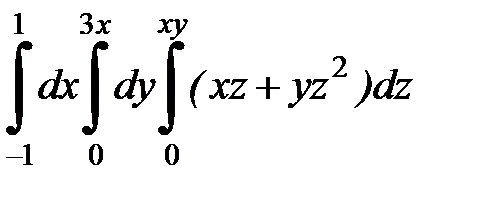
|
9.37. 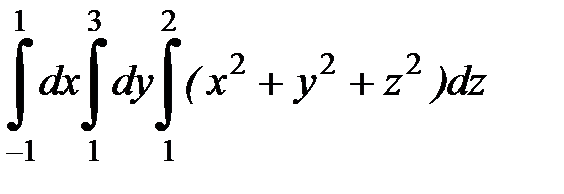
| 9.38. 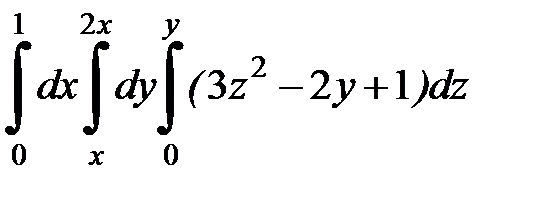
|
9.39. 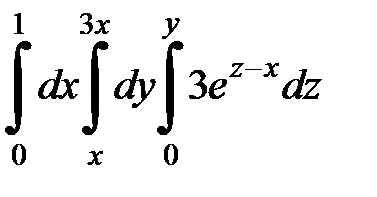
| 9.40. 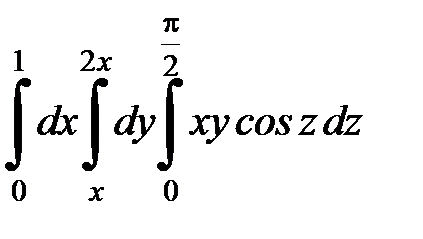
|
Дата добавления: 2022-06-11; просмотров: 27; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
