Определение рациональных способов раскроя материала.
Взадачах оптимального раскроя рассматриваются так называемые рациональные (оптимальные по Парето) способы раскроя. Предположим, что из единицы материала можно изготовить заготовки нескольких видов.
Способ раскроя единицы материала называется рациональным (оптимальным по Парето), если увеличение числа заготовок одного вида возможно только за счет сокращения числа заготовок другого вида.
Пусть к— индекс вида заготовки, к = 1,..., q;
i – индекс способа раскроя единицы материала, i= 1,..., q;
aik – количество (целое число) заготовок вида к, полученных при раскрое единицы материала i-м способом.
Приведенное определение рационального способа раскроя может быть формализовано следующим образом.
Способ раскроя v называется рациональным (оптимальным по Парето), если для любого другого способа раскроя iиз соотношений aik >avk , к=1, ..., q, следуют соотношения aik = avk , к=1, ..., q.
Определение интенсивности использования рациональных способов раскроя.
Обозначения:
j – индекс материала, j = 1,..., n;
к –индекс вида заготовки, к = 1, ..., q;
i – индекс способа раскроя единицы материала, i = 1,..., р;
ajik – количество (целое число) заготовок вида к, полученных при раскрое единицы j-го материала i-м способом;
bк – число заготовок вида к в комплекте, поставляемом заказчику;
dj – количество материала j-го вида;
xji – количество единичного материала, раскраиваемых по i-му способу (интенсивность использования способа раскроя);
|
|
|
cji — величина отхода, полученного при раскрое единицы j-го материала по i-му способу;
у — число комплектов заготовок различного вида, поставляемых заказчику.
Модель Араскроя с минимальным расходом материалов:
 (1)
(1)
 , где к = 1, ..., q (2)
, где к = 1, ..., q (2)
 , где j = 1,..., n; i = 1,..., р; (3)
, где j = 1,..., n; i = 1,..., р; (3)
Здесь (1) – целевая функция (минимум количества используемых материалов);
(2) – система ограничений, определяющих количество заготовок, необходимое для выполнения заказа;
(3) – условия неотрицательности переменных.
Специфическими для данной области приложения модели линейного программирования являются ограничения (2).
Модель В раскроя с минимальными отходами:
 (4)
(4)
 , где к = 1, ..., q (5)
, где к = 1, ..., q (5)
 , где j = 1,..., n; i = 1,..., р; (6)
, где j = 1,..., n; i = 1,..., р; (6)
Здесь (4) – целевая функция (минимум отходов при раскрое материалов);
(5) – система ограничений, определяющих количество заготовок, необходимое для выполнения заказа;
|
|
|
(6) – условия неотрицательности переменных.
Модель Сраскроя с учетом комплектации:
 , (7)
, (7)
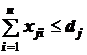 , где j = 1,..., n; (8)
, где j = 1,..., n; (8)
 , где к = 1, ..., q (9)
, где к = 1, ..., q (9)
 , где j = 1,..., n; i = 1,..., р; (10)
, где j = 1,..., n; i = 1,..., р; (10)
Здесь (7) – целевая функция (максимум комплектов, включающих заготовки различных видов);
(8) – ограничения по количеству материалов;
(9) – система ограничений, определяющих количество заготовок, необходимое для формирования комплектов;
(10) – условия неотрицательности переменных.
Специфическими для данной области приложения модели линейного программирования являются ограничения (9).
Дата добавления: 2018-02-15; просмотров: 97; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
