Методика выполнения в Microsoft Excel

1. Запустите программу Excel (Пуск ®Программы®Microsoft Excel) и создайте рабочую книгу Book.xls.

2. Создайте новый рабочий лист «Организация производства».

3. В ячейки E2, E3, иE4 занесите дневной запас микросхем – числа 500, 400, и 400 соответственно.

4. В ячейки B5, C5 и D5 занесите нули – в дальнейшем значения этих ячеек будут подобраны автоматически.

5. В ячейках диапазона A1:D4 разместите таблицу расхода комплектующих.

6. В ячейках F2:F4 нужно указать формулы для расчета расхода микросхем по типам. В ячейке F2 формула будет иметь вид =$B$5*B2+$C$5*C2+$D$5*D2, а остальные формулы можно получить методом автозаполнения (обратите внимание на использование абсолютных и относительных ссылок).

7. В ячейку F5 занесите формулу, вычисляющую общее количество произведенных приборов: для этого выделите диапазон B5:D5 и щелкните на кнопке Автосуммана стандартной панели инструментов.

8.Дайте команду Сервис®Поиск решения –откроется диалоговое окноПоиск решения.

9. В поле Установить целевуюукажите ячейку, содержащую оптимизируемое значение (F5). Установите переключатель Равной максимальному значению(требуется максимальный объем производства).

10. В поле Изменяя ячейкизадайте диапазон подбираемых параметров – B5:D5.

11. Необходимо добавить ограничения:

ü Расход микросхем не должен превышать их запас.

ü Количество выпускаемых приборов должно быть целым числом.

ü Число производимых приборов неотрицательно

12. Чтобы определить набор ограничений, щелкните на кнопке Добавить.В диалоговом окне Добавление ограниченияв поле Ссылка на ячейкуукажите диапазон F2:F4. В качестве условия задайте <=. В поле Ограничениезадайте диапазон E2:E4. Это условие указывает, что дневной расход комплектующих не должен превосходить запасов. Щелкните на кнопке ОК.

13. Снова щелкните на кнопке Добавить.В поле Ссылка на ячейкуукажите диапазон B5:D5. В качестве условия задайте >=. В поле Ограничениезадайте число 0. Это условие указывает, что число производимых приборов неотрицательно. Щелкните на кнопке ОК.

14. Снова щелкните на кнопке Добавить. В поле Ссылка на ячейку укажите диапазон B5:D5. В качестве условия выберите пункт цел. Это условие не позволяет производить доли приборов. Щелкните на кнопке ОК.

15. Щелкните на кнопке Выполнить.По завершении оптимизации откроется диалоговое окно Результаты поиска решения.

16. Установите переключатель Сохранить найденное решение,после чего щелкните на кнопке ОК.

17. Проанализируйте полученное решение. Кажется ли оно очевидным? Проверьте его оптимальность, экспериментируя со значениями ячеек B5:D5. Чтобы восстановить оптимальные значения, можно в любой момент повторить операцию поиска решения.

18. Сохранить рабочую книгу Book.xls.

Транспортная задача

Под термином "транспортные задачи" понимается широкий круг задач не только транспортного характера. Общим для них является, как правило, распределение ресурсов, находящихся у m производителей (поставщиков), по n потребителям этих ресурсов.

Ни автомобильном транспорте наиболее часто встречаются следующие задачи, относящиеся к транспортным:

· прикрепление потребителей ресурса к производителям;

· привязка пунктов отправления к пунктам назначения;

· взаимная привязка грузопотоков прямого и обратного направлений;

· отдельные задачи оптимальной загрузки промышленного оборудования;

· оптимальное распределение объемов выпуска промышленной продукции между заводами-изготовителями и др.

Рассмотрим экономико-математическую модель прикрепления пунктов отправления к пунктам назначения.

Имеются m пунктов отправления груза А₁, А₂, ..., А_m и объемы отправления по каждому пункту a₁, a₂, ..., a_m. Известна потребность в грузах b₁, b₂,...,b_n по каждому из n пунктов назначения B₁, B₂,..., B_n. Задана также матрица стоимостей с_ij, (i=1,2,...,m, j=1,2,...,n) доставки груза из пункта i в пункт j. Необходимо рассчитать оптимальный план перевозок, т. е. определить, сколько груза x_ij должно быть отправлено из каждого пункта отправления (от поставщика) в каждый пункт назначения (до потребителя) с минимальными суммарными транспортными издержками.

В общем виде исходные данные представлены в табл. 1.

Таблица 1. Исходные данные

Транспортная задача называется закрытой, если суммарный объем отправляемых грузов равен суммарному объему потребности в этих грузах по пунктам назначения

(1)

Если такого равенства нет (потребности выше запасов или наоборот), задачу называют открытой.

Для написания математической модели закрытой транспортной задачи необходимо все условия (ограничения) и целевую функцию представить в виде математических соотношений. Все грузы из i-х пунктов (поставщики) должны быть отправлены, т. е.:

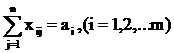
Все j-е пункты (потребители) должны быть обеспечены грузами в плановом объеме:

Из экономических соображений должно выполняться также условие неотрицательности переменных:

Перевозки необходимо осуществить с минимальными транспортными издержками. Следовательно, целевая функция примет вид:

(2)

Таким образом, математическая формализация простейшей транспортной задачи закрытого типа имеет следующий вид:

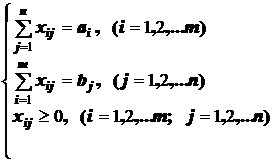В этой модели вместо матрицы стоимостей перевозок могут задаваться матрицы расстояний. В таком случае в качестве целевой функции рассматривается минимум суммарной транспортной работы. Как видно из выражения (1), уравнение баланса является обязательным условием решения закрытой транспортной задачи, поэтому, когда в исходных условиях дана открытая задача, то ее необходимо привести к закрытой форме. В случае если

· потребности по пунктам назначения превышают запасы пунктов отправления, то вводится фиктивный поставщик с недостающим объемом отправления;

· запасы поставщиков превышают потребности потребителей, то вводится фиктивный потребитель с необходимым объемом потребления.

Варианты, связывающие фиктивные пункты с реальными, имеют нулевые оценки. После введения фиктивных пунктов задача решается как закрытая.

Транспортным задачам присущи следующие особенности:

o распределению подлежат однородные ресурсы;

o условия задачи описываются только уравнениями;

o все переменные выражаются в одинаковых единицах измерения;

o во всех уравнениях коэффициенты при неизвестных равны единице;

o каждая неизвестная встречается только в двух уравнениях системы ограничений.

Транспортные задачи могут решаться симплексным методом. Однако перечисленные особенности позволяют для транспортных задач применять более простые распределительные методы решения.

На практике подобные задачи решаются, конечно же, при помощи различного программного обеспечения, что позволяет значительно упростить работу и сэкономить время.

Рассмотрим, как это можно сделать в среде электронных таблиц Microsoft Excel на примере следующей задачи

Дата добавления: 2018-02-15; просмотров: 103; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 Следующая ⇒

Мы поможем в написании ваших работ!