Формальная математическая постановки задачи. Министерство образования Российской Федерации

Стр 1 из 6Следующая ⇒

Министерство образования Российской Федерации

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

"УДМУРТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ"

Институт экономики и управления

КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ И ИНФОРМАТИКИ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по выполнению лабораторной работы

"Решение задач оптимизации

в среде Microsoft Excel"

для студентов дневного и заочного отделений

Составители:

Москалева Л.А., ст. преподаватель

Кассихина Ф.Н., вед. инженер

Сметанин Ю.М., к.ф.-м.н., доцент

Ижевск

2007

СОЖЕРЖАНИЕ

	Стр.
Введение
Формальная постановка задачи оптимизации планирования производства
Пример формальной постановки задачи оптимизации планирования производства
Методика выполнения задачи оптимизации планирования производства в Microsoft Excel
Формальная постановка задачи оптимизации транспортных перевозок
Пример формальной постановки транспортной задачи
Методика выполнения транспортной задачи в Microsoft Excel
Требования к оформлению лабораторной работы
Рекомендуемая литература

Введение

В повседневной жизни мы часто сталкиваемся с необходимостью решать оптимизационные задачи. Например, заходя в магазин, мы стоим перед дилеммой максимального удовлетворения своих потребностей, соизмеряя их с возможностями нашего кошелька.

Любой менеджер постоянно решает разнообразные проблемы, начиная с планирования штата сотрудников, фонда зарплаты и заканчивая составлением оптимального плана производства, планированием рекламной кампании по продвижению продукции и оптимизацией капиталовложений.

На театре военных действий командиры решают задачи оптимального указания целей и наведения оружия на эти цели в расчете на максимальное поражение противника.

Менеджер по транспортным перевозкам решает задачу минимизации транспортных издержек в условиях наиболее полного удовлетворения интересов производителей и потребителей.

Настоящее методическое пособие посвящено знакомству с задачами оптимизации, решаемых на предприятиях и одной из самых популярных экономико-математических моделей - транспортной задаче.

Студент экономических специальностей должен знать основные экономические проблемы, при решении которых возникает необходимость в математическом инструментарии. Он должен ориентироваться в экономической постановке задачи, уметь формализовать экономическую задачу, то есть описать ее с помощью известной математической модели, провести расчеты и получить количественные результаты. Однако самое главное – студент должен уметь анализировать эти результаты и делать выводы, адекватные поставленной экономической задаче.

В результате изучения методического пособия студент должен научиться определять и использовать для экономического анализа:

• целевую функцию;

• ограничения;

• модель линейного программирования;

• оптимальный план.

Для решения задач оптимизации часто используют надстройку программы Microsoft Excel "Поиск решения".

Цель методического пособия – научиться использовать возможности Microsoft Excel для нахождения решений задач оптимизации.

Оптимизация плана производства

Общая постановка задачи планирования производства: необходимо определить план производства одного или нескольких видов продукции, который обеспечивает наиболее рациональное использование имеющихся материальных, финансовых и других видов ресурсов. Такой план должен быть оптимальным с точки зрения выбранного критерия — максимума прибыли, минимума затрат на производство и т.д.

Модели

Введем обозначения:

п — количество выпускаемых продуктов;

т — количество используемых производственных ресурсов (например, производственные мощности, сырье, рабочая сила);

a_ij — объем затрат i-го ресурса на выпуск единицы j-й продукции;

c_j— прибыль от выпуска и реализации единицы j-го продукта;

b_i— количество имеющегося i-го ресурса;

x_j— объем выпуска j-го продукта.

Формально задача оптимизации производственной программы может быть описана с помощью следующей модели линейного программирования:

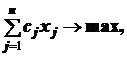(1)

(2)

(3)

Здесь (1) — целевая функция (максимум прибыли);

(2) — система специальных ограничений (constraint) на объем фактически имеющихся ресурсов;

(3) — система общих ограничений (на неотрицательность переменных);

x_j— переменная (variable).

Задача (1)—(3) называется задачей линейного программирования в стандартной форме на максимум.

Задача линейного программирования в стандартной форме на минимумимеет вид

(4)

(5)

(6)

Вектор х = (x₁, x₂, ..., x_п), компоненты x_j которого удовлетворяют ограничениям (2) и (3) (или (5) и (6) в задаче на минимум), называется допустимым решением или допустимым планом задачи линейного программирования (ЛП).

Совокупность всех допустимых планов называется множеством допустимых планов.

Допустимое решение задачи ЛП, на котором целевая функция (1) (или (3) в задаче на минимум) достигает максимального (минимального) значения, называется оптимальным решением задачи ЛП.

С каждой задачей ЛП связывают другую задачу ЛП, которая записывается по определенным правилам и называется двойственной задачей ЛП.

Двойственной к задаче ЛП (1)–(3) является задача

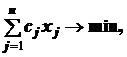(7)

(8)

(9)

Соответственно, двойственной к задаче ЛП (7)–(9) является задача (1)–(3). Каждой переменной (специальному ограничению) исходной задачи соответствует специальное ограничение (переменная) двойственной задачи. Если исходная задача ЛП имеет решение, то имеет решение и двойственная к ней задача, при этом значения целевых функций для соответствующих оптимальных решений равны.

Компонента 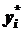оптимального решения двойственной задачи (7)–(9) называется двойственной оценкой (Dual Value)ограничения исходной задачи ЛП.

Пусть 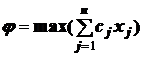, где х_j – компонента допустимого решения задачи (1)–(3).

Тогда при выполнении условий невырожденности оптимального решения имеют место следующие соотношения:

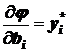, i=1, …, m

Изменим значение правой части b_iодного основного ограничения (RHS) исходной задачи ЛП.

Пусть 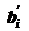– минимальное значение правой части основного ограничения, при котором решение у^*двойственной задачи не изменится. Тогда величину 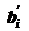называют нижней границей (Lower Bound) устойчивости по правой части ограничения.

Пусть –максимальное значение правой части основного ограничения, при котором решение у^*двойственной задачи не изменится. Тогда величину называют верхней границей (Upper Bound) устойчивости по правой части ограничения.

Изменим значение одного коэффициента с_j целевой функции исходной задачи ЛП.

Пусть Су'— минимальное значение коэффициента целевой функции, при котором оптимальное решение х исходной задачи не изменится. Тогда величину Cj называют нижней границей устойчивости по коэффициенту целевой функции.

Пусть с" — максимальное значение коэффициента целевой функции, при котором оптимальное решение х* исходной задачи не изменится. Тогда величину cj называют верхней границей устойчивости по коэффициенту целевой функции.

Пример решения задачи

Оптимизации планирования производства

Задача.Завод производит электронные приборы трех видов (прибор А, прибор В и прибор С), используя при сборке микросхемы трех видов (тип 1, тип2, тип3). Расход микросхем задается следующей таблицей:

	Прибор А	Прибор В	Прибор С
Микросхема 1	2	5	1
Микросхема 2	2	0	4
Микросхема 3	2	1	1

Стоимость изготовленных приборов одинакова. Ежедневно на склад завода поступает 500 микросхем типа 1 и по 400 микросхем типов 2 и 3. Каково оптимальное соотношение дневного производства приборов различного типа, если производственные мощности завода позволяют использовать запас поступивших микросхем полностью?

Формальная математическая постановки задачи

Константы

1. Пусть m_ij – расход микросхем i для прибора j, где i=1,2,3; j=1,2,3.

	2	5	1
m_ij=	2	0	4
	2	1	1

2. Пусть Z_i – ежедневный запас микросхем i на складе, где i=1,2,3.
Z₁=500; Z₂=400; Z₃=400.

Переменные

1. Обозначим через x_j дневное производство приборов j, j=1,2,3, то есть
x₁ - дневной выпуск приборов А;
x₂ - дневной выпуск приборов В;
x₃ - дневной выпуск приборов С.

2. Обозначим через R_i расход микросхем i, где i=1,2,3, то есть
R₁ - расход микросхем 1-го типа;
R₂ – расход микросхем 2-го типа;
R₃ – расход микросхем 3-го типа.

3.Обозначим через N дневное производство всех видов приборов.

Решение

1.Зададим математическую модель расхода микросхем

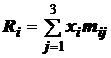
, где i=1,2,3.

или

2. Зададим математическую модель нахождения общего количества приборов N=x₁+x₂+x₃. Его максимизация является целью решения задачи. Следовательно, целевая функция будет иметь вид:

Ограничения

1. Расход микросхем не должен превышать их запас

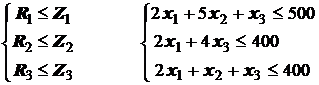(для микросхем 1-го типа)

или (для микросхем 2-го типа)

(для микросхем 3-го типа)

2. Количество выпускаемых приборов должно быть целым числом.

3. Поскольку x₁, x₂, x₃ выражают объем выпускаемых приборов, то они не могут быть отрицательны, то есть
x₁≥0; x₂≥0; x₃≥0; x₄≥0

Дата добавления: 2018-02-15; просмотров: 294; Мы поможем в написании вашей работы!
Поделиться с друзьями:

12 3 4 5 6 Следующая ⇒

Мы поможем в написании ваших работ!