Общие случаи пересечения плоскостей
86*. Найти линию пересечения плоскостей,_заданных треуголь-
ником ABC и параллельными прямыми ED и FG (рис. 84,а).
.
Решение. В данном случае общие точки для обеих плоскостей можно найти
как точки пересечения (М и N) сторон треугольника АВ и АС с плоскостью, заданной прямыми ED и FG (рис. 84, б).
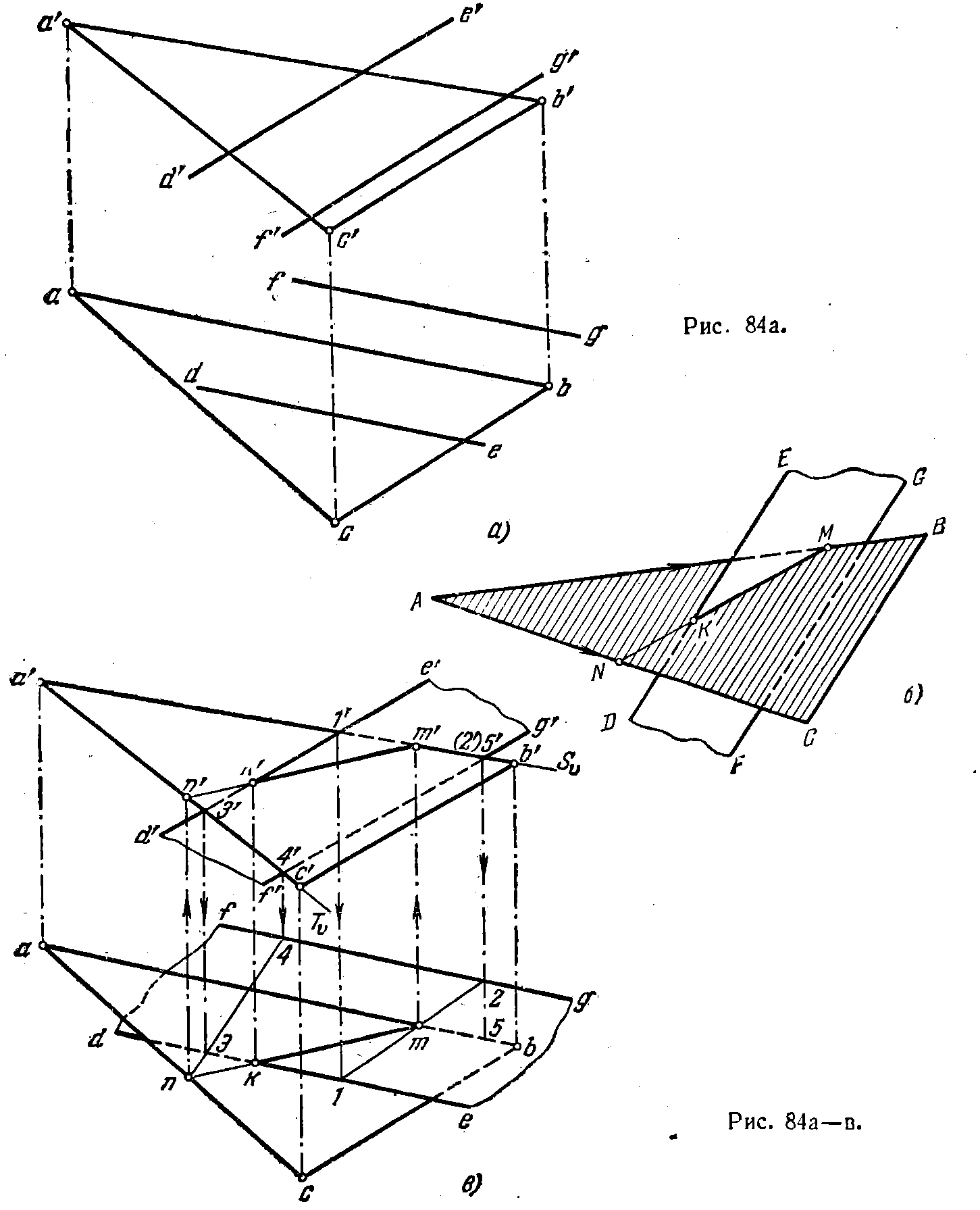
Рис.84 а-б
. 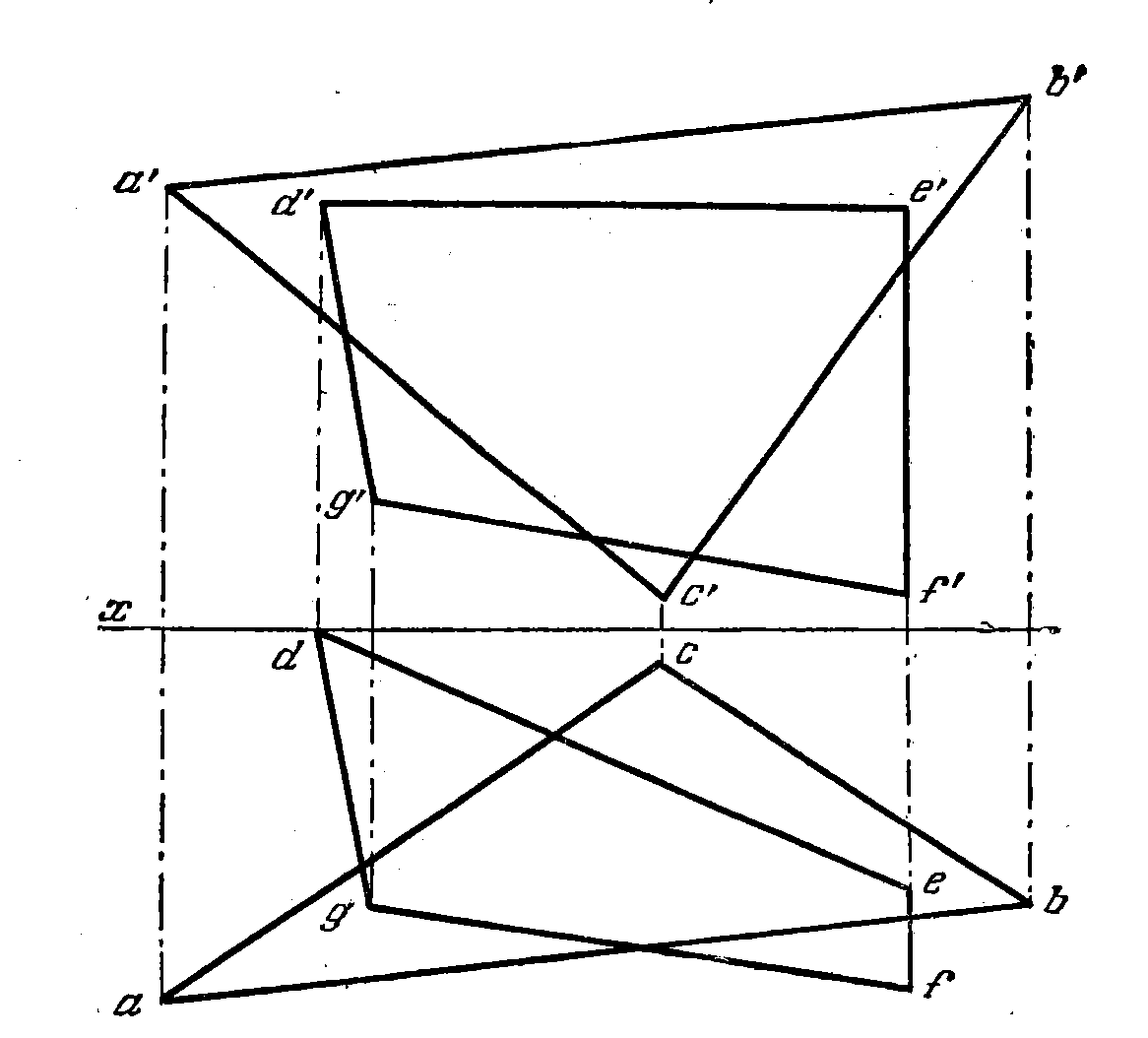
Рис.85
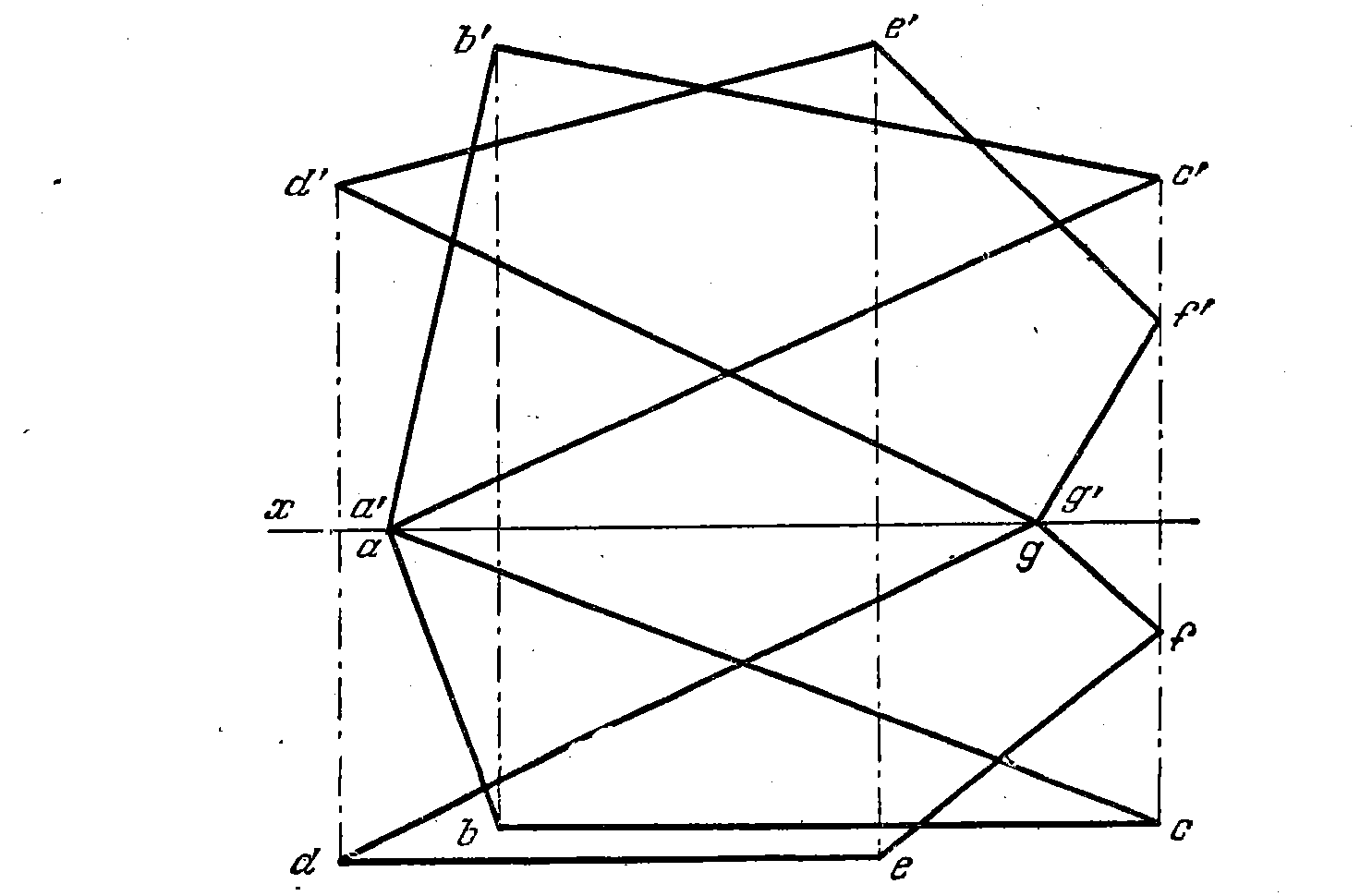
Рис. 86
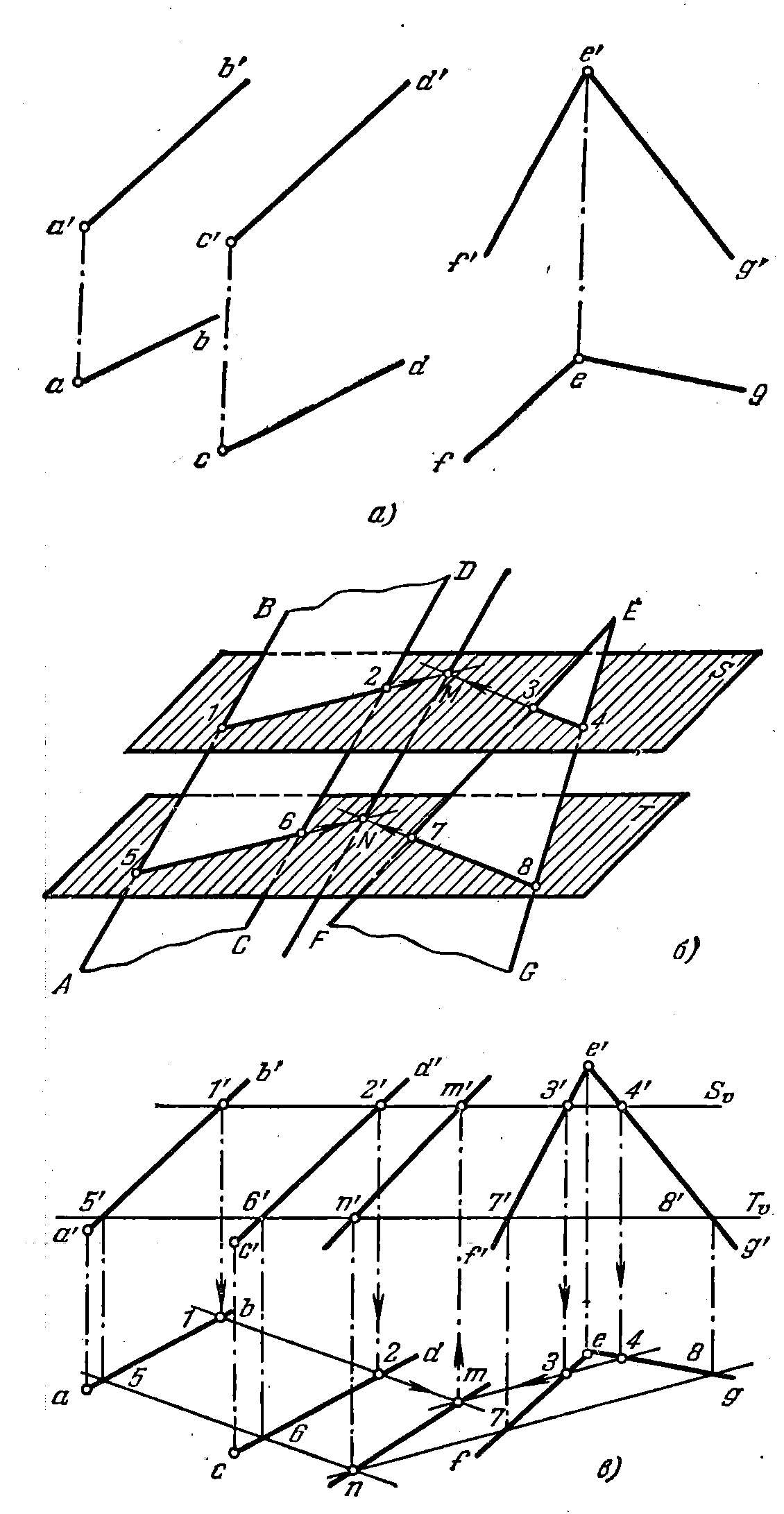
Рис.87
d' 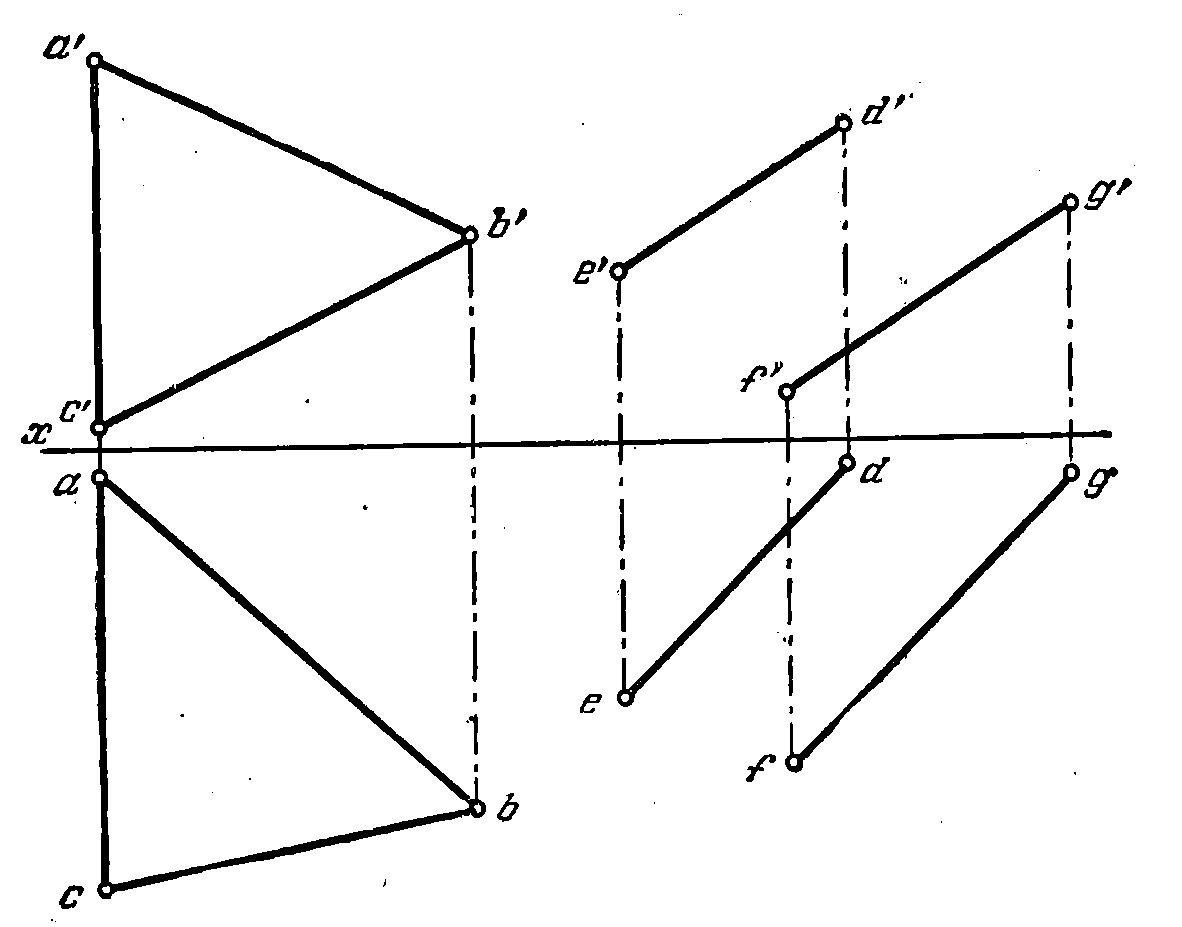
Рис. 88.

Рис. 89.
Через прямую А В проводим фронтально-проецирующую плоскость S, задав ее следом Sv (рис. 84, в). Она пересекает плоскость параллельных прямых по прямой 1—2(1'2', 1—2), которая пересекается со стороной АВ в точке М (mm').Фронтально-проецирующая плоскость Т, проведенная через прямую АС, задана следом Tv; эта плоскость пересекает плоскость параллельных прямых по линии 3—4( 3'4', 3—4), которая в пересечении со стороной АС дает точку N (п, п'). Искомая линия пересечения плоскостей проходит через точки М и N.
Для определения видимости плоскостей при взаимном их пересечении следует вообще применять прием, указанный, например, при решении задачи 77. Рассмотрим точки 2 (лежит на прямой FG) и 5 (лежит на прямой АВ). Анализ положения этих точек показывает, что на пл. V точка ,5 закрывает точку 2, а это значит, что прямая АВ в этом месте проходит перед FG, т. е. треугольник ABC виден до прямой КМ. Остальное ясно из чертежа.
|
|
|
87. Найти линию пересечения плоскостей, заданных треуголь-
ником ABC и четырехугольником DEFG (рис. 85).
88. Найти линию пересечения плоскостей, заданных треугольни-
ком ЛВС и четырехугольником DEFG (рис. 86).
_ 89*. Найти линию пересечения плоскостей, из которых одна
задана параллельными прямыми АВ и CD, а другая — пересекающи-
мися FE и EG (рис. 87, а).
Решение. Для нахождения общих точек данных плоскостей введены две вспомогательные плоскости S и Т (рис. 87, б) и построены линии пересечения этих плоскостей с заданными. Через точки М и N пересечения этих линий проходит искомая прямая. На рис. 87, в плоскости S и Т параллельны пл. Н. Они пересекают заданные плоскости по горизонталям 1—2, 3—4 и 5—6, 7—8 (см. задачу 67).
Прямые 1 — 2 и 3—4, пересекаясь, дают точку М (m, m'), а прямые 5—6
и 7 — 8 — точку N (n, n'). Прямая MN (mn, m'n') — искомая линия пересече-
ния плоскостей.
90. Найти линию пересечения плоскостей, из которых одна за-
дана треугольником ABC, а другая — параллельными прямыми ED
и FG (рис. 88).
91. Найти линию пересечения плоскостей, из которых одна
|
|
|
задана треугольником DEF. другая — прямой ВС и точкой А.(Рис 89)
ВОПРОСЫ.
Как задается плоскость на чертеже?
Что такое след плоскости на плоскости проекций?
Где располагаются фронтальная проекция горизонтального следа и горизонтальная проекция фронтального следа плоскости?
Как определяется на чертеже, принадлежит ли прямая данной плоскости?
Дата добавления: 2018-02-18; просмотров: 626; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
