Пересечение прямой с плоскостью общего положения
77*. Найти точку пересечения прямой А В с плоскостью, задан-
ной треугольником CDE (рис. 75, а). 
Рис.75 а,б.
Решение. Как известно, для нахождения точки пересечения прямой с пло-
скостью общего положения следует через прямую провести вспомогательную плоскость (R), построить линию пересечения этой плоскости с заданной (/—2) и найти точку пересечения (К) заданной и построенной прямых. Точка К является искомой точкой пересечения прямой с плоскостью (рис. 75, б). В качестве вспомогательной плоскости
обычно используют горизонтально- или фронтально-проецирующую
плоскость.

Рис.75 в,г.
На рис. 75, в через прямую А В проведена фронтально-проецирующая плоскость R, ее след Rv совпадает с а'в'. Горизонт, след плоскости в данной задаче не нужен и поэтому не показан.
Строим линию пересечения плоскости R и плоскости, заданной треугольником CDE (пример такого построения см. в задаче 67). Построив линию 1—2 (рис. 75, в), находим точку пересечения ее с прямой АВ — точку К (k, k').
Для определения участков прямой АВ, которые будут закрыты треугольником, следует воспользоваться анализом положения точек на скрещивающихся прямых.
Например, точки / и 3 находятся на скрещивающихся прямых (соответственно) ED и АВ. Фронтальные проекции этих точек совпадают, т. е. точки / и 3 одинаково удалены от пл. Н. Но расстояния их от пл. V различны: точка 3 находится дальше от пл. V, чем точка /. Поэтому по отношению к пл. V точка 3 закрывает точку / (направление взгляда указано стрелкой i). Следовательно, прямая АВ проходит перед треугольником CDE до точки К. Начиная же от точки К влево прямая АВ
|
|
|
Рис. 76, 77
закрывается треугольником, и поэтому этот участок прямой показан штриховой линией.
Для выявления невидимого участка на горизонт, проекции прямой А В рассмотрим точки 4 и 5, лежащие соответственно на прямых АВ и CD.
Если смотреть на эти точки по направлению s1 мы видим сначала точку S. Точка 4 закрывается точкой 5. Следовательно, прямая АВ в этом месте закрыта треугольником CDE, и участок ее проекции от точки k до точки 4 должен быть показан штриховой линией. В данном случае точка К оказалась внутри контура треугольника CDE.
При ином взаимном положении пересекающихся элементов возможен случай, когда точка К окажется вне треугольника (рис. 75, г). Это означает, что прямая АВ пересекает плоскость, заданную треугольником CDE, вне контура этого треугольника. АВ становится невидимой за точкой К (влево)
.
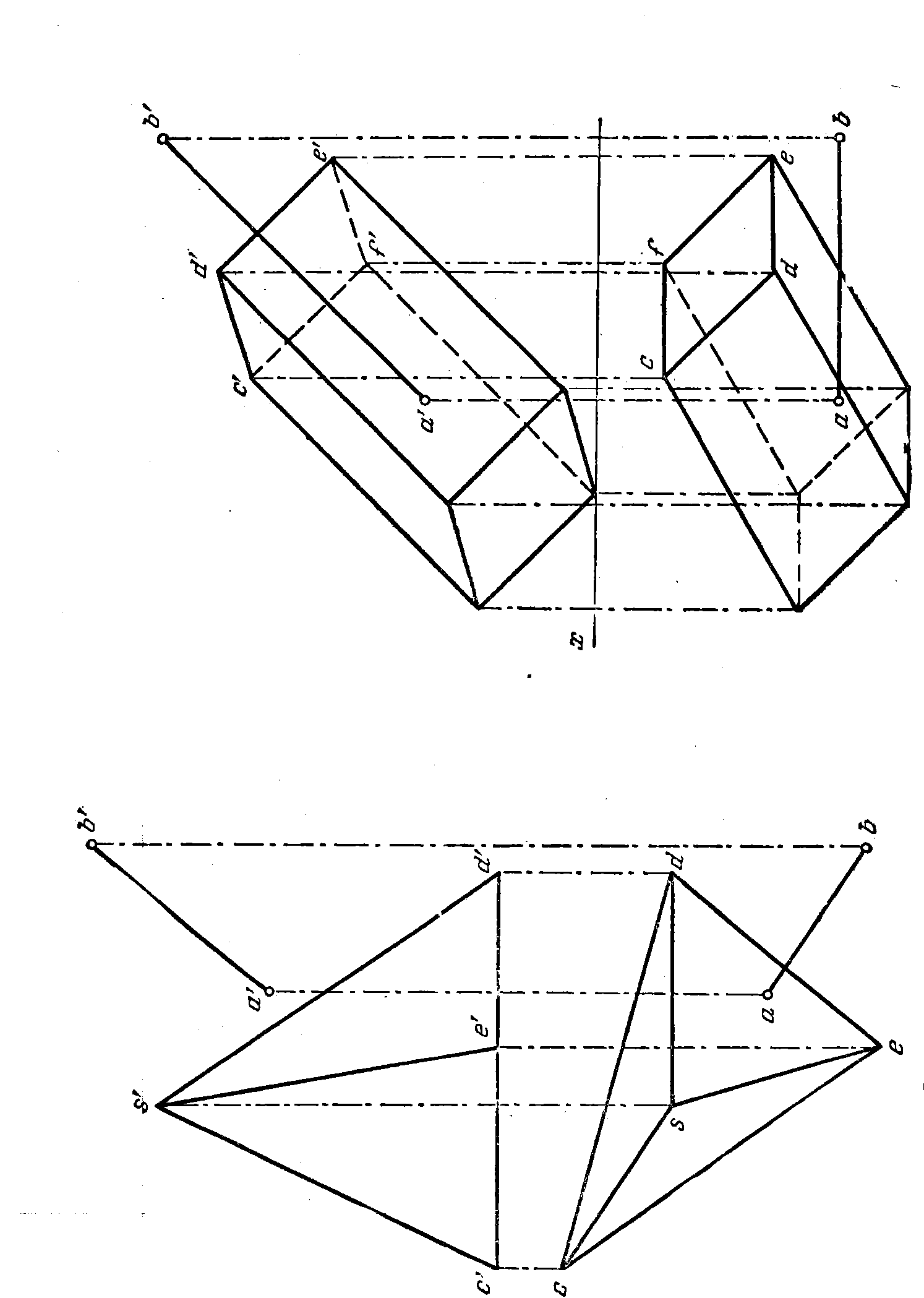
78. Найти точки пересечения прямой АВ с гранями пирамиды (рис. 76). Грани пирамиды следует рассматривать как плоскости,заданные треугольниками.
|
|
|
79. Найти точки пересечения прямой АВ с гранями призмы
(рис. 77). Грани призмы следует рассматривать как плоскости, задан-
ные параллельными прямыми.
80*. Найти точки пересечения прямой АВ с плоскостью Р (рис. 78, а). 
Рис.78 а,б.
Решение. Проводим через прямую АВ (рис 78,б и в) фронтально-проецирую-
щую плоскость R (ее след Rv совпадает с а'Ь') и строим линию MN пересечения обеих плоскостей — заданной и проведенной через АВ (построение подобно выполненному в задаче 70). Искомая точка K{k, к') пересечения прямой АВ с плоскостью Р находится в точке пересечения MN с АВ.
В данной задаче видимость участка прямой от точки А до К очевидна; однако
в более сложных случаях следует видимый участок прямой определять на основании
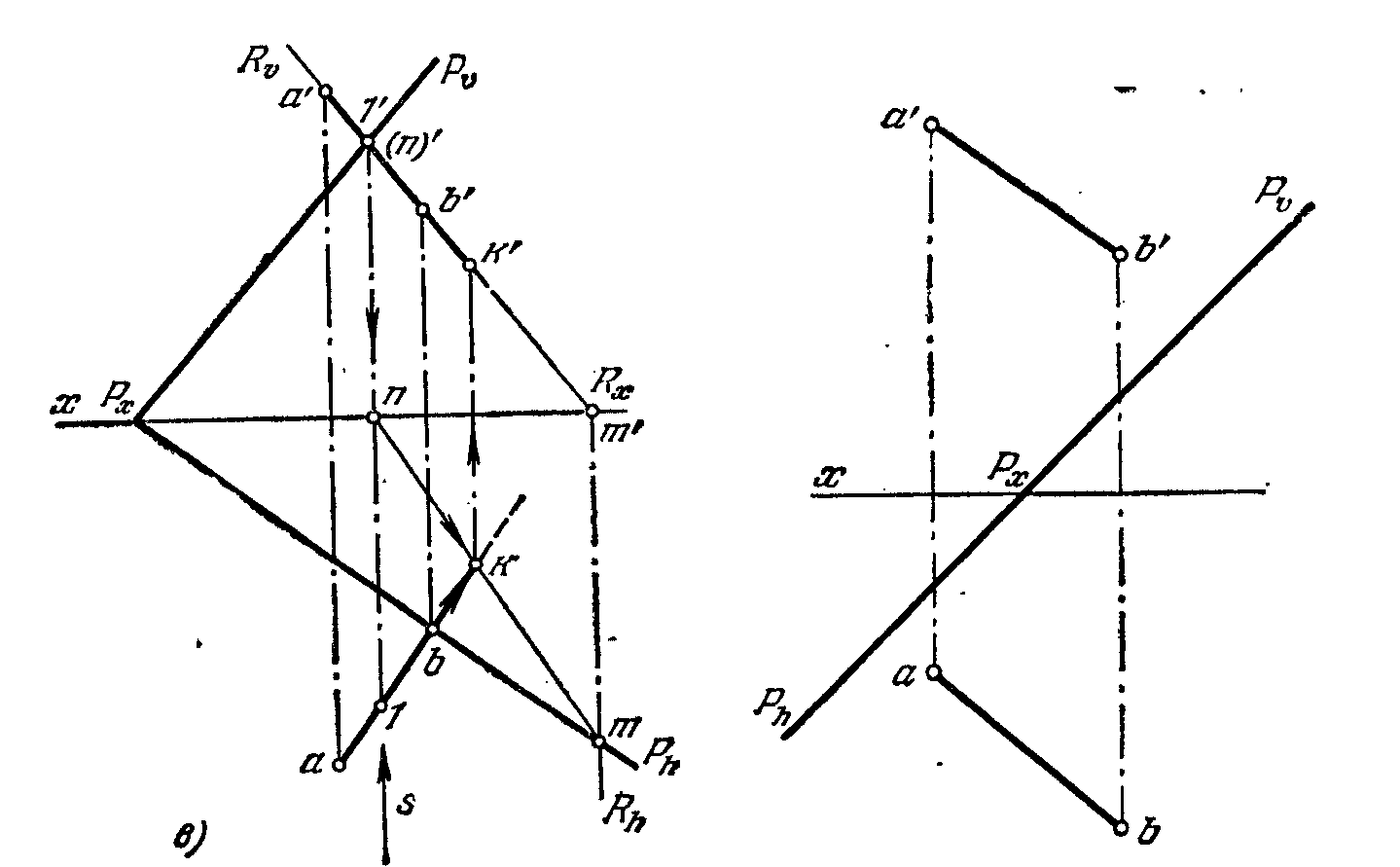
Рис.78 в Рис.79
анализа положения точек. Например, взяв точку / (на прямой АВ) и точку N (на следе Рv), видим, что точка / располагается дальше относительно пл. V, чем точка N. Следовательно, прямая АВ до точки К видима. За точкой К прямая показана штриховой линией — она невидима. Аналогично определяется видимость на горизонт, проекции.
|
|
|
81. Найти точку пересечения прямой АВ с плоскостью Р (рис. 79).
82*. Найти точку пересечения прямой АВ с плоскостью Р (рис. 80, а).
Решение. Через прямую А В проводим горизонтально-проецирующую пло-
скость R (след R/, совпадает с ab) и строим линию пересечения плоскостей Р и R. используя точки М и N пересечения их одноименных следов (рис. 80, б и в). Искомая точка (k', k) находится в точке пересечения М N с А В. На рис, 80, г точка К построена с помощью пл. W. Так как пл. Р профильно-проецирующая (рис. 80, б),

Рис.80 а-г
то профильная проекция k" лежит в точке пересечения следа Pw с а"Ь". Зная k",строим К' на а'Ь' и k на ab. Видимые участки прямой АВ определяются так же, как в задачах 77 и 80.
83. Найти точку пересечения прямой АВ с плоскостью Р (рис. 81).
84*. Найти точку пересечения прямой А В с плоскостью, заданной
треугольником CDE (рис. 82, а).
Решение. Через прямую АВ проводим (рис. 82, б и в) пл. R, параллельную
пл. W. Она пересекает заданную плоскость по прямой MN (точки m', n', m и n лежат на пересечении следов Rv и Rh с одноименными проекциями соответствующих сторон

Рис. 81.
|
|
|

Рис. 82а. б. 
Рис.82 в
треугольника CDE). Так как прямые АВ и MN профильные, то для нахождения точки (К) их пересечения строим профильные проекции а"Ь" и m"n". Проекция k" находится на пересечении а"Ь" и m"n". По k" строим к' на а'Ь' и k на ab.

Рис. 83.
85. Найти точку пересечения прямой EF с плоскостью, заданной
четырехугольником A BCD (рис. 83).
Дата добавления: 2018-02-18; просмотров: 1252; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
