И ДВУХ ПЛОСКОСТЕЙ МЕЖДУ СОБОЙ
Пересечение прямой с проецирующей плоскостью
61*. Найти точку пересечения прямой А В с пл. Т (рис. 59, а),
заданной ее фронт, следом Tv.
Решение. В данном случае пл. Т параллельна пл. Н и, следовательно, перпендикулярна к фронт, плоскости проекций; для пл. Т в системе V, Н
дан только фронт.

Рис. 59 а,б,в.
след Tv, параллельный оси проекций х. Очевидно, фронт, проекция (k') искомой точки пересечения должна лежать как на следе Tv, так и на фронт, проекции прямой АВ, т. е. на а'Ь' (рис. 59, б). Поэтому точку k' (рис. 59, в) находим в точке пересечения следа Tv с проекцией а'Ь'. По точке k' находим точку k на ab.
Так как прямая АВ в направлении от К к А находится под пл. Т, то на чертеже
соответствующая часть горизонт, проекции изображена штриховой линией.
62. Найти точку пересечения прямой А В с пл. S (рис. 60).
63*. Найти точку пересечения прямой АВ с пл. R (рис. 61, а).

Рис. 60.
Решение. Пл. R является фронтально-проецирующей. Очевидно, фронт,
проекция (k') искомой точки пересечения должна находиться как на следе Rv, так и на фронт, проекции прямой АВ, т. е. на а'Ь' (рис. 61, б).
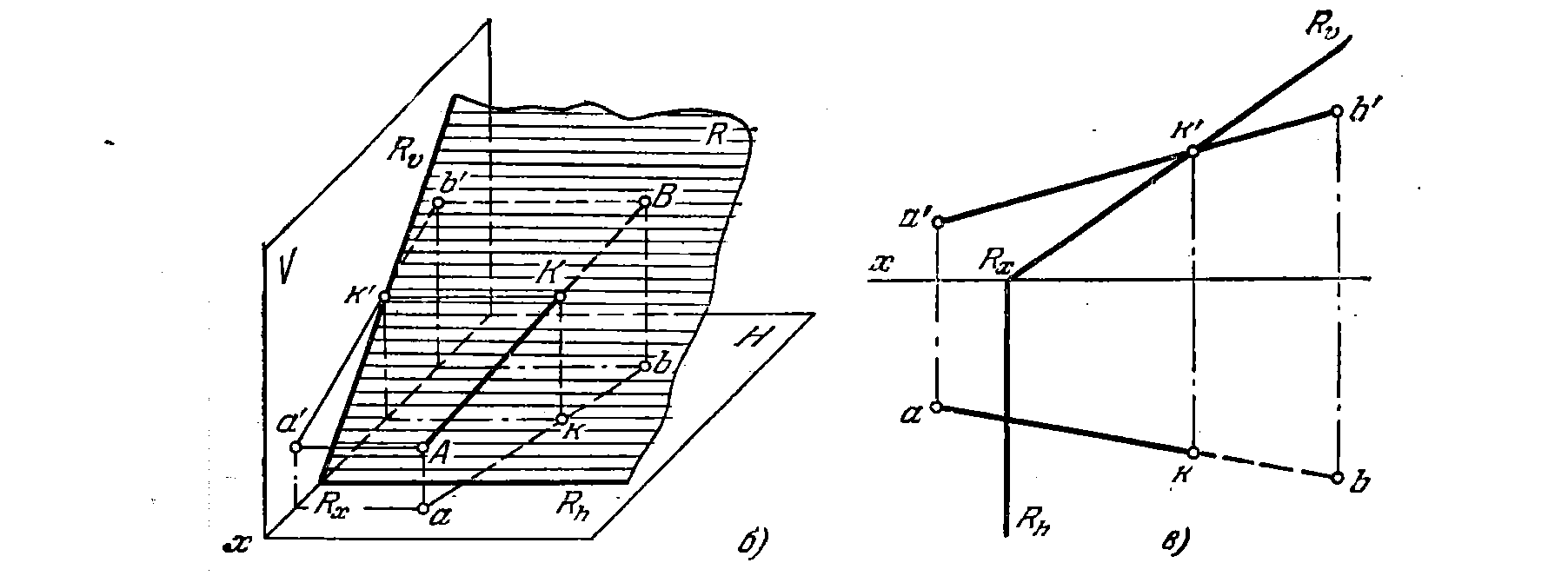
Рис 61 а,б,в.
На чертеже .(рис. 61, в) находим к' в точке пересечения следа Rv с а'Ь',
а проекцию k — на a b. Прямая А В в направлении от К к В находится под пл. R; поэтому на чертеже соответствующая часть горизонт, проекции изображена штриховой линией.
|
|
|
84*. Найти точку пересечения прямой АВ о ил. R (риc. 62, а).
Решение. Пл. R является горизонтально - прецирующей.

Рис.62 .а,б.

Рис.62 в Рис.63 а Очевидно, горизонт,проекция искомой точки пересечения должна находиться как на следе Rh так и на аЬ (рис. 62, б). Поэтому точку k (рис. 62, в) получаем как точку пересечения следа Rh
с аb. По точке к находим проекцию k' на а'Ь'.
Прямая АВ в направлении от К к В находится за плоскостью R; на чертеже соответствующая часть фронт, проекции изображена штриховой линией.
65*. Найти точку пересечения прямой АВ а плоскостью, заданной
треугольником CDE (рис. 63, а).
Решен и.е. Замечаем, что плоскость треугольника перпендикулярна к пл. Н.
Проекция k точки пересечения должна лежать как на прямой cd тaк. и на аb

Рис63 б, в.
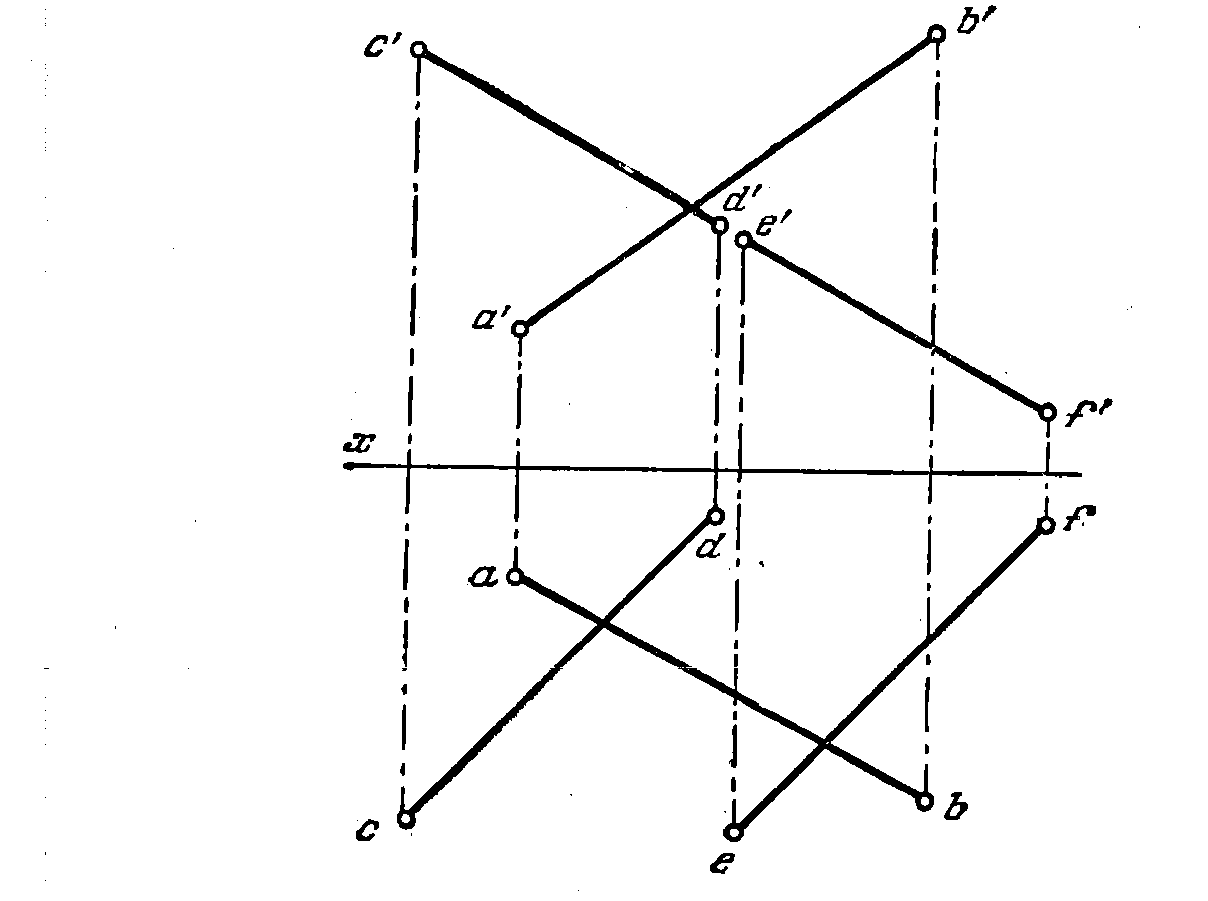
Рис. 64
(рис. 63, б и в). По точке k находим к' на а'Ь',
Так как прямая АВ в направлении от К к А находится за треугольником CDE
|
|
|
(рис. 63, в), то на чертеже соответствующая часть фронт, проекции прямой изображена штриховой линией.
66. Найти точку пересечения прямой А В с плоскостью, заданной
параллельными прямыми CD и EF (рис. 64).
§ 12. Пересечение плоскостей между собой
67*. Найти линию пересечения пл.Т, заданной следом Тv, с плоскостью, заданной двумя пересекающимися прямыми АВ и ВС (рис. 65, а).

Рис. 65а—в.
Решение. Как известно, построение линии пересечения двух плоскостей сво-
дится к нахождению двух точек, общих для обеих заданных плоскостей, или одной такой точки при известном направлении искомой линии.
В данном случае искомая прямая может быть определена, если найти точки пересечения прямых АВ и ВС с пл. Т (рис. 65,6). Следовательно, построение точек Kt и К2 сводится к показанному на рис. 59, б и в.

Рис.66
Если считать плоскости непрозрачными, то горизонтальные проекции участков прямых А В и ВС, находящихся под пл. Т, следует изображать штриховыми линиями.
Пл. Т не влияет на видимость прямых АВ и CD на пл. V, так как перпендикулярна к ней (рис. 65, в).
|
|
|
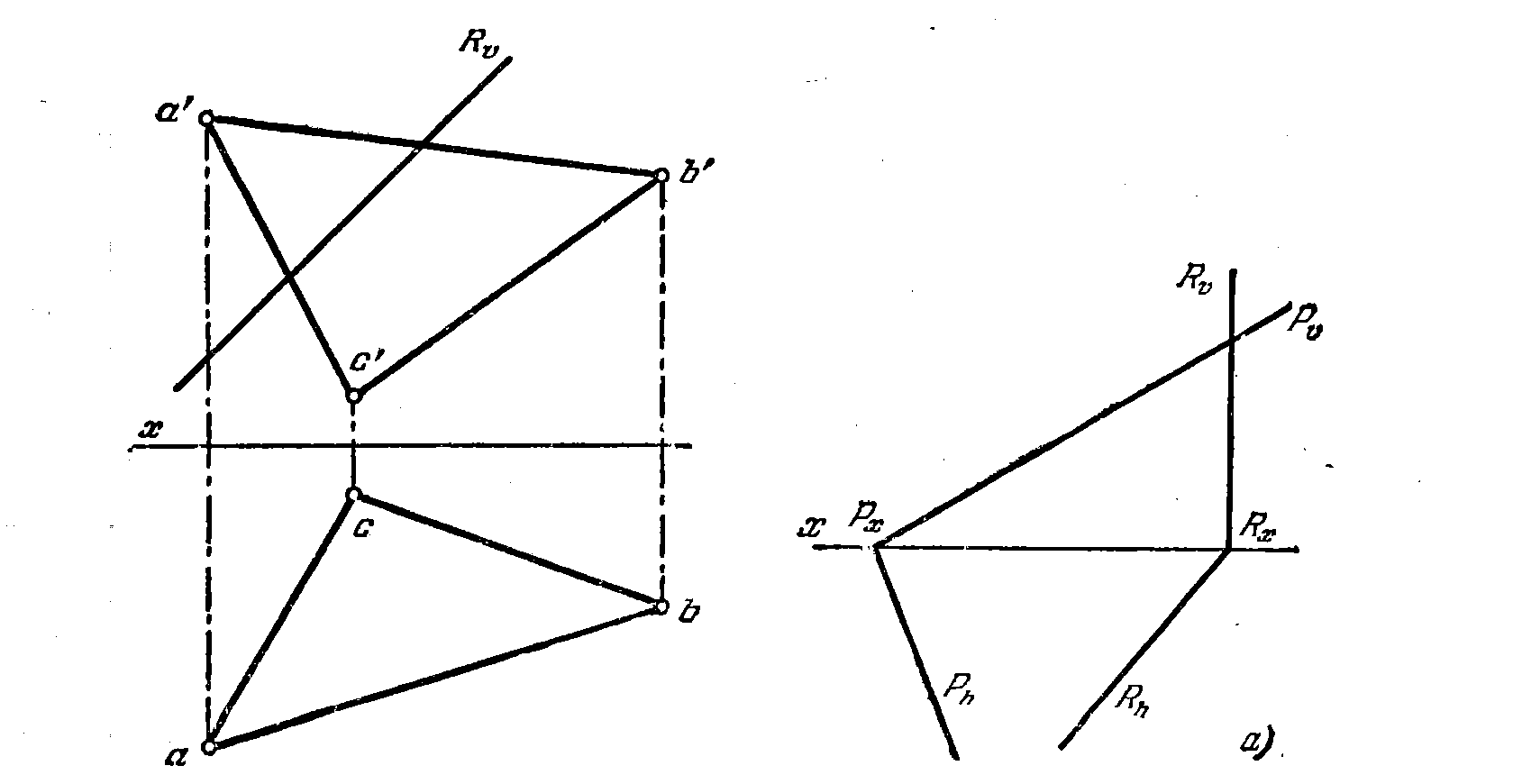
Рис.67 Рис. 68а.
вв. Найти линию пересечения пл. S, заданной следом Sh, с пло-
скостью, заданной параллельными прямыми АВ a CD (рис. 66).
69. Найти линию пересечения фронтально-проецирующей пл. R,
заданной следом Rv, с плоскостью, заданной треугольником ABC
(рис. 67).

Рис.68 б,в.
70*. Найти линию пересечения плоскостей Р и R (рис. 68, а).
Решение. Для построения линии пересечения плоскостей можно использо-
вать точку N пересечения следов Pv и Rv и точку М пересечения следов Рh и Rh (рис.68,б). Прямая МN, проходящая через эти точки, является искомой линией пересечения. Ее проекция mn совпадает со следом Rh, так как пл. R является горизонтально-проецирующей. Эти построения показаны на рис. 68, в.
71. Построить линию пересечения плоскостей Р и Q (рис. 69).

Рис.69
72. Построить линию пересечения плоскостей Р и Q (рис. 70).
Профильной плоскостью проекций не пользоваться.

Рис. 70.
73*. Построить линию пересечения плоскостей Р и Q, у которых
Ph ll Оh (рис. 71,а).
46 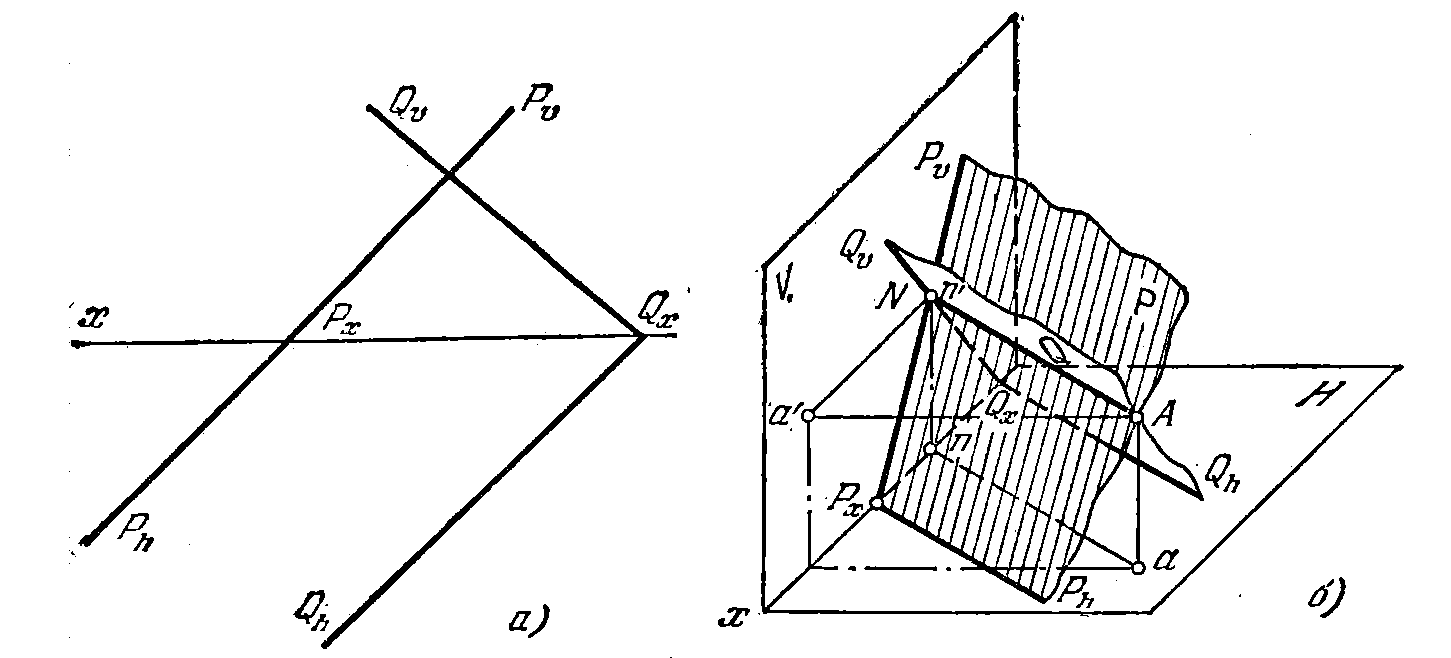
Рис. 71а, б.
|
|
|
Реше н и е. В данном случае горизонт, следы плоскостей параллельны. Это
значит что искомая прямая параллельна пл. Н и для плоскостей Р и Q является горизонталью (рис. 71, б). Чтобы провести эту горизонталь, достаточно построить одну принаплежащую ей точку. Используем точку N пересечения следов Pv и Qv. Построив проекции (рис. 71, в) n' и n, проводим nа' параллельно оси х, а nа — параллельно следам Ph и Qh.

Рис. 71в. Рис. 72.
74. Найти линию пересечения плоскостей Р и Q (рис. 72).
а) 
Рис. 73а, б.

Рис.73 в,г.
75*. Найти линию пересечения плоскостей Р и Q (рис. 73, а),
пользуясь профильной плоскостью проекций и не пользуясь ею.

Рис.74.
Р е щ е н и е. Так как заданные плоскости являются профильно-проецирующими,
то линия их пересечения МN (рис. 73, б) параллельна оси х. Чтобы найти эту прямую,надо построить одну принадлежащую ей точку. Вводим (рис. 73, б и в) вспомогательную плоскость S и строим линии пересечения ее с пл. Р (1—2) и Q (3—4). Эти линии, пересекаясь, дают точку М (m', m), общую для пл. Р и Q. Через m' и m проводим проекции искомой прямой m'n' и mn параллельно оси х. В качестве вспомогательной плоскости можно использовать и профильную плоскость проекций (рис. 73, б и г):
линия MN проходит через точку пересечения следов Pw и Qw.
76. Построить линию пересечения плоскостей треугольника ABC
и четырехугольника DEFG (рис. 74), пользуясь профильной плоско-
стью проекций и не пользуясь ею. Определить видимость плоскостей.
Дата добавления: 2018-02-18; просмотров: 1087; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
