ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПЛОСКОСТЬЮ
Тема: Решение позиционных задач по теме «Плоскость в ортогональных проекциях».
Цель занятий: Изучить способы задания плоскости и классификацию плоскостей, научится находить следы плоскости. Линии в плоскости. Взаимное положение и пересечение плоскостей. Научится решать позиционные задачи по данной теме.
Задание: Изучить краткие теоретические сведения и решить
задачи.
| Плоскость |
Плоскость – одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскость обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Некоторые характеристические свойства плоскости:
1. Плоскость есть поверхность, содержащая полностью каждую прямую, соединяющую любые ее точки;
2. Плоскость есть множество точек, равноотстоящих от двух заданных точек.
Плоскость в линейной алгебре - поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением 1-ой степени. Общее уравнение плоскости:
Ax+By+Cz+D=0,
где А, В, С, и D - постоянные, причем А, В и С одновременно не равны нулю.
| Способы графического задания плоскостей |
Положение плоскости в пространстве можно определить:
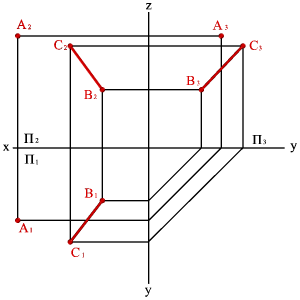
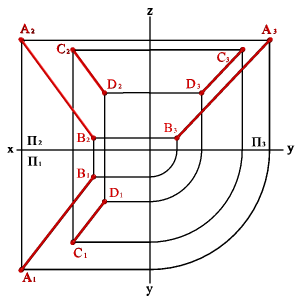
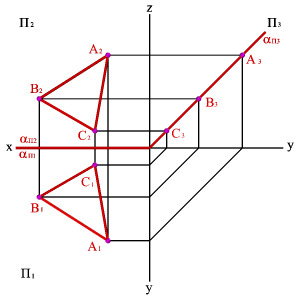
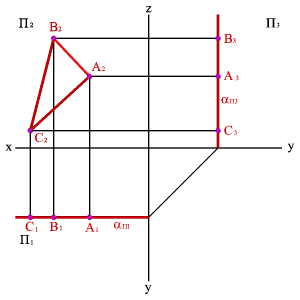
1. Тремя точками, не лежащими на одной прямой линии (рис.5.1);
|
| |||
| а) модель | 
| б) эпюр | ||
| Рисунок 5.1. Плоскость заданная тремя точками, не лежащими на одной прямой
| ||||
2. Прямой линией и точкой, не принадлежащей этой прямой (рис.5.2);
|
| |
| а) модель | 
| б) эпюр |
| Рисунок 5.2. Плоскость заданная прямой линией и точкой, не принадлежащей этой линии | ||
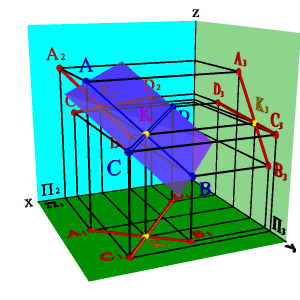
3. Двумя пересекающимися прямыми (рис.5.3);
|
| |
| а) модель | 
| б) эпюр |
| Рисунок 5.3. Плоскость заданная двумя пересекающимися прямыми линиями
| ||
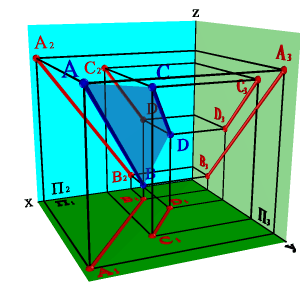
4. Двумя параллельными прямыми (рис.5.4);
|
| |
| а) модель | 
| б) эпюр |
| Рисунок 5.4. Плоскость заданная двумя параллельными прямыми линиями | ||

|
| Различное положение плоскости относительно плоскостей проекций |
В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
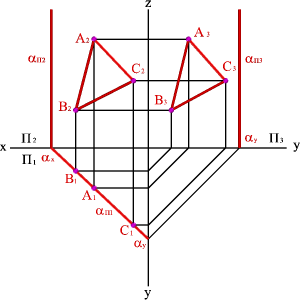
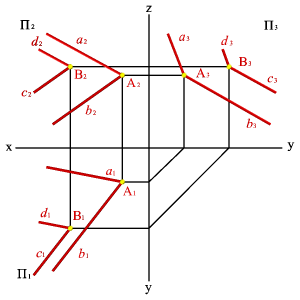
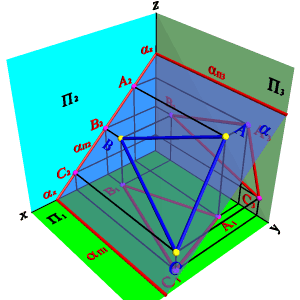
1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальный aП1; - фронтальный aП2; - профильный aП3).
Следы плоскости общего положения пересекаются попарно на осях в точках ax,ay,az. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций.
|
|
|
Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях (рис.5.5).
2.Плоскости перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:
2.1. Плоскость перпендикулярная горизонтальной плоскости проекций (^aP1), называется горизонтально проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек любых фигур в этой плоскости совпадают с горизонтальным следом (рис.5.6).

|
| |
| а) модель | 
| б) эпюр |
| Рисунок 5.6. Горизонтально проецирующая плоскость
| ||
2.2. Плоскость перпендикулярная фронтальной плоскости проекций (a^П2)- фронтально проецирующая плоскость. Фронтальной проекцией плоскости a является прямая линия, совпадающая со следом aП2 (рис.5.7).
|
| |
| а)модель | 
| б) эпюр |
| Рисунок 5.7. Фронтально проецирующая плоскость
| ||
2.3. Плоскость перпендикулярная профильной плоскости ( ^aП3) - профильно проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость (рис.5.8).
|
|
|

|
| |
| а) модель | 
| б) эпюр |
| Рисунок 5.8. Биссекторная плоскость | ||
3. Плоскости параллельные плоскостям проекций – занимают частное положение в пространстве и называются плоскостями уровня. В зависимости от того, какой плоскости параллельны исследуемая плоскость, различают:
3.1. Горизонтальная плоскость - плоскость параллельная горизонтальной плоскости проекций (aП1) - (^aП2,^aП3). Любая фигура в этой плоскости проецируется на плоскость П1 без искажения, а на плоскости П2 и П3 в прямые - следы плоскости aП2 и aП3 (рис.5.9).

|
| |
| а) модель | 
| б) эпюр |
| Рисунок 5.9. Горизонтальная плоскость
| ||
3.2. Фронтальная плоскость - плоскость параллельная фронтальной плоскости проекций (aП2), (a^П1, a^П3). Любая фигура в этой плоскости проецируется на плоскость П2 без искажения, а на плоскости П1 и П3 в прямые - следы плоскости aП1 и aП3 (рис.5.10).

|
| |
| а) модель | 
| б) эпюр |
| Рисунок 5.10. Фронтальная плоскость | ||
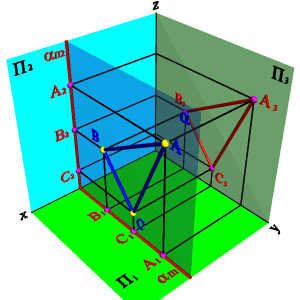
3.3. Профильная плоскость - плоскость параллельная профильной плоскости проекций (a//П3), (a^П1, a^П2).Любая фигура в этой плоскости проецируется на плоскость П3 без искажения, а на плоскости П1 и П2 в прямые - следы плоскости aП1 и aП2 (рис.5.11).
|
|
|
|
| |
| а) модель | 
| б) эпюр |
| Рисунок 5.11. Профильная плоскость | ||

|
| Следы плоскости |
Следом плоскости называется линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается данная, различают: горизонтальный, фронтальный и профильный следы плоскости.
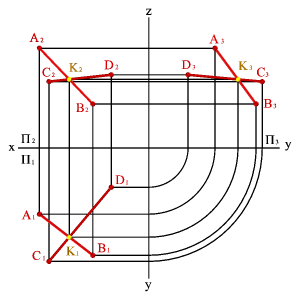
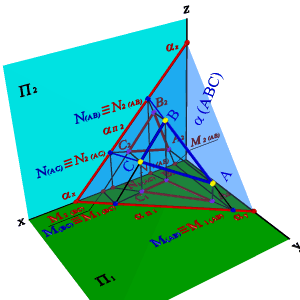
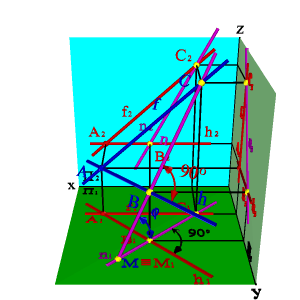
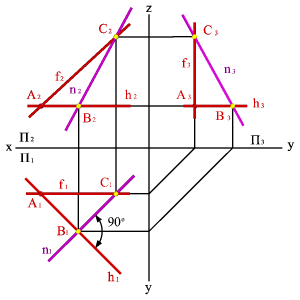
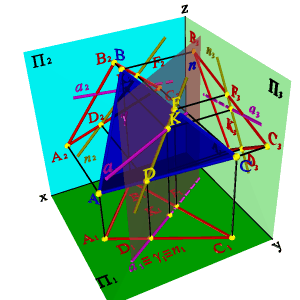
Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой( как для построения любой прямой). На рисунке 5.12 показано нахождение следов плоскости α(АВС).Фронтальный след плоскости αП2, построен, как прямая соединяющая две точки N(АС) иN(АВ), являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости α. Горизонтальный следαП1 – прямая, проходящая через горизонтальные следы прямых ВС и АВ. Профильный следαП3 – прямая соединяющая точки (αy и αz) пересечения горизонтального и фронтального следов с осями.
|
|
| ||

| а) модель | 
| б) эпюр |
| Рисунок 5.12. Построение следов плоскости
| |||
| Взаимное расположение прямой и плоскости |
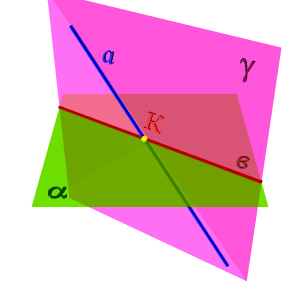
Определение взаимного положения прямой и плоскости - позиционная задача, для решения которой применяется метод вспомогательных секущих плоскостей. Сущность метода заключается в следующем: через прямую проведем вспомогательную секущую плоскость gи установим относительное положение двух прямых а и в,последняя из которых является линией пересечения вспомогательной секущей плоскости g и данной плоскости a(рис.5.13).
|
| Каждому из трех возможных случаев относительного расположения этих прямых соответствует аналогичный случай взаимного расположения прямой и плоскости. Так, если обе прямые совпадают, то прямаяа лежит в плоскости a, параллельность прямых укажет на параллельность прямой и плоскости и, наконец, пересечение прямых соответствует случаю когда прямая а пересекает плоскость a. Таким образом возможны три случая относительного расположения прямой и плоскости: · Прямая принадлежит плоскости; · Прямая параллельна плоскости; · Прямая пересекает плоскость, частный случай – прямая перпендикулярна плоскости. Рассмотрим каждый случай. | |

| Рисунок 5.13. Метод вспомогательных секущих плоскостей | |
| Прямая линия, принадлежащая плоскости |
Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат той же плоскости (рис.5.14).
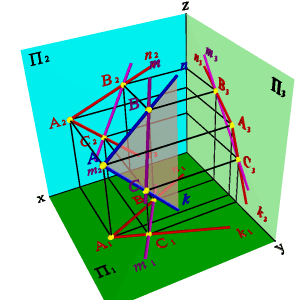
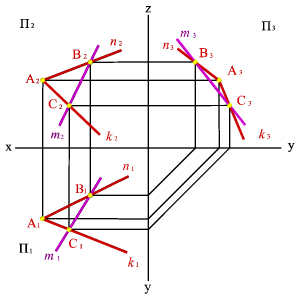
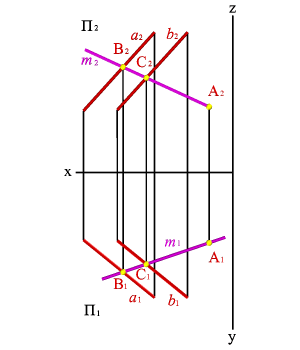
Задача. Дана плоскость (n,k) и одна проекция прямой m2.
Требуется найти недостающие проекции прямой m если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k.
Проекция прямой m2 пересекает прямые n и k в точках В2 и С2, для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек лежащих на прямых соответственно n и k.
Таким образом точки В и С принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит согласно аксиоме прямая принадлежит этой плоскости.
|
|
| ||||

| а) модель | 
| б) эпюр | ||
| Рисунок 5.14. Прямая и плоскость имеют две общие точки | |||||
Аксиома 2.Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости (рис.5.15).
Задача.
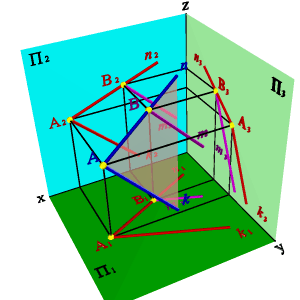
Через точку В провести прямую m если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k.
Пусть В принадлежит прямой n лежащей в плоскости заданной пересекающимися прямыми n и k. Через проекцию В2 проведем проекцию прямой m2 параллельно прямой k2, для нахождения недостающих проекций прямой необходимо построить проекцию точки В1, как точки лежащей на проекции прямой n1 и через неё провести проекцию прямой m1 параллельно проекции k1.
Таким образом точки В принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k, значит согласно аксиоме прямая принадлежит этой плоскости.
|
|
| ||

| а) модель | 
| б) эпюр |
| Рисунок 5.15. Прямая имеет с плоскостью одну общую точку и параллельна прямой расположенной в этой плоскости | |||
| Главные линии в плоскости |
Среди прямых линий, принадлежащих плоскости, особое место занимают прямые, занимающие частное положение в пространстве:
1. Горизонтали h - прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (hÎСВА, hP1, h2Ох,h3Оy)(рис.5.16).
|
|
| ||

| а) модель | 
| б) эпюр |
| Рисунок 5.16. Горизонталь
| |||
2. Фронтали f - прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (fÎСВА, fP2, f1Ох, f3Оz)(рис.5.17).
|
|
| ||

| а) модель | 
| б) эпюр |
| Рисунок 5.17. Фронталь
| |||
3. Профильные прямые р - прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (рÎСВА, рP3, р1^Ох, р2^Ох)(рис.5.18).
|
|
| ||

| а) модель | 
| б) эпюр |
| Рисунок 5.18. Профильная прямая
| |||
Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости.
4. Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j , которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.5.19).
|
|
| ||

| а) модель | 
| б) эпюр |
| Рисунок 5.19. Линия наибольшего ската | |||
Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.

|
| Прямая линия, параллельная плоскости |
При решении вопроса о параллельности прямой линии и плоскости необходимо опираться на известное положение стереометрии: прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскостии не принадлежит этой плоскости.
Задача. Дано: проекции плоскости общего положения ABC и прямой общего положения а.
Требуется оценить их взаимное положение (рис.5.20).
|
|
| ||

| а) модель | 
| б) эпюр |
| Рисунок 5.20. Прямая параллельная плоскости | |||
Для этого через прямую а проведем вспомогательную секущую плоскость g - в данном случае горизонтально проецирующая плоскость. Найдем линию пересечения плоскостей g и АВС- прямую п (DF). Проекция прямой п на горизонтальную плоскость проекций совпадает с проекцией а1 и со следом плоскости g. Проекция прямой п2 параллельна а2, п3 параллельна а3, следовательно, прямая а параллельна плоскости AВС.
| sexy Moscow Escorts with pics Прямая линия, пересекающая плоскость |
Нахождение точки пересечения прямой линии и плоскости – основная задача начертательной геометрии.
Задача. Дано: плоскость AВС и прямая а.
Требуется найти точку пересечения прямой с плоскостью и определить видимость прямой по отношению к плоскости.
Для решения задачи:
1. Через горизонтальную проекцию прямой а1 проведем вспомогательную горизонтально проецирующую плоскость g (таким образом а g Î).
2. Горизонтальный след плоскости g1 пересекает проекцию плоскости A1В1С1 в точках D1 и F1, которые определяют положение горизонтальной проекции п1- линии пересечения плоскостей g и AВС. Для нахождения фронтальной и профильной проекции п спроецируем точки D и F на фронтальную и профильную плоскости проекций.
3. На фронтальной и профильной проекциях линия пересечения плоскостей п пересекает проекции а в точке К, которая и является проекцией точки пересечения прямой а с плоскостью AВС, по линии связи находим горизонтальную проекцию К1.
4. Методом конкурирующих точек определяем видимость прямой а по отношению к плоскости AВС.
|
|
| ||

| а) модель | 
| б) эпюр |
| Рисунок 5.21. Нахождение точки пересечения прямой и плоскости | |||
Таким образом алгоритм решения задачи состоит из следующей последовательности действий (рис.5.21):
1. Построение вспомогательной секущей плоскости g ( горизонтально – проецирующая плоскость), которую проводят через прямую а (а)gÎ;
2. Построение линии пересечения вспомогательной плоскости g и заданной плоскости a (п)gÇa=;
3. Определение искомой точки К, как точки пересечения двух прямых, заданной - а и полученной в результате пересечения плоскостей – п (К=а Ç п). В качестве вспомогательной плоскости g рекомендуется брать одну из проецирующих плоскостей.
4. Определение видимости прямой аотносительно плоскости a.
| Прямая линия перпендикулярная плоскости. |
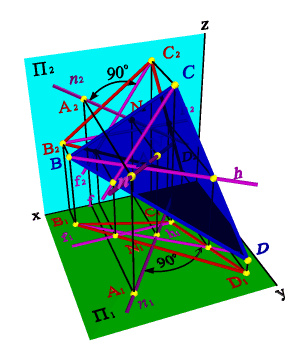
Докажем следующую теорему о перпендикуляре к плоскости: Если прямая перпендикулярна плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция – фронтальной проекции фронтали плоскости.
Пусть прямая n,перпендикулярная плоскости, пересекает плоскость BCD в точке N, тогда по условию nперпендикулярна любой прямой плоскости. Проведем в плоскости BCDгоризонтальh, а на основании теоремы о проецировании прямого угла можно утверждать, что на горизонтальную плоскость проекций они проецируются под прямым углом, т.е. n1 ^h1. Аналогично для фронтали – f ^ n Þ f2 ^ n2.
Справедлива и обратная теорема: Если проекции прямой перпендикулярны одноименным проекциям соответствующих главных линий плоскости (горизонтали и фронтали), то такая прямая перпендикулярна плоскости.
Доказательство следует из теоремы о проецировании прямого угла.
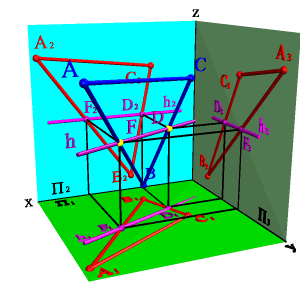
Исходя из рассмотренных теорем, можно решить задачу о построении перпендикуляра к плоскости из точки А (рис.5.22).
Задача. Дано: плоскость ВСDи точка А.
Требуетсяпостроить прямую линию n проходящую через точку А и перпендикулярную плоскости ВСD.
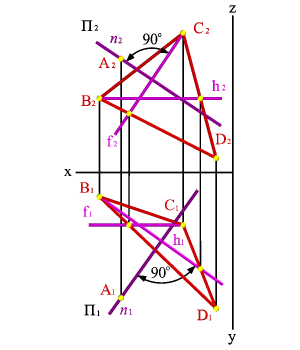
В плоскости ВСD построим фронталь f и горизонталь h. В горизонтальной плоскости проекций проведем через точку А1 прямую n1 перпендикулярно горизонтальной проекции горизонтали h1, а на фронтальной плоскости проекций через точку А2 прямую n2 перпендикулярно фронтальной проекции фронтали f2, согласно выше сказанному полученная прямая n будет перпендикулярна плоскости ВСD.
|
|
| ||

| а) модель | 
| б) эпюр |
| Рисунок 5.22. Построение прямой, перпендикулярной плоскости | |||
| Взаимное расположение точки и плоскости |
Возможны два варианта взаимного расположения точки и плоскости: либо точка принадлежит плоскости, либо нет.
Если точка принадлежит плоскости то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну.
Рассмотрим пример (рис.5.23): Построение проекции точки А принадлежащей плоскости общего положения заданной двумя параллельными прямыми a(ab).
Задача. Дано: плоскость a(а,в)и проекция точки А2.
Требуетсяпостроить проекцию А1 если известно, что точка А лежит в плоскости в,а.
Через точку А2 проведем проекцию прямой m2, пересекающую проекции прямых a2и b2 в точках С2 и В2 (С,aÎ BaÎ Þ maÎ). Построив проекции точек С1 и В1, определяющие положение m1, находим горизонтальную проекцию точки А (А1Î m1, maÎ Þ АaÎ).
|
|
| ||

| а) модель | 
| б) эпюр |
| Рисунок 5.23. Точка, принадлежащая плоскости | |||
Через точку А2 проведем проекцию прямой m2, пересекающую проекции прямых a2и b2 в точках С2 и В2 (СÎ,aBÞaÎmaÎ). Построив проекции точек С1 и В1, определяющие положение m1, находим горизонтальную проекцию точки А (А1Î m1, m ÞaÎ АaÎ).

|
| Взаимное расположение точки и плоскости |
Возможны два варианта взаимного расположения точки и плоскости: либо точка принадлежит плоскости, либо нет.
Если точка принадлежит плоскости то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну.
Рассмотрим пример (рис.5.23): Построение проекции точки А принадлежащей плоскости общего положения заданной двумя параллельными прямыми a(ab).
Задача. Дано: плоскость a(а,в)и проекция точки А2.
Требуетсяпостроить проекцию А1 если известно, что точка А лежит в плоскости в,а.
Через точку А2 проведем проекцию прямой m2, пересекающую проекции прямых a2и b2 в точках С2 и В2 (С,aÎ BaÎ Þ maÎ). Построив проекции точек С1 и В1, определяющие положение m1, находим горизонтальную проекцию точки А (А1Î m1, maÎ Þ АaÎ).
|
|
| ||

| а) модель | 
| б) эпюр |
| Рисунок 5.23. Точка, принадлежащая плоскости | |||
Через точку А2 проведем проекцию прямой m2, пересекающую проекции прямых a2и b2 в точках С2 и В2 (СÎ,aBÞaÎmaÎ). Построив проекции точек С1 и В1, определяющие положение m1, находим горизонтальную проекцию точки А (А1Î m1, m ÞaÎ АaÎ).
| Взаимное расположение двух плоскостей |
Две плоскости в пространстве могут быть либо взаимно параллельны, в частном случае совпадая друг с другом, либо пересекаться. Взаимно перпендикулярные плоскости представляют собой частный случай пересекающихся плоскостей.
1. Параллельные плоскости. Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Это определение хорошо иллюстрируется задачей, через точку В провести плоскость параллельную плоскости, заданной двумя пересекающимися прямыми ab (рис.5.24).
Задача. Дано: плоскость общего положения, заданную двумя пересекающимися прямыми ab и точка В.
Требуется через точку В провести плоскость, параллельную плоскости ab и задать её двумя пересекающимися прямыми c и d.
Согласно определения если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости то эти плоскости параллельны между собой.
Для того чтобы провести на эпюре параллельные прямые необходимо воспользоваться свойством параллельного проецирования - проекции параллельных прямых - параллельны между собой
d//a, с//b Þ d1a1,с1//b1; d2a2 ,с2//b2; d3a3,с3//b3.
|
|
| ||

| а) модель | 
| б) эпюр |
| Рисунок 5.24. Параллельные плоскости | |||
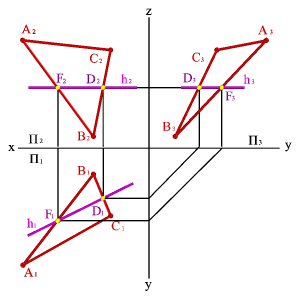
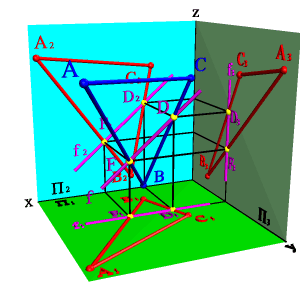
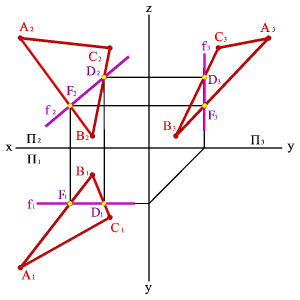
2. Пересекающиеся плоскости, частный случай – взаимно перпендикулярные плоскости. Линия пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей.
Рассмотрим построение линии пересечения двух плоскостей, когда одна из них проецирующая (рис.5.25).
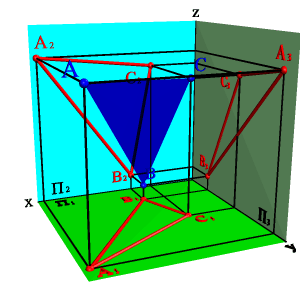
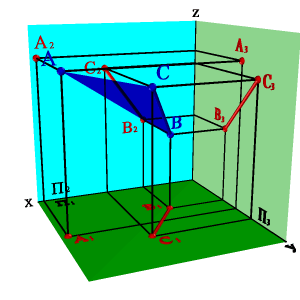
Задача. Дано: плоскость общего положения задана треугольником АВС, а вторая плоскость - горизонтально проецирующая a.
Требуется построить линию пересечения плоскостей.
Решение задачи заключается в нахождении двух точек общих для данных плоскостей, через которые можно провести прямую линию. Плоскость, заданная треугольником АВС можно представить, как прямые линии (АВ), (АС), (ВС). Точка пересечения прямой (АВ) с плоскостью a - точка D, прямой (AС) -F. Отрезок [DF] определяет линию пересечения плоскостей. Так как a - горизонтально проецирующая плоскость, то проекция D1F1 совпадает со следом плоскости aП1,таким образом остается только построить недостающие проекции [DF] на П2 и П3.
|
|
| ||

| а) модель | 
| б) эпюр |
| Рисунок 6.25. Пересечение плоскости общего положения с горизонтально проецирующей плоскостью | |||
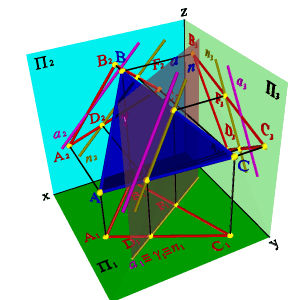
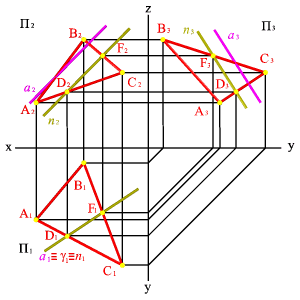
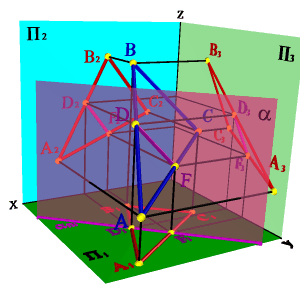
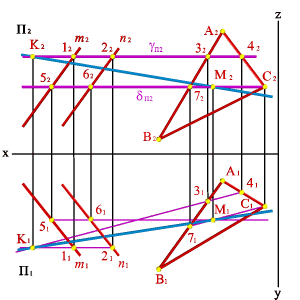
Перейдем к общему случаю. Пусть в пространстве заданы две плоскости общего положения a(n,m) и b (ABC) (рис.5.26).
|
|
| ||

| а) модель | 
| б) эпюр |
| Рисунок 5.26. Пересечение плоскостей общего положения | |||
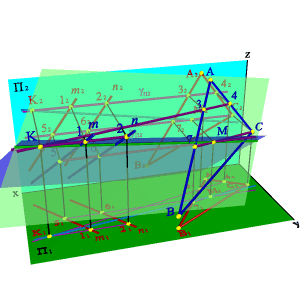
Рассмотрим последовательность построения линии пересечения плоскостей a(m//n) и b(АВС).По аналогии с предыдущей задачей для нахождения линии пересечения данных плоскостей проведем вспомогательные секущие плоскости g и d. Найдем линии пересечения этих плоскостей с рассматриваемыми плоскостями. Плоскость g пересекает плоскость a по прямой (12), а плоскость b - по прямой (34). Точка К - точка пересечения этих прямых одновременно принадлежит трем плоскостям a, b и g, являясь таким образом точкой принадлежащей линии пересечения плоскостей a и b. Плоскость d пересекает плоскости a и b по прямым (56) и (7C) соответственно, точка их пересечения М расположена одновременно в трех плоскостях a, b, d и принадлежит прямой линии пересечения плоскостей a и b. Таким образом найдены две точки принадлежащие линии пересечения плоскостей a и b - прямая (КМ).
Некоторого упрощения при построении линии пересечения плоскостей можно достичь, если вспомогательные секущие плоскости проводить через прямые, задающие плоскость.
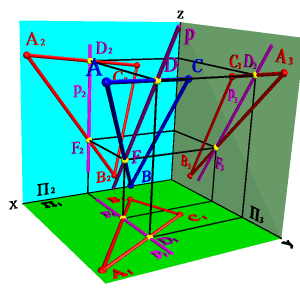
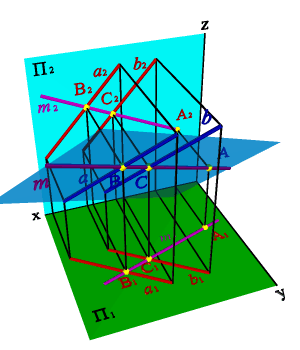
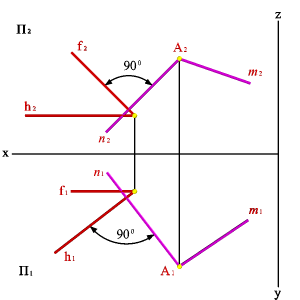
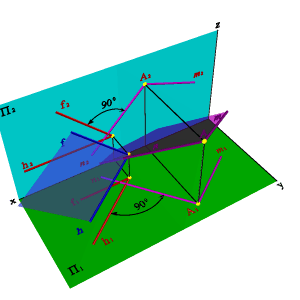
Взаимно перпендикулярные плоскости. Из стереометрии известно, что две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Через точку А можно провести множество плоскостей перпендикулярных данной плоскости a(f,h). Эти плоскости образуют в пространстве пучок плоскостей, осью которого является перпендикуляр опущенный из точки А на плоскость a . Для того чтобы из точки А провести плоскость перпендикулярную плоскости заданной двумя пересекающимися прямыми hf необходимо из точки А провести прямую n перпендикулярную плоскости hf (горизонтальная проекция n перпендикулярна горизонтальной проекции горизонтали h, фронтальная проекция n перпендикулярна фронтальной проекции фронтали f). Любая плоскость проходящая через прямую n будет перпендикулярна плоскости hf, поэтому для задания плоскости через точки А проводим произвольную прямую m. Плоскость заданная двумя пересекающимися прямыми mn будет перпендикулярна плоскости hf (рис.5.27).
|
| |
| а) модель | 
| б) эпюр |
| Рисунок 5.27. Взаимно перпендикулярные плоскости | ||
ЗАДАЧИ.
Плоскость
Прямая и точка в плоскости
40*. В плоскости, заданной точками А, В и С, провести горизон-
горизонталь на расстоянии / от пл. проекций Н (рис. 38, а).
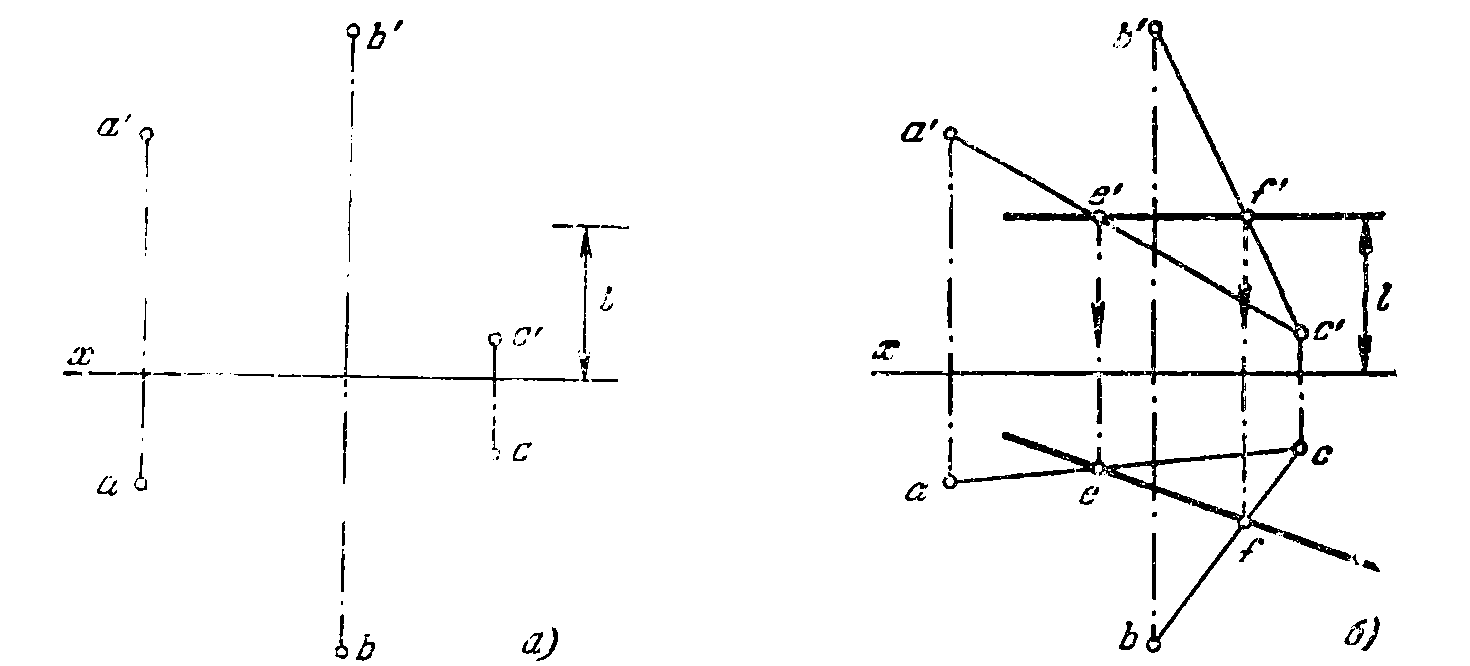
Рис. 38а, б.
Решение. Переходим от задания плоскости тремя точками к заданию ее
двумя прямыми АС и ВС (рис. 38, б). Проводим фронт, проекцию искомой горизонтали на расстоянии l от оси х. Отмечаем точки е' и f' на проекциях а' с ' и Ь' с' и находим проекции е и f на а с и b c. Горизонт, проекция искомой прямой проходит через точки е и f.
41. Провести через точку С горизонталь плоскости, заданной
прямой АВ п точкой С (рис. 39).
42*. В плоскости, заданной пересекающимися прямыми АВ и
CD, провести через точку К фропталь (рис. 40, а).
Решение. Так как направление горизонт, проекции фронтали известно, то
начинаем построение с проведения этой проекции через точку к: прямая km должна быть параллельна оси х (рис. 40, б). Чтобы построить фронт, проекцию искомой фронтали, надо построить фронт, проекцию какой-либо точки, принадлежащей фронтали. Выбираем на проекции фронтали произвольную точку е, проводим через нее горизонт, проекцию с f некоторой прямой, лежащей в заданной плоскости. Строим далее точку f'
на прямой а'Ь', проводим c'f' и находим на ней точку e'. Фронт, проекция искомой фронтали проходит через точки k' и с'.

Рис.39. Рис.40 а.
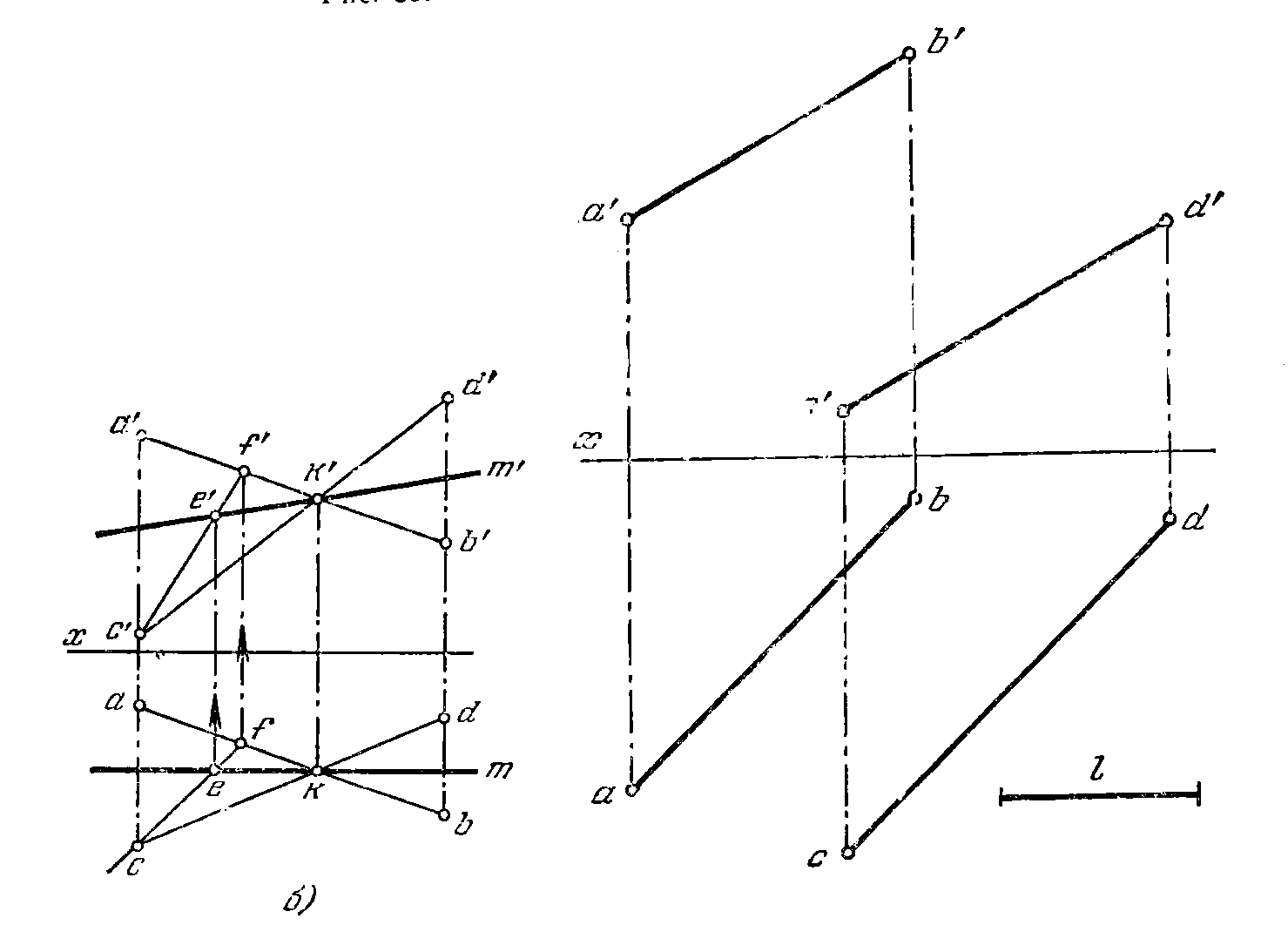
Рис.40 б. Рис.41
43. В плоскости, заданной параллельными прямыми АВ и CD,
провести фронталь на расстоянии / от пл. проекций V (рис. 41).
44*. В плоскости, заданной прямой А В и точкой С, провести
через точку А линию ската плоскости (рис. 42, я).
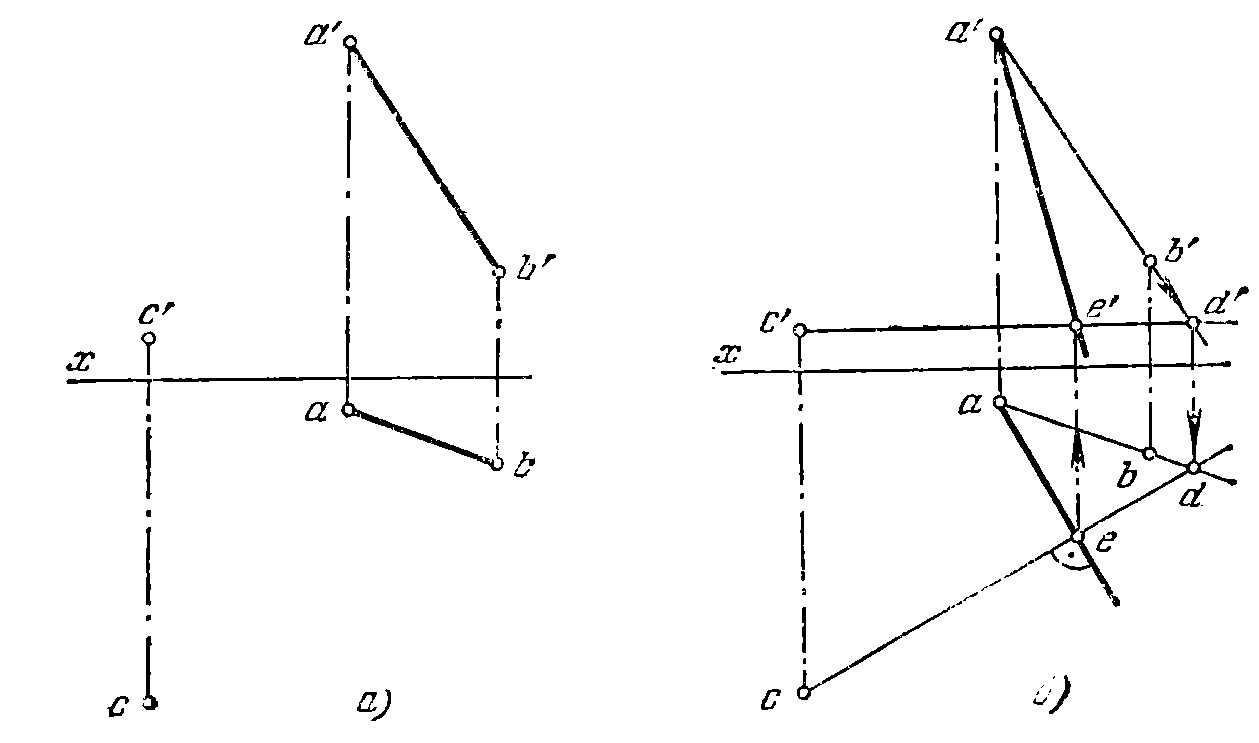
Рис. 42л, б.
Решение. Как известно, линия ската перпендикулярна к любой горизонтали
плоскости. Горизонт, проекции, линии ската и горизонтали взаимно
перпендикулярны. На рис. 42, б проведена горизонталь через точку С, сначала получена точка d', а по ней точка d на продолженной проекции a b. Таким образом, получена проекция cd горизонтали СD.Через точку а проводим горизонт, проекцию линии ската до пересечения с прямой cd в точке е, находим е' на с'd' и проекцию а' е' искомой линии ската.

Рис. 43.
45. В плоскости, заданной параллельными прямыми А В и CD,
провести через точку В линию ската (рис. 43).
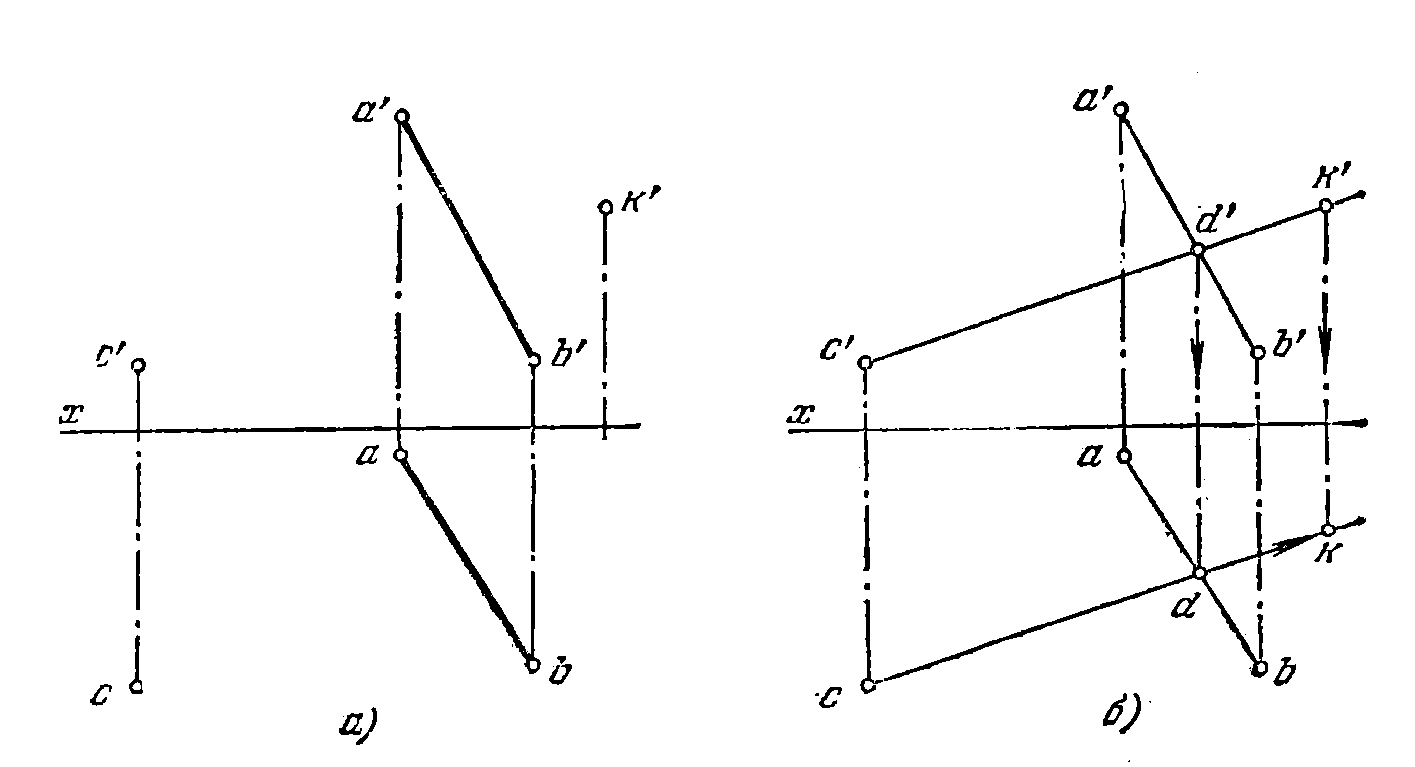
Рис. 44а, б.
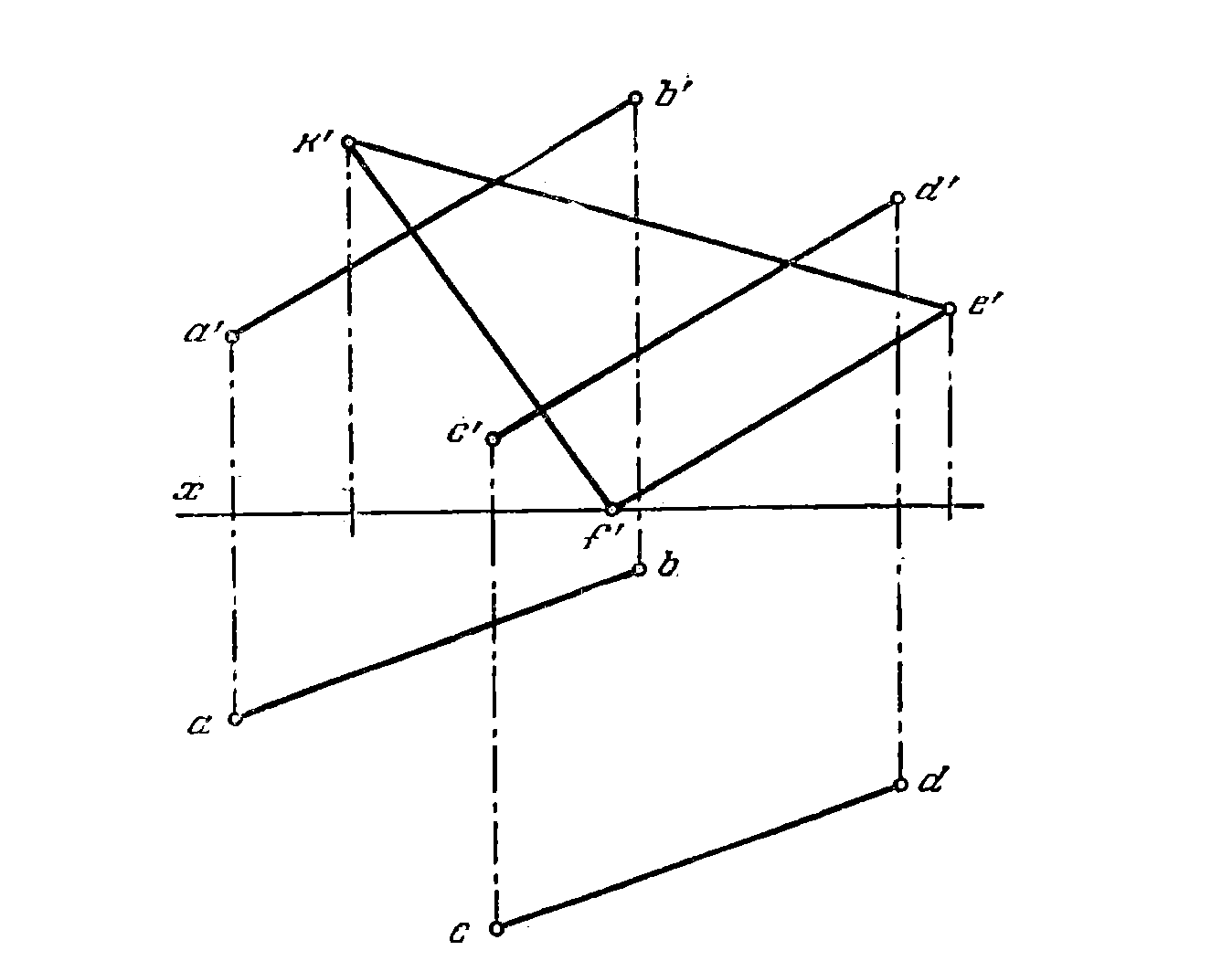
Рис. 45.
46*. Найти недостающую проекцию точки К, лежащей в плоскости, заданной прямой АВ и точкой С (рис. 44, а).
Решение. Известно, что если точка принадлежит плоскости, то она
принадлежит какой-либо прямой этой плоскости. Поэтому через точки с' и k' (рис. 44, б) проводим фронт, проекцию вспомогательной прямой, лежащей в данной плоскости.
Получив точку d', находим точку d на проекции аb. Теперь проводим прямую из точки с через точку d и на этой прямой находим горизонт, проекцию точки К.
47. Построить недостающую проекцию треугольника KEF, лежа-
лежащего в плоскости, заданной параллельными прямыми АВ и CD
(рис. 45).
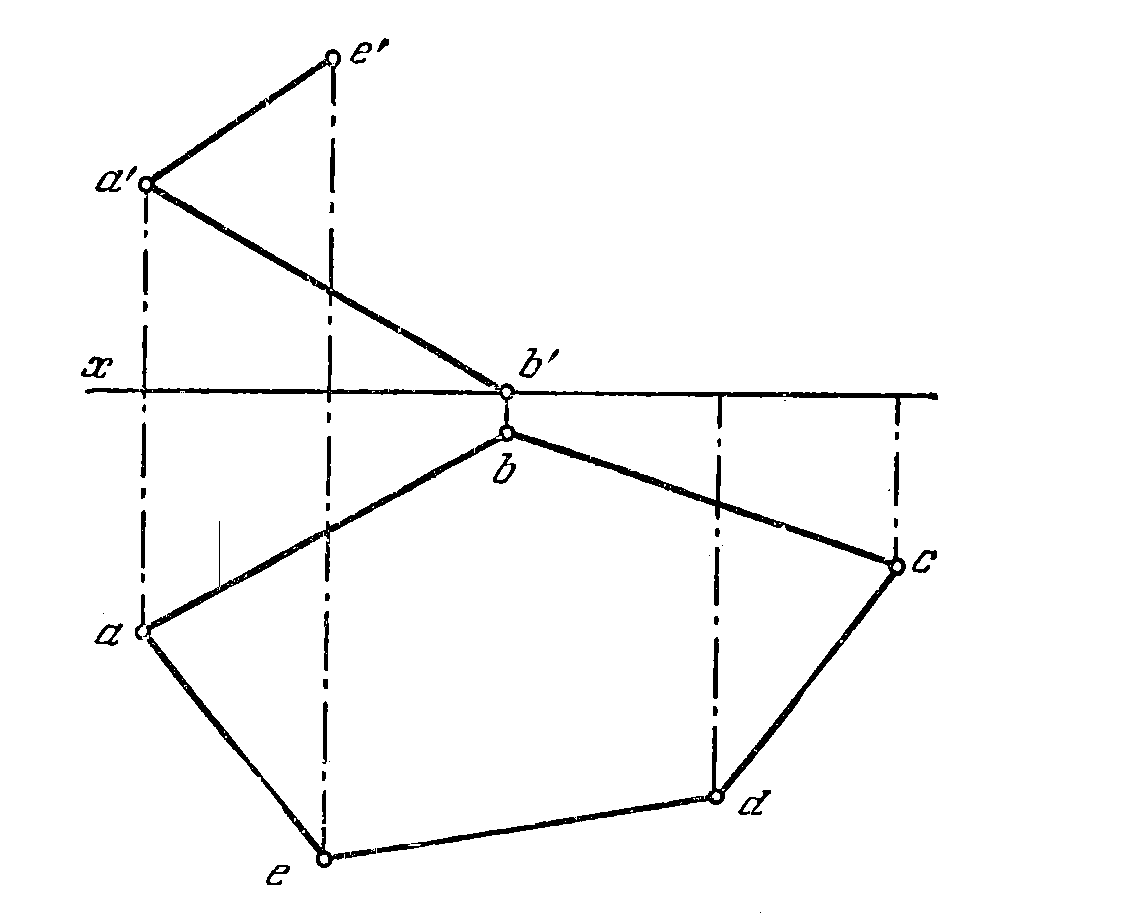
Рис. 46
48. Построить фронт, проекцию плоского пятиугольника
ABCDE по заданной его горизонт, проекции и фронтальным проекциям двух смежных сторон (рис. 46).
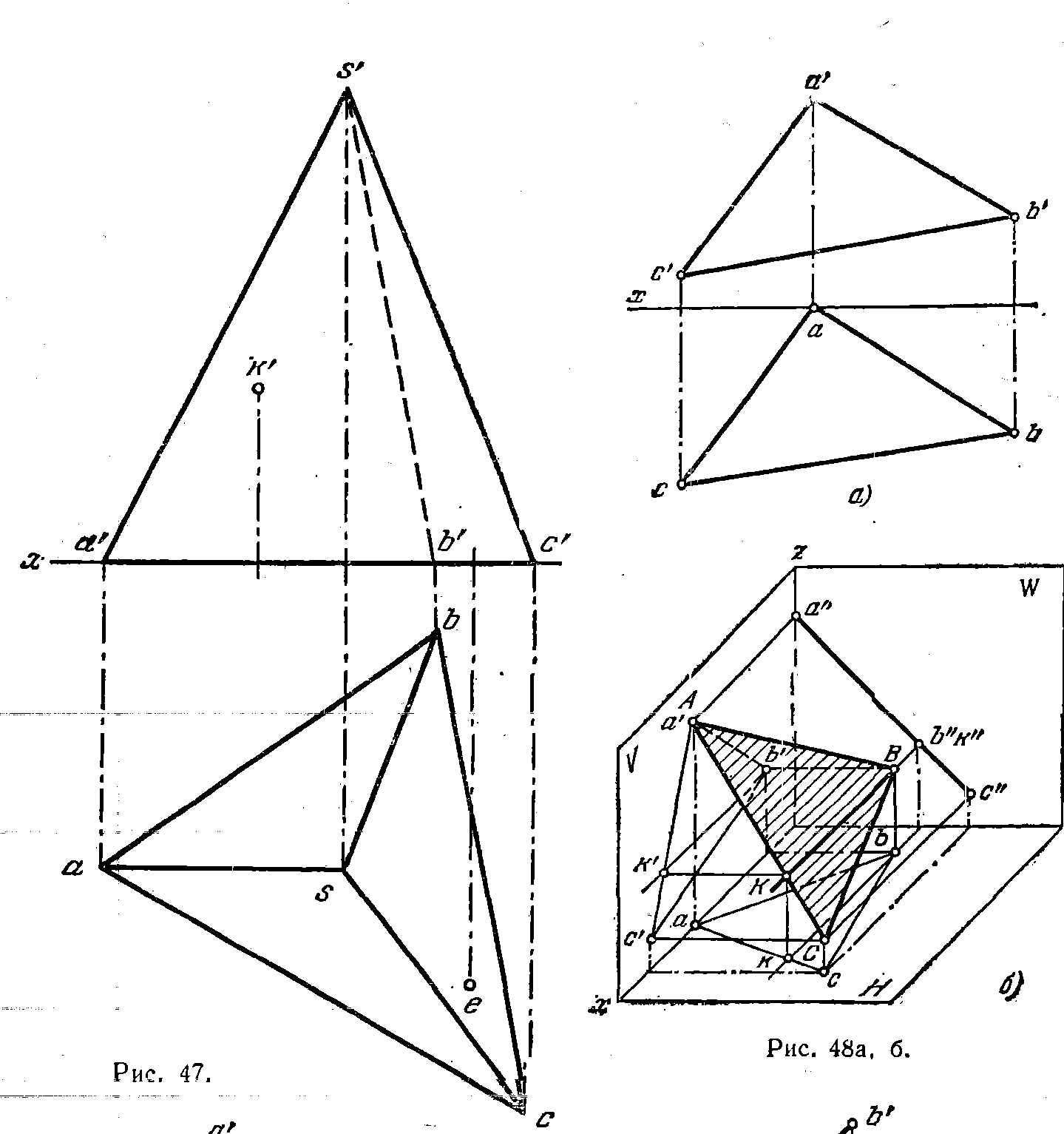
49. Дана пирамида SABC (рис. 47).
1) Найти горизонт, проекцию точки К, лежащей на грани SAC.
2) Найти фронт, проекцию точки Е, лежащей на грани SBC.
50*. Определить расположение плоскости, заданной треугольником ABC, относительно плоскостей проекций V, Н и W (рис. 48, а).
Решение. Заданная плоскость, как видим, не перпендикулярна ни к пл. V,
ни к пл. Н, так как ни на одной из этих плоскостей она не изображается в виде прямой линии. Следовательно, плоскость треугольника ABC является или плоскостью общего положения, пли профильно-проецирующей. Но если плоскость профильно-проецирующая (т. е. расположена перпендикулярно к пл. W), то она должна проходить через перпендикуляр к W (рис. 48,6). Посмотрим, можно ли провести в ABC перпендикуляр к W. Оказывается, можно (рис. 48, в): им служит хотя бы горизонталь KB (являющаяся в то же время фронталью ). Построение начинаем с проведения фронт, проекции
b'k' горизонтали, затем находим горизонт, проекцию bk. Так как bk ll b'k' (конечно,в пределах графической точности чертежа), то прямая ВК, а следовательно, и плоскость ABC перпендикулярны к пл. W.
Мы здесь обошлись без построения профильной проекции треугольника ABC.
Конечно, можно было начать с ее построения: если она оказалась бы отрезком прямой, то этим устанавливалось бы, что плоскость ABC профильно-проецирующая.
51. Определить расположение плоскости, заданной двумя
параллельными прямыми, относительно плоскостей проекций V, Н и W
(рис. 49).
§ 10. Следы плоскости
52*. Построить следы плоскости, заданной параллельными пря-
прямыми А В и CD (рис. 50, а).
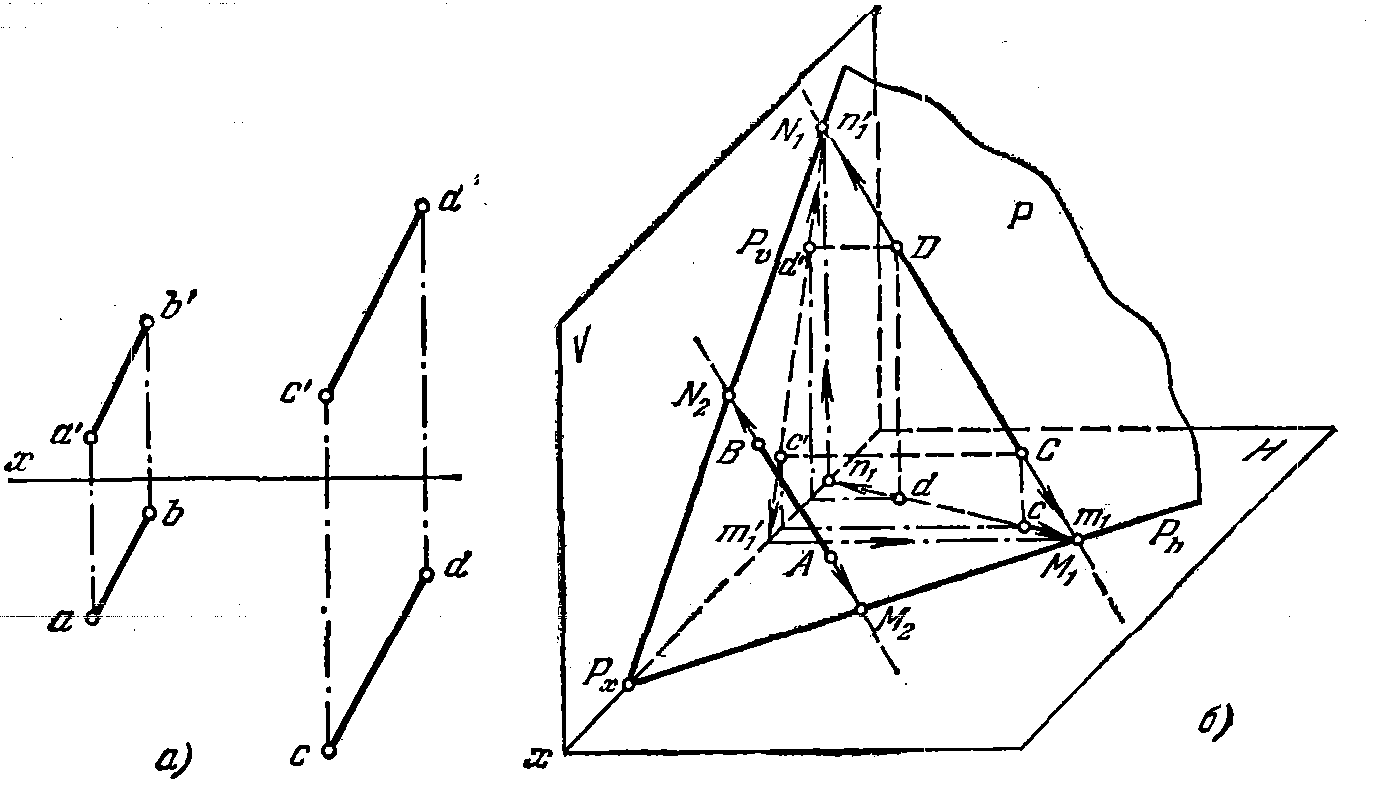
Рис. 50а, б.
Решение. Если прямая лежит в плоскости, то следы прямой лежат на одно-
одноименных с ними следах плоскости (рис. 50, б). Чтобы построить следы заданной плоскости, надо построить следы прямых АВ и CD. Фронт, след Рv пройдет через фронт, следы прямых, т. е. через точки N1, и N2, а горизонтальный — через следы M1 и М2.
Строим следы прямых АВ и CD, как это рассмотрено в § 4 (например, задача 12*). Через точки m1 и m2 проходит горизонт, след Рh, а через точки n'1 и n'2 — след Pv (рис. 50, в). Если построение выполнено точно, то оба следа пересекаются в точке Рх на оси х.
53. Построить следы плоскости, заданной двумя пересекающимися прямыми АВ и АС (рис. 51).
54*. Построить следы плоскости, заданной двумя пересекающимися прямыми АВ (АВ || пл. Н) и CD (рис. 52, а).
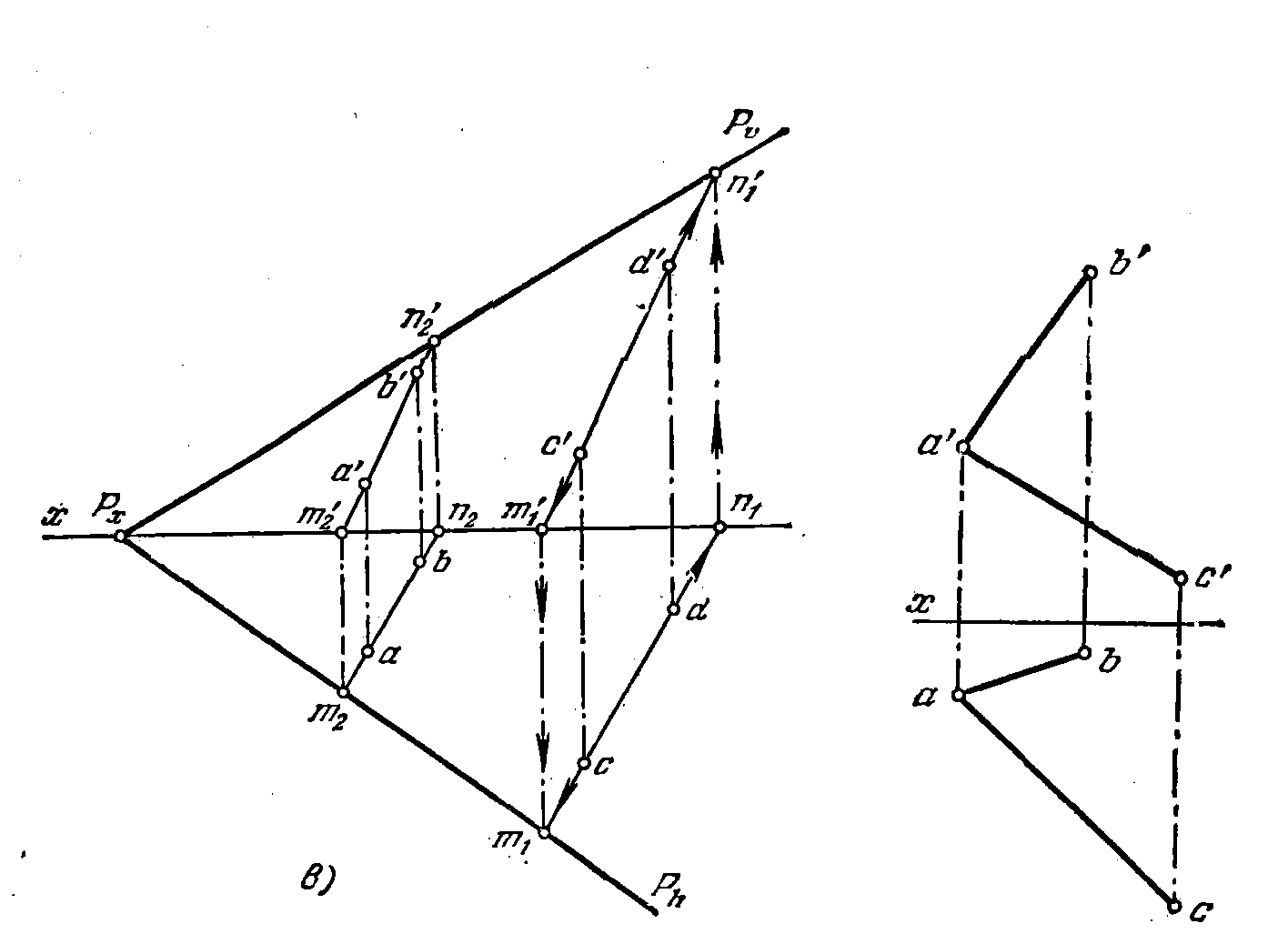
Рис. 50в. Рис. 51.
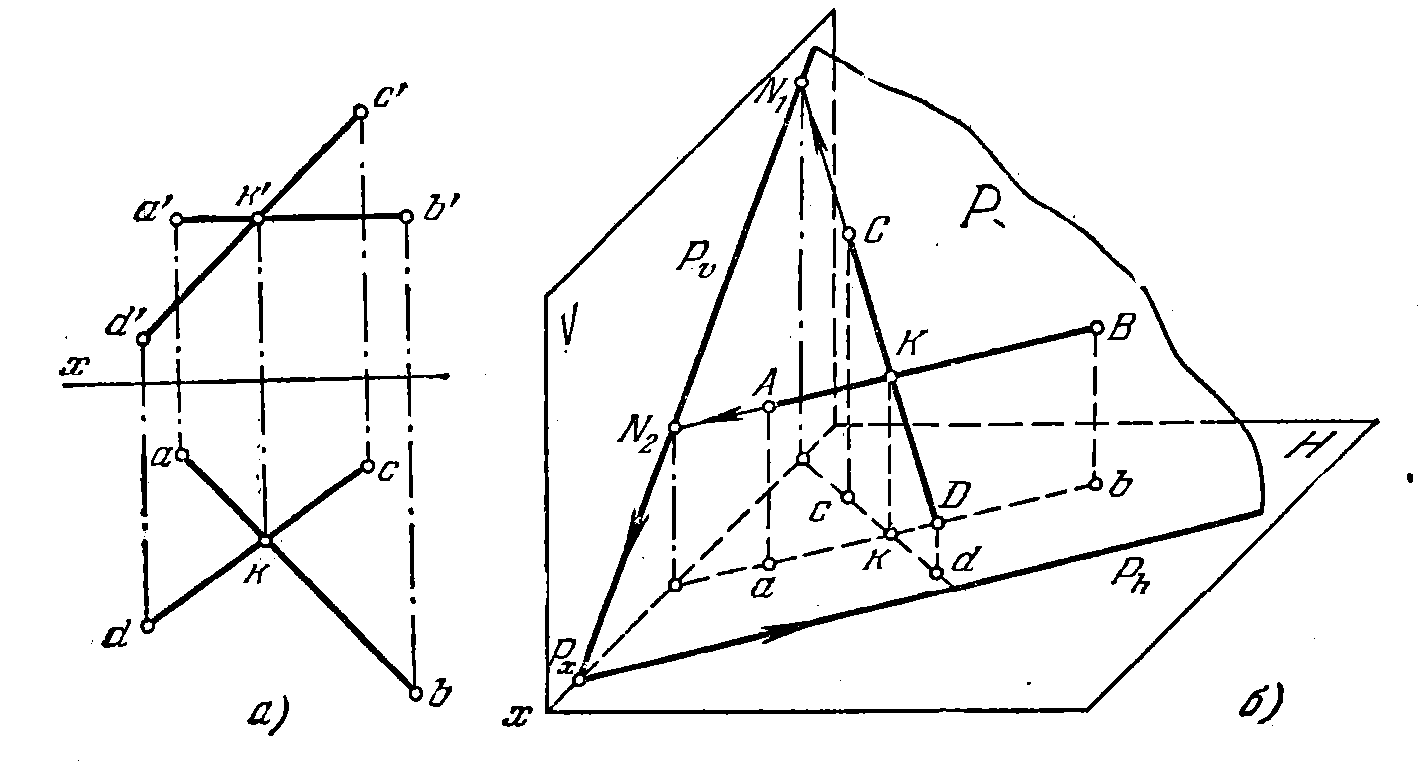
Рис. 52а, б.
Решение. Так как следы плоскости должны проходить через одноименные
с ними следы прямых, лежащих в этой плоскости (рис. 52, б), то надо построить фронт, следы обеих прямых — точки N2 и N1 и провести через них фронт, след плоскости (Pv). Направление горизонт, следа плоскости известно: след Ph должен быть параллелен горизонтали АВ (рис. 52, б). Поэтому след Ph пройдет через точку пересечения следов (Рх) параллельно горизонтали А В. На рис. 52, в показано, что проекции ab и cd продолжены до пересечения их с осью х в точках n2 и n1 и по ним построены точки
n'2 и n'1 на проекциях a'b' u c'd'. Через n2' и n'1проведен след Pv до пересечения с осью х в точке Рх. Через точку Рх проведен след Рh параллельно прямой ab.
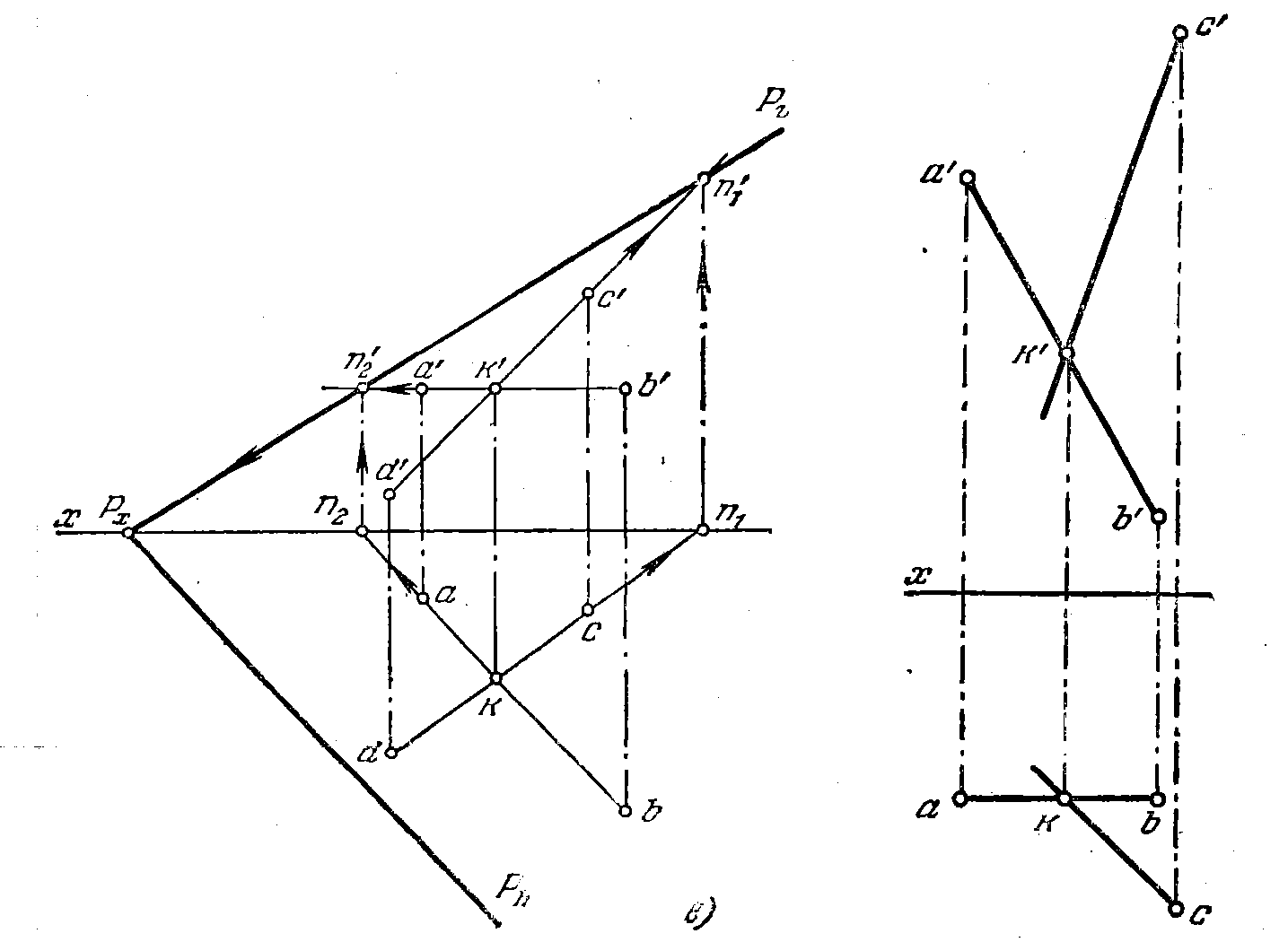
Рис. 52в: Рис. 53.
55. Построить следы плоскости, заданной пересекающимися пря-
прямыми АВ и КС (рис. 53).
56*. Построить недостающую проекцию отрезка АВ прямой, лежащей в плоскости Р (рис. 54, а). 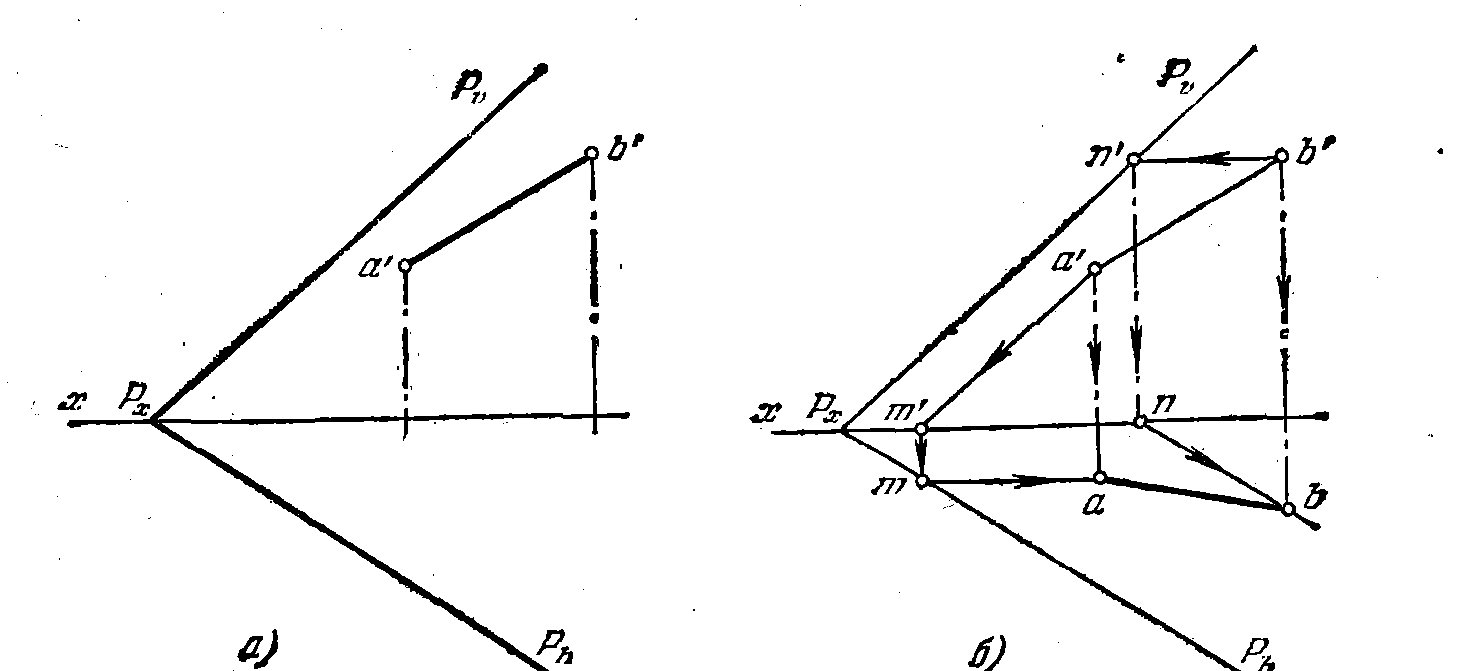
Рис.54 а,б.

Рис.55 а,б.
Решение. Чтобы построить горизонт, проекцию отрезка АВ, надо найти го-
горизонт, проекции точек А и В (рис. 54, б). Проекцию b находим с помощью
горизонтали, проведенной в плоскости. Сначала проводим проекцию Ь'n' параллельно оси х, затем через точку n — горизонт, проекцию горизонтали параллельно Рh и на ней находим проекцию b. Горизонт, проекцию точки А находим при помощи фронтали, хотя, конечно, можно было бы и для этой точки применить горизонталь. Через а' проводим фронт, проекцию фронтали (параллельно Pv), находим точки m' и m (проекции горизонт, следа фронтали ). Горизонт, проекция фронтали проходит через точку m
параллельно оси х; на этой проекции получаем точку а. Искомая проекция отрезка АВ определяется точками a и b,
а 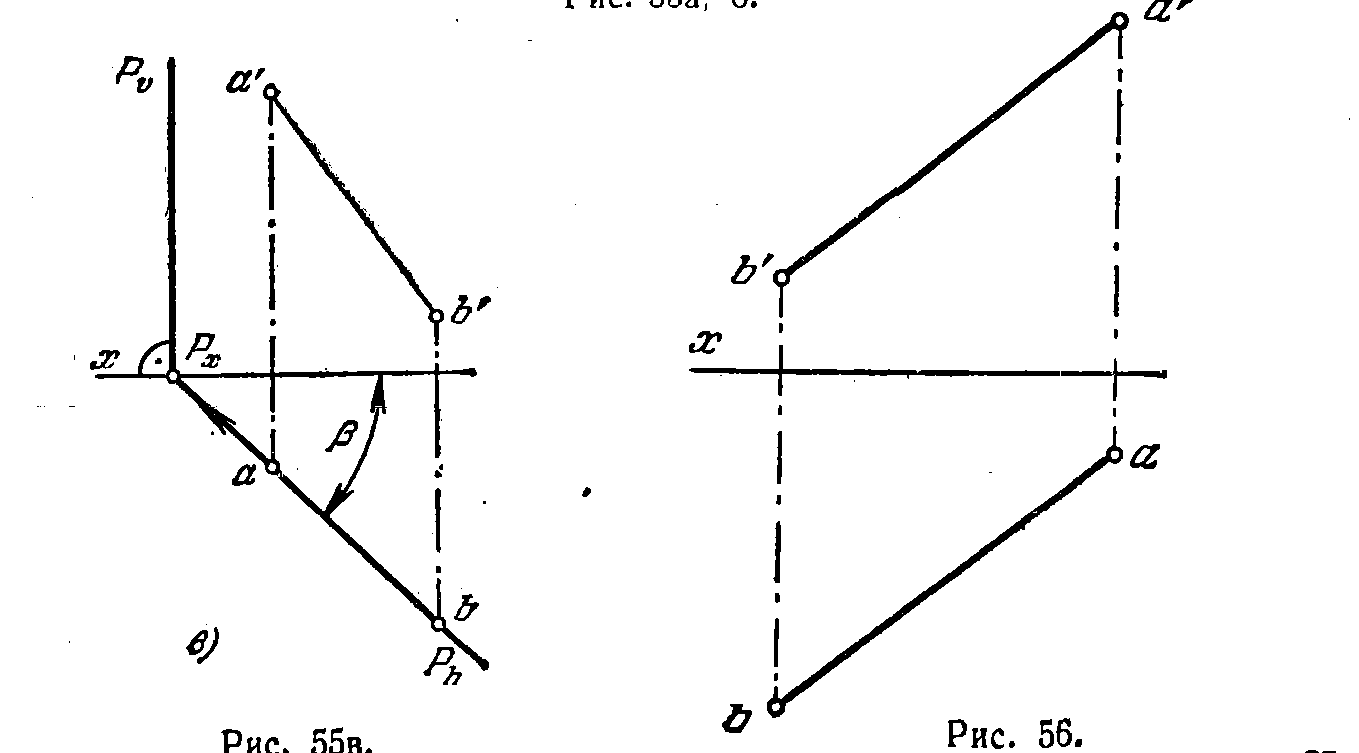
Рис. 55в . Рис. 56.
57*. Заключить прямую АВ (рис. 55, а) в горизонтально-проецирующую плоскость, задав эту плоскость ее следами на пл. И и V
Решение. Горизонтальные проекции всех элементов, лежащих в горизонтально-проецирующей плоскости, находятся на Ph. Поэтому (рис. 55, б) след Рн совпадает
с a b. Через точку Рх, получаемую при пересечении Ph с осью х, проводим перпендикулярно к оси х фронт, след искомой плоскости (Рv)
Угол между следом Ph и осью х равен углуb между пл. Р и пл. проекций V (рис.55, в).
58. Заключить прямую АВ (рис. 56) во фронтально-проецирующую плоскость, выразив эту плоскость следами на пл. V и Н. Построить чертеж и наглядное изображение. Указать угол наклона пл. Р к пл. Н.
59. Заключить прямую А В (рис. 57) в профильно-проецирующую
плоскость, выразив эту плоскость следами. Построить чертеж и дать
наглядное изображение. Указать углы наклона пл. Р к пл. V и Н.
Построение следов пл. Р выполнить с помощью профильной проекции прямой и без нее.
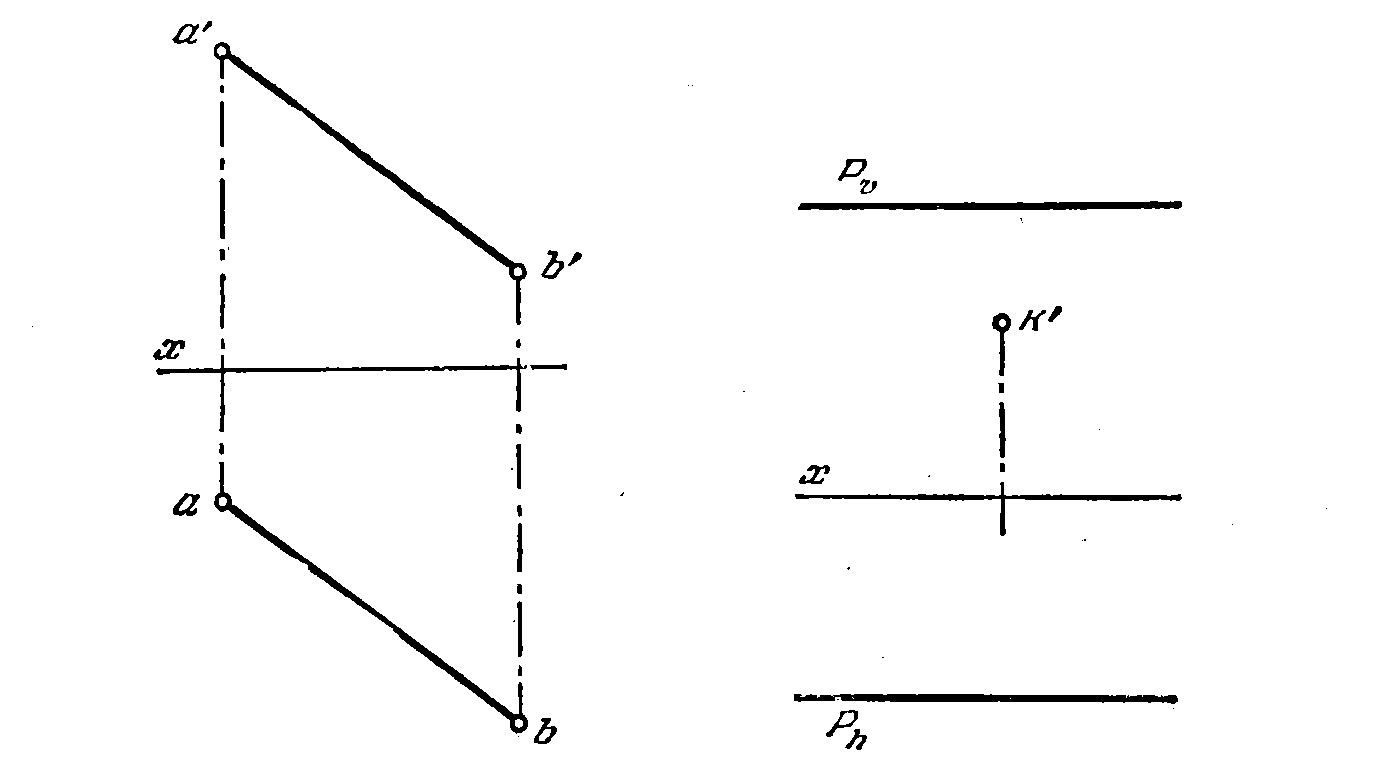
Рис. 57. Рис. 58
.
60. Построить недостающую проекцию точки К (рис. 58), лежащей в пл. Р (профильной плоскостью проекций не пользоваться.)
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПЛОСКОСТЬЮ
Дата добавления: 2018-02-18; просмотров: 3266; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!