Розв’язання задач по темі “Визначення переміщень у балках”.
Nbsp; Задача 7.5.Задано: Q=80 кН; h=12 см; h0=8 см; см; см; (рис.7.19). Побудувати епюру умовних дотичних напружень, перпендикулярних нейтральній осі (за формулою Журавського). Рис. 7.19 Розв’язання.Знаходимо значення дотичних напружень в точках 1 крайніх волокон перерізу, в точках 2 крайніх волокон порожнечі, в точках 3, найбільш віддалених від нейтральної осі на стінках порожнечі, і в точках 4 на нейтральній осі Z (рис.7.19). Для цього використаємо вираз для моменту інерції відносно нейтральної осі Z площі перерізу заданої форми см4. Для точок 1 S1=0; отже, і τ1=0. Для точок 2 см3 і МПа. Оскільки ширина перерізу в точках 3 дорівнює , то МПа. Для точок 4 см3, МПа.
Тема 8. Визначення переміщень у балках.
Лекція 16.Диференціальне рівняння зігнутої осі балки. Інтегрування диференціального рівняння зігнутої осі балки. Метод початкових параметрів.
1. Диференціальне рівняння зігнутої осі балки. Крім розрахунку на міцність, конструкції необхідно також розрахувати на жорсткість. При згині жорсткість характеризується здатністю балки чинити опір викривленню. Під дією зовнішніх навантажень, прикладених до балки, її первісно прямолінійна вісь викривляється. При деформації в межах пружності таку зігнуту вісь балки називають пружною лінією. Відхилення будь-якої точки пружної лінії балки від первісної прямої осі називають прогином y. Кут повороту будь-якого перерізу балки відносно його первісного положення (до деформації) називають кутом повороту перерізу q (рис.8.1).
|
|
|
Рис.8.1
Вище було встановлено, що кривизна пружної лінії прямо пропорційна величині згинаючого моменту
. (1)
При поперечному згині, крім переміщень, викликаних згинаючими моментами, виникають ще й переміщення, викликані поперечними силами.
Вплив поперечних сил на переміщення при згині залежить, в першу чергу, від відношення довжини прольоту балки l до її висоти h. Для балок з відношенням порядку 
впливом поперечних сил на величину прогинів можна нехтувати.
З курсу математики відомо, що
. (2)
Проте на практиці доводиться мати справу з малими прогинами балки, і диференціальне рівняння зігнутої осі балки можна спростити, нехтуючи величиною 
, як набагато меншою від одиниці.
Тоді одержимо наближене диференціальне рівняння зігнутої осі балки
. (3).
У випадку, коли вісь у напрямлена вгору, знаки кривизни і згинаючого моменту збігаються і у рівнянні (3) будемо брати знак “плюс”. Коли вісь у напрямлена вниз – у рівнянні (3) будемо брати знак “мінус”.
|
|
|
Згинаючий момент у рівнянні (3) слід підставляти із своїм знаком.
2. Інтегрування диференціального рівняння зігнутої осі балки. Наближене рівняння (3) зігнутої осі будемо інтегрувати для визначення переміщень при згині балки. Права частина цього рівняння містить вираз згинаючого моменту в довільному перерізі даної ділянки, а не в тому перерізі, для якого знаходять переміщення (прогини і кути повороту).
М(x) – величина змінна; тільки в випадку чистого згинуМ(x)=const.
Перший інтеграл диференціального рівняння (3) набирає вигляду
. (4)
Цей вираз визначає закон зміни кутів повороту в довільному перерізі балки.
Інтегруючи вдруге, знайдемо вираз для прогинів в довільному перерізі балки
. (5)
Для обчислення інтегралів спочатку треба написати аналітичні вирази для згинаючого моменту і жорсткості. Сталі величини С і D знаходимо за допомогою граничних умов.
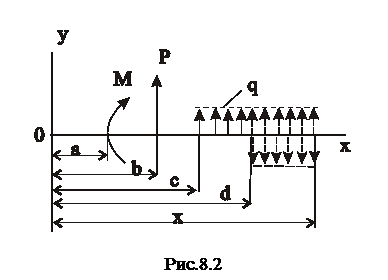3. Метод початкових параметрів. При визначенні деформації балок аналітичним методом зручно користуватися загальними (універсальними) рівняннями переміщень методу початкових параметрів.
|
|
|
Розглянемо одночасну дію навантажень на балку (рис.8.2).
Застосовуючи спосіб додаван- ня дії сил і диференціальні залежності, які існують для будь-якого перерізу балки між M, Q і q, одержимо так зване “універсальне” рівняння прогинів:
.
(6)
Диференціюючи рівняння прогинів, одержимо “універсальне” рівняння кутів повороту поперечних перерізів балки
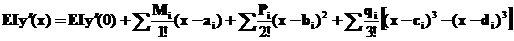. (7)
Початкові параметри y(0) і y¢(0) визначаються з умов на опорах балки.
Аналізуючи рівняння початкових параметрів (6) і (7), легко прийти до висновку, що вони побудовані таким чином, що для визначення зміщень зігнутої балки в будь-якому перерізі початок координат один і той самий, а члени рівняння, які з‘явились на тій чи іншій ділянці балки, діятимуть на всіх наступних ділянках. Причому, якщо розподілене навантаження на будь-якій ділянці закінчилося, на наступних ділянках з ростом величини хвідсутність навантаження треба скомпенсувати введенням фіктивного навантаження (вплив цього навантаження відображується останнім членом в “універсальних” рівняннях).
|
|
|
У рівняннях (6) і (7) слід враховувати тільки ті члени, які залежать від навантажень, розташованих між початком координат і розглядуваним перерізом бруса (балки).
Розв’язання задач по темі “Визначення переміщень у балках”.
Задача 8.1. Для консолі з прольотом ℓ, навантаженої в кінці зосередженою силою Р, треба визначити прогин і кут повороту поперечного перерізу кінця консолі (рис.8.1).
Рис. 8.1
Розв’язання.Виберемо за початок координат хуточку в опорному перерізі консолі. Згинаючий момент у довільному перерізі хдорівнює
.
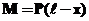Внаслідок малості переміщень вважаємо, що цей момент на залежить від прогинів. Підставивши значення М(х) у рівняння 
, матимемо
.
Інтегруючи перший раз , дістанемо
.
Тоді другий інтеграл набирає вигляду
.
Довільні сталі С1 і С2 визначаємо із граничних умов. В даному випадку при х=0 маємо у=0 і у′=0, звідки С1=0 і С2=0. Тоді одержимо: рівняння пружної лінії 
; рівняння кутів повороту
.
Найбільший прогин маємо у вільному кінці консолі при х=ℓ:
.
Кут повороту на вільному кінці балки буде таким:
.
Задача 8.2.Двохопорна балка довжиною ℓ, навантажена зосередженою силою Р на відстані а від лівої опори (рис.8.2). Треба скласти рівняння пружної лінії і знайти переміщення точки прикладення сили Р.
Розв’язання.В даному випадку згинаючі моменти на першій і другій ділянках балки мають такі вирази:
, 
.
Відповідно дістанемо два диференціальних рівняння пружної лінії:
, 
.
Інтегруючи кожне рівняння двічі, одержимо:
,
.
Сталі інтегрування визначаються із умов закріплення балки і умов неперервності при переході, з першої ділянки до другої, тобто
при х=0 у1=0
при х=а у1= у2 і у1′=у2′,
при х=ℓ у2=0.
Із цих умов знаходимо
,
.
Отже,
,
.
В точці прикладання сили Р
.
Якщо сила прикладена посередині прольоту балки, то
.
Координата в точці прикладання сили після згинання буде від’ємною, тому що прогин не збігається з віссю у.
Задача 8. 3.Написати рівняння пружної лінії для двохопорної балки (рис.8.3) і знайти переміщення точок прикладання сил.
Розв’язання.На лівій опорі балки реакція дорівнює нулю, на правій - 2Р. За початок координат вибираємо точку на лівій опорі. Отже, у0=0.
Рівняння пружної лінії балки в даному випадку має вигляд
.
Із умови у=0 при х=2ℓ визначаємо величину 
. Остаточно,
.
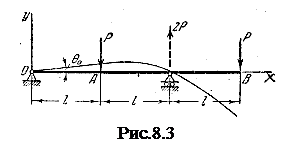Для визначення переміщення в точці А вибираємо тільки перший член рівняння і при х=ℓ знайдемо 
. Додатний знак вказує на те, що переміщення точки А збігається з напрямком осі у.
Для визначення переміщення точки Вприймаємо х=3ℓ і беремо всі члени рівняння. Тоді знаходимо
.
В даному випадку переміщення точки В не збігається з віссю у.
Задача 8.4.Підібрати двотавровий переріз балки (рис.8.4,а), якщо допустиме напруження для сталі [σ]=160 Мн/м2. Користуючись методом початкових параметрів, зобразити пружну лінію. Визначити кути повороту перерізів балки.
Розв’язання.
1. Визначення опорних реакцій.
; 
кН.
; 
кН.
Перевірка 
; 
.
2. Будуємо епюру згинаючих моментів. Максимальний згинаючий момент (рис.8.4,б):
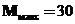кНм=0,03 Мн м.
3. Підбір перерізу. Визначаємо потрібний момент опору перерізу балки:
м3.
За сортаментом знаходимо двотавр:
№20 а: WZ=203 см3, IZ=2030 см4.
В подальшому позначено ІZ=I.
4. Вибираємо за початок координат лівий кінець балки (рис.8.4,в). Запишемо рівняння пружної лінії:
,
де навантаження беремо в меганьютонах, а відстань в метрах.
Визначимо початкові параметри у0і θ0, виходячи із умов на опорах: уА=0(при х=2); уВ=0 (при х=8).
Із першої умови уА=0 дістанемо рівняння:
.
Друга умова уВ=0дає
,
де 
М н/м2; 
м4.
Розв’язуючи сумісно ці два рівняння, одержуємо:
θ0=0,0019157 рад (0,09○);
у0= -0,00218937 м (-0,218937 см).
Визначимо прогин перерізу балки в середині прольоту (при х=5 м), підставивши в рівняння пружної лінії балки числові значення, при цьому навантаження при х>5 не враховується:
м = -1,67см
Знак “-“ показує, що переріз балки в середині прольоту зміщується вниз.
Для обчислення на ЕОМ рівняння пружної лінії зігнутої балки записуємо в такому вигляді:
,
де к=0,002189; ℓ=0,001915;
m=0,000102; n=0,000102;
p=0,001026; S=0,003694;
t=0,00820.
Продиференціюємо вираз у(х) по змінній х, дістанемо при цьому рівняння для кутів повороту:
.
Обчислимо значення прогинів і кутів повороту перерізів балки, беручи крок Δх=0,1 м.
Результати обчислення для прогинів показані в графічній формі (рис.8.4,в). Максимальне значення для кута повороту при х=8 м
рад.
Рис.8.4
Тема 9. Теорії міцності.
Лекція 17. Призначення теорій міцності. Теорія найбільших нормальних напружень (перша). Теорія найбільших лінійних деформацій (друга). Теорія найбільших дотичних напружень (третя). Енергетична теорія міцності. Теорія міцності Мора.
1. Призначення теорій міцності.Дуже важливим у курсі механіки твердого деформованого тіла є розділ, присвячений теоріям міцності. Насамперед треба добре ознайомитися з їх призначенням, чітко уявити, в яких випадках розрахунку на міцність доводиться звертатись до теорій міцності, вивчити основні теорії міцності і уміти записати умову міцності за кожною теорією для будь-якого складного напруженого стану.
Під небезпечним станом матеріалу розуміють: для крихких матеріалів – стан, при якому починається руйнування, а для пластичних матеріалів – стан, при якому виникають значні пластичні деформації. У випадку розтягу або стиску напруження, при яких виникає граничний стан (небезпечний стан) матеріалу, можуть бути визначені безпосередньо з випробування зразків матеріалу на розтяг або стиск. Експериментальне визначення граничних станів при складних напружених станах натрапляє на значні труднощі і не завжди можливе.
Щоб цього не робити, визначають за допомогою найпростіших випробувань (розтяг, стиск) механічні характеристики матеріалу і, знаючи їх, роблять висновки про поведінку матеріалу при інших навантаженнях на основі певних гіпотез, які прийнято називати “теоріями міцності”. Таким чином, завдання теорій міцності – виразити умови виникнення граничних напружених станів (поява пластичних деформацій або руйнування) матеріалу у будь-якому складному напруженому стані, коли відомі механічні характеристики матеріалу, одержані при його випробуванні в умовах лінійного напруженого стану.
2. Теорія найбільших нормальних напружень (перша).В основі теорії найбільших нормальних напружень лежить припущення, що причиною руйнування матеріалу є найбільші нормальні напруження. За цією теорією складний і лінійний напружений стани є рівнонебезпечними, якщо найбільші за абсолютною величиною головні напруження у них однакові. Для матеріалів, які не однаково чинять опір розтягу і стиску, умови міцності такі:
s1£[sp]; s3£[sс],
де 
– допустимі напруження, відповідно, при простому розтягу і стиску.
Перша теорія підтверджується дослідами над невеликою кількістю видів напруженого стану крихких матеріалів. Зараз вона майже не застосовується.
3. Теорія найбільших лінійних деформацій (друга).В основі теорії найбільших лінійних деформацій лежить припущення, що міцність матеріалу при будь-якому напруженому стані визначається величиною максимальних відносних деформацій. За цією теорією складний і простий напружені стани є рівнонебезпечними, якщо найбільші відносні лінійні деформації у них однакові.
Якщо при простому напруженому стані допустиме напруження дорівнює [σ], то умова міцності при складному напруженому стані за цією теорією виразиться рівністю
.
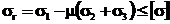Хоч теорія найбільших деформацій і враховує всі три головні напруження, для пластичних матеріалів вона не підтверджується дослідами. Для крихких матеріалів тільки при 
і 
, якщо при цьому 
(за абсолютною величиною), ця теорія узгоджується з даними дослідів.
4. Теорія найбільших дотичних напружень (третя).В основі теорії найбільших дотичних напружень лежить припущення, що причиною руйнування матеріалу є дотичні напруження. За цією теорією складний і простий напружені стани є рівнонебезпечними, якщо їх максимальні дотичні напруження дорівнюють одне одному. Тоді умова міцності при складному напруженому стані виразиться рівністю
sr= 
.
Ця теорія добре узгоджується з даними дослідів для пластичних матеріалів.
5. Енергетична теорія міцності. Як показують експериментальні дослідження, поява пластичних деформацій у ізотропних матеріалах зв‘язана з величиною питомої потенціальної енергії пружної деформації, витраченої на зміну форми тіла. Умова пластичності, виражена за допомогою такої енергії деформації, розглядається як енергетична теорія міцності.
Якщо при простому напруженому стані допустиме напруження матеріалу 
, то умову міцності при складному (об‘ємному) напруженому стані можна виразити рівністю
,
де sr – зведене (еквівалентне) напруження.
Енергетична теорія міцності добре узгоджується з даними дослідів для пластичних матеріалів і набула великого поширення в інженерній практиці при дослідженнях складного напруженого стану пластичних матеріалів.
6. Теорія міцності Мора.Вуглецеві сталі після гартування і невисокого відпуску, деякі бронзи та інші сплави мають при стиску більш високі границі пружності і текучості, ніж при розтягу. Внаслідок цього умови пластичності теорії найбільших дотичних напружень або енергетичної теорії зміни форми стають непридатними.
Вивчаючи теорію граничних напружених станів (теорію Мора), слід пам‘ятати, що аналітичний вираз цієї теорії
знайдено заміною справжньої граничної обвідної прямою лінією, дотичною до кругів допустимих напружень при простому стиску і розтягу. Для пластичних матеріалів допустимі напруження при розтягу 
і стиску 
однакові, і теорія Мора збігається з теорією найбільших дотичних напружень.
На практиці залежно від матеріалу застосовується та чи інша теорія міцності. Так, для пластичних матеріалів слід користуватися енергетичною теорією формозміни, або теорією найбільших дотичних напружень. Для крихких матеріалів (камінь, бетон, чавун та ін.), у яких граничні (допустимі) напруження на розтяг і стиск неоднакові, слід застосувати теорію Мора.
Розв’язання задач по темі “Теорії міцності”.
Задача 9.1. Для консольної балки (рис. 9.1,а), яка має довжину ℓ=2 м і з рівномірно розподілене навантаження інтенсивності q=20 кН/м, підібрати двотавровий переріз і провести перевірку балки за четвертою теорією міцності. Допустиме напруження для сталі [σ]=160 МПа.
Рис. 9.1
Розв’язання.Максимальний згинаючий момент і максимальна поперечна сила виникають в опорному перерізі балки: Мmax=40 кНм, Qmax=40 кН.
Визначимо момент опору
м3=250 см3.
Підбираємо двотавр №22 а (W=254 см3, А=32,8 см2, h=220 мм, в=120 мм, t=8,9 мм, d=5,4 мм, І=2790 см4. Епюри нормальних і дотичних напружень в поперечному перерізі балки показані схематично на рис.9.1.б,в. Небезпечними точками у перерізі є точки у місцях з’єднання полиці зі стінкою. Тут в епюрах (рис. 9.1.б,в) одночасно виникають близькі до максимальних нормальні 
і дотичні 
напруження. У даному випадку матеріал балки при поперечному згині перебуває у плоскому напруженому стані:
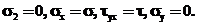
Умову міцності за енергетичною теорією міцності отримаємо, якщо підставимо у формулу 
значення головних напружень σ1 і σ3 :
.
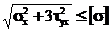Тоді 
.
Нормальні напруження в точках на переході від стінки до полички двотавра дорівнюють:
Па=141 МПа.
Дотичні напруження в точці з’єднання полиці зі стінкою двотавра визначаємо за формулою
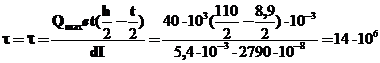Па=14 МПа.
За енергетичною теорією маємо
МПа.
Коефіцієнт запасу міцності в цьому випадку 
.
Задача 9.2.У стінці закритої чавунної труби від внутрішнього тиску виникають головні напруження: кільцеве σ1=20 МПа, осьове σ2=10 МПа і радіальне σ3=-0,8 МПа (рис.9.2). Границя міцності сірого чавуну на розтяг σв=160 МПа, коефіцієнт Пуассона μ=0,25. Треба визначити коефіцієнт запасу міцності.
Розв’язання.Чавун руйнується крихко. Застосуємо для перевірки міцності теорію найбільших нормальних напружень і теорію найбільших відносних подовжень. За першою теорією умова міцності виражається формулою
,
де 
,
звідки 
.
Приведене напруження за теорією відносних подовжень обчислюється за формулою 
і дорівнює 
МПа.
Отже, запас міцності дорівнює
.
Задача 9.3.Перевірити запас міцності стального вала, у якому при крученні виникають такі головні напруження: σ1=110 МПа, σ2=0, σ3= -110 МПа (рис.9.3). Матеріал Ст.45 з границею текучості σт=320 МПа.
Розв’язання.Оскільки матеріал конструкції пластичний, то для перевірки міцності треба використати теорію міцності найбільших дотичних напружень або енергетичну теорію зміни форми.
За теорією міцності найбільших дотичних напружень приведене напру-
ження обчислюється за формулою
і дорівнює 
МПа.
Коефіцієнт запасу міцності буде таким:
.
За енергетичною теорією міцності згідно виразу 
будемо мати 
МПа.
Тоді коефіцієнт запасу міцності в цьому випадку приймає значення
.
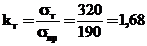Дата добавления: 2018-02-18; просмотров: 1807; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!