Тема 11. Енергетичні методи визначення переміщень при довільному
Навантаженні.
Лекція 19.Потенціальна енергія бруса у загальному випадку навантаження. Теорема Кастіліано. Інтеграл Мора.
1. Потенціальна енергія бруса у загальному випадку навантаження. В цій лекції слід показати, що у загальному випадку навантаження бруса (пружної системи) вираз для потенціальної енергії деформації набирає такого вигляду:
,
де U – потенціальна енергія деформацій пружної системи, Mk - крутячий момент, Mx, My - згинаючі моменти; N - нормальна сила, Qx, Qy - поперечні сили; Kx, Ky - коефіцієнти, які залежать від геометричної форми перерізу; GIk, EIx, EIy, EА, GА – жорсткості, відповідно: при крученні, згинанні, розтяганні (стисканні), зсуві.
Звернути увагу на те, що енергія розтягу і зсуву є значно меншою, ніж енергія кручення та згину.
2. Теорема Кастіліано. Для знаходження переміщень може бути використана теорема Кастіліано: переміщення точки прикладання сили в напрямі її дії дорівнює частинній похідній від потенціальної енергії деформації по цій силі.
Отже, 
, де Pn – узагальнена сила; dn - відповідне узагальнене переміщення.
Тоді прогин в точці прикладання зосередженої сили P1 обчислюється за такою формулою:
.
Для кута повороту перерізу, в якому діє момент пари, будемо мати такий вираз:
.
Слід сказати, що безпосередньо використовувати теорему не можна, якщо в перерізі відсутня узагальнена сила.
3. Інтеграл Мора. Здебільшого при визначенні переміщень у балках (рамах) можна знехтувати впливом поздовжніх деформацій і деформацій зсуву. Якщо позначити: 
, то переміщення можна знайти за допомогою формули Мора 
.
|
|
|
Слід підкреслити, що один із станів при застосуванні формули переміщень Мора повинен бути одиничний, тобто такий, в якому в місці і в напрямку шуканого переміщення прикладається одиничний силовий фактор.
При користуванні формулою Мора можна одержати переміщення з додатним або від‘ємним знаком. Додатний знак переміщення вказує на те, що його напрям збігається з прийнятим напрямом одиничного навантаження. При від‘ємному знаку дійсний напрям переміщення протилежний прийнятому для одиничної сили.
Слід показати декілька характерних прикладів визначення переміщень за формулою Мора.
Лекція 20.Визначення переміщень для прямих стержнів за правилом Верещагіна. Теорема про взаємність робіт та взаємність переміщень.
1. Визначення переміщень для прямих стержнів за правилом Верещагіна. Обчислення інтеграла Мора 
, який входить до формули переміщень, можна спростити, замінивши процес інтегрування так званим “перемноженням” епюр за правилом Верещагіна. Згідно з цим правилом, інтегрування замінюється геометричними операціями над епюрами Мі та Мк, побудованими для стану навантаження і та к. Зазначене правило діє лише при наявності в системі прямих брусків чи стержнів.
|
|
|
Правило Верещагіна виражається формулою
,
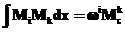тобто інтеграл Мора дорівнює добутку площі епюри від зовнішнього навантаження на ординату прямолінійної епюри від одиничного навантаження, взяту під центром ваги довільної епюри.
Інтеграл Мора можна також обчислити за правилом Симпсона-Корноухова
,
де MA і MB – кінцеві ординати епюр, Mc - ординати посередині бруса.
Визначені наведеними формулами ”перемноження” результати потрібно ще поділити на жорсткість бруса EI.
На лекції треба розглянути кілька простих прикладів застосування наведених правил знаходження переміщень.
2. Теорема про взаємність робіт та взаємність переміщень. Треба розглянути будь-яку пружну систему, яка навантажується статично прикладеними системами сил P1 та P2 в прямому та оберненому порядку. Оскільки початковий і кінцевий стани балки при обох порядках навантаження однакові, то будемо мати: A12=A21, що означає: робота сил першого стану навантаження на переміщеннях, викликаних силами другого стану, дорівнює роботі сил другого стану навантаження на переміщеннях, викликаних силами першого стану (теорема Бетті).
|
|
|
При рівних силах (P1=P2): d12=d21будемо мати теорему про взаємність переміщень (теорема Максвела).
Розв’язання задач по темі “Енергетичні методи визначення переміщень при довільному навантаженні.”
Задача 11.1.Визначити вертикальне переміщення точки А для конструкції, яка показана на рис.11.1. Жорсткості стержнів однакові і дорівнюють ЕА. При розв’язанні задачі використати теорему Кастіліано.
Розв’язання.Спочатку за допомогою методу вирізання вузлів знаходимо зусилля в кожному стержні. Отримані значення N наведено в таблиці.
Далі визначаємо потенціальну енергію для кожного стержня 
і заповнюємо останній стовпчик таблиці. Потім знаходимо суму 
. Тоді переміщення точки А буде дорівнювати
.
Таблиця
| Ni | 
| Uі | |
| 1 2 3 4 5 6 | Р
Р
-Р
2Р
| 
| 
|
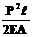
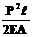
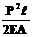
Задача 11.2.Для шарнірно обпертої балки, яка навантажена зосередженою силою Р (рис.11.2), визначити прогин Ус перерізу в точці прикладання сили Р і кут повороту θА в перерізі А. При визначенні переміщень беремо до уваги тілки вплив згинаючих моментів.
|
|
|
Рис.11.2
Розв’язання.Для визначення прогину Ус прикладаємо в його напрямі одиничну силу. Точка прикладання навантаження Р і одиничної сили розділяє балку на дві ділянки 0≤х1≤а, 0≤х2≤ 
.
На першій ділянці 
,
.
На другій ділянці 
,
.
Шуканий прогин
. Для знаходження кута повороту перерізу θА прикладаємо у його напрямі одиничну пару сил.
Тоді знаходимо на першій ділянці 0≤х1≤а
, 
;
на другій ділянці 0≤х2≤
, 
.
Шуканий кут повороту поперечного перерізу θА
.
Якщо 
, то 
, 
.
Задача 11.3.Визначити горизонтальне переміщення точки А бруса, зображеного на рис.11.3, беручи до уваги вплив лише згинаючих моментів. Жорсткість всіх ділянок є сталою і дорівнює ЕІ.
Розв’язання.Горизонтальне переміщення перерізу А бруса визначаємо за інтегралом Мора, який лише для згину запишеться так:
.
Згинаючий момент від сили Р на ділянці АВ дорівнює нулю. На ділянці ВС МР=Р·х, а на ділянці СD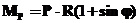 
. Момент від одиничної сили на ділянці АС дорівнює нулю, а на ділянці СD дорівнює
.
Цей вираз має знак “мінус” у зв’язку з тим, що одиничний згинаючий момент напрямлений в сторону, протилежну МР.
Добуток МР·М1 на ділянці АС буде дорівнювати нулеві. В зв’язку з цим інтегрування проводиться тільки на ділянці СD. Оскільки 
, будемо мати для горизонтального переміщення δА такий вираз:
,
звідки
.
Знак “мінус” вказує, що горизонтальне переміщення точки А не збігається з напрямком одиничної сили, а спрямовано в протилежний бік.
Задача 11.4.Визначити за формулою Мора прогин і кут повороту кінця консолі стальної балки (рис.11.4), приймаючи Р=20 кН, q=30 кН/м, ℓ=4 м, а=1м, І=3500 см4.
Розв’язання.Переміщення перерізу балки (прогин і кут повороту) за формулою Мора обчислюється так:
.
Тут М(х) або М – згинаючий момент у довільному перерізі балки згідно заданої схеми навантаження (рис.11.4,а), а М0 – згинаючий момент у тому ж перерізі від дії одиничного навантаження. При знаходженні прогину за одиничне навантаження приймаємо силу Р0=1, яку прикладаємо в перерізі, де шукаємо прогин (див.схему б)
Реакції в опорі В для відповідних схем будуть такі: 
, 
.
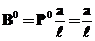На ділянці 0≤х1≤а маємо
; 
.
На ділянці 0≤х2≤ℓ маємо
; 
.
Тоді шуканий прогин буде таки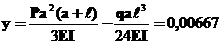м:
,
м.
Знак “мінус” вказує, що прогин спрямований в бік, протилежний напряму сили Р.
Рис.11.4
Для визначення кута повороту кінця консолі розглянемо ще один стан навантаження (схема в), коли на кінці консолі прикладається момент М0=1. Опорна реакція правої опори при цьому стані навантаження і одиничні згинаючі моменти відповідно будуть такими:
, 
, 
.
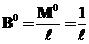Значення моментів М1 і М2 від заданого навантаження (схема а) обчислені попередньо. Тоді шуканий кут повороту обчислимо згідно виразу:
,
рад.
Задача 11.5.Визначити за методом Верещагіна кут повороту кінця лівої консолі стальної балки АВ, навантаженої, як показано на рисунку 11.5. Жорсткість балки дорівнює ЕІ=4∙1010 н∙см2, Р=10 кН, q=5 кН/м.
Розв’язання.Використаємо принцип незалежності дії сил і побудуємо окремо епюри згинаючих моментів: від сили Р (епюра б), від навантаження q в межах прольоту (епюра в), від навантаження q на консолі (епюра г).
Обчислимо площі цих епюр (від зовнішнього навантаження):
кн м2, 
кн м2,
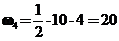кн м2, 
кн м2,
кн м2.
Для визначення кута повороту лівого кінцевого перерізу консолі балки прикладаємо у ньому одиничний момент М0=1 (схема д) і будуємо для нього епюру (схема е). Обчислимо значення ординат 
, які знаходяться проти центрів ваги площ, які показані на схемах б, в, і г. Ці ординати позначені відповідно на схемі е.
Отже, обчислимо величину шуканого кута повороту перерізу А:
кн м2.
рад.
Рис.11.5
Задача 11.6.Для консолі змінного поперечного перерізу з моментом інерції 
на ділянці 
та моментом інерції 
на ділянці ІІ, навантаженої зосередженою силою Р (рис.11.6), треба визначити, застосовуючи формулу Верещагіна, прогин і кут повороту кінцевого перерізу.
Розв’язання.Будь-яке переміщення ∆ для кількох ділянок навантаження балки обчислюємо за формулою Верещагіна так:
,
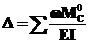де ω – площа епюри згинаючих моментів від заданого навантаження, а - ордината згинаючого моменту від одиничного навантаження (Р0=1 або М0=1), прикладеного в тому перерізі, де шукаємо переміщення. Ординату беремо відповідно в тому перерізі ділянки балки, напроти якої знаходиться центр ваги епюри згинаючого моменту від заданого навантаження на цій ділянці.
Спочатку будуємо епюру Мр для заданого навантаження (схема б). Далі визначаємо окремо площі ω1 і ω2 на кожній ділянці. Розбиваємо площу трапеції епюри Мр на ділянці І на два трикутники з площами ω1 і ω2. Площу трикутника на ділянці ІІ позначимо через ω3.
Для визначення прогину в точці прикладання сили Р прикладаємо в ній одиничну силу і будуємо епюру згинаючих моментів М1 (рис.11.6,в,г). Ординати цієї епюри, які розташовані проти центрів ваги площ ω1, ω2 і ω3, позначаємо відповідно через у1, у2, у3.
Тоді прогин кінця консолі
. Далі прикладаємо до кінцевого перерізу консолі одиничний момент і побудуємо для нього епюру М1 (рис.11.6, д, е). Тоді кут повороту кінцевого перерізу консолі буде мати таке значення:
.
Рис.11.6
Задача 11.7.Для плоскої рами (рис.11.7) треба визначити горизонтальне переміщення опори В від дії рівномірно розподіленого навантаження. Знайти також вертикальне переміщення перерізу С і кут повороту перерізу D. Жорсткість всіх трьох ділянок рами є однаковою.
Розв’язання.Для розв’язання задачі застосовуємо формулу Верещагіна. Спочатку від заданого навантаження (схема а) побудуємо епюри згинаючих моментів (схема б). Покажемо положення центрів ваги площ і обчислимо величину площі кожної ділянки епюр:
, 
.
Далі для визначення горизонтального переміщення опори В прикладаємо до рами горизонтальну одиничну силу Р0=1 (схема в). Побудуємо від цього одиничного навантаження епюри згинаючих моментів (схема г) і позначимо на кожній ділянці цих епюр відповідні ординати, які розташовані відповідно під центрами ваги площі кожної ділянки епюри від заданого навантаження:
, 
.
Тоді горизонтальне переміщення опори В рами будемо визначати так:
.
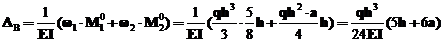Для визначення вертикального переміщення перерізу С потрібно прикласти в цьому перерізі рами силу Р0=1, яка діє вертикально, і для цього стану навантаження побудувати епюру згинаючого моменту, а потім обчислити ординати цієї епюри, що відповідають положенням центрів ваги від заданого навантаження (схема б). В подальшому знову треба виконати дії по перемноженню площ епюр від заданого навантаження на обчислені, як вказано вище, ординати епюр від одиничного навантаження. Взявши суму цих добутків і розділивши на жорсткість, отримаємо величину вертикального переміщення перерізу С.
Для визначення кута повороту перерізу D треба розглянути стан навантаження рами моментом М0=1, який прикладаємо в перерізі, де потрібно визначити кут повороту. Потім знову виконуємо дії згідно методики, яка є аналогічною.
Відповідь: 
; 
.
Рис.11.7
Дата добавления: 2018-02-18; просмотров: 1656; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!