Телеграфный сигнал как частный случай случайного процесса.????
Наиболее распространенными моделями случайных сигналов и помех являются телеграфный сигнал, белый шум, гауссовский случайный процесс, гауссовский шум.
Телеграфный сигнал- это случайный процесс xk(t), представляющий собой последовательность прямоугольных положительных и отрицательных импульсов со случайными длительностями и детерминированными значениями амплитуд c и -с, причем перемены знака внутри любого интервала (t, t+τ) происходят с интенсивностью в случайные моменты времени и не зависят от процессов в смежных временных интервалах. Если считать случайной величиной телеграфного сигнала значение n - количество перемен знака внутри интервала то распределение вероятностей значений n будет описываться законом Пуассона:
P(n) = (α|τ|)2 exp(-α|τ|)/n! (17.4.1)
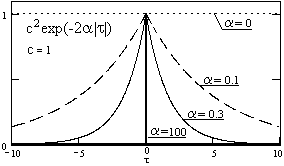При вычислении корреляционной функции телеграфного сигнала каждое отдельное произведение xk(t)xk(t+τ) равно либо с2, либо -с2 в зависимости от совпадения или несовпадения знаков xk(t) и xk(t+τ), причем вероятность с2 равна сумме вероятностей Р(0)+Р(2)+Р(4)+..., а вероятность -с2 определяется соответственно суммой вероятностей Р(1)+Р(3)+Р(5)+... .
Следовательно:
Rx(τ) = c2 exp(-α|τ|) 
(-1)n(α|τ|)n/n! = c2 exp(-2α|τ|). (17.4.2)
Параметр α полностью определяет ковариационные и спектральные свойства телеграфного сигнала. При α->0 характеристики сигнала приближаются к характеристикам постоянной составляющей, при α-> 
к характеристикам белого шума.
|
|
|
Интервал ковариации сигнала: Tk=2 
(Rx(t)/c2)dt=2/a.
Отсюда следует, что чем больше a, тем меньше время ковариации процесса. При a Þ 0 Tk Þ ¥ и процесс вырождается в детерминированный (стремится к постоянной составляющей). При a Þ ¥ Tk Þ 0 и процесс вырождается в белый шум с некоррелированными отсчетами даже на соседних временных точках.
Двусторонняя спектральная плотность сигнала:
Sx(w)= 
Rx(t) exp(-jwt) dt= ac2/(a2+w2). (9.4.4)
Односторонняя спектральная плотность:
Gx(w)= 2ac2/(a2+w2). (9.4.5)
Ширина спектра телеграфного сигнала:
Bk = Gx(w) dw/Gx(0) º Sx(w) dw/Sx(0) = ap. (9.4.6)
Отсюда следует, что спектр случайного процесса тем шире, чем меньше интервал ковариации процесса.
Коды Хемминга.
Одним из первых корректирующих кодов был предложен код Р. Хемминга. Он основан на простейшей идее: синдром ошибки является двоичным кодом номера разряда с ошибкой. Например, код синдрома 101 должен соответствовать пятому разряду с ошибкой.
Для того, чтобы это правило срабатывало, необходимо составить таблицу соответствия, в которой синдром должен однозначно определять номер разряда с ошибкой. Приведем пример для 8-разрядного кода. В этом коде (7.4) ( 
– общее число разрядов; 
– количество информационных разрядов) можно представить таблицу соответствия:
|
|
|
Рис. 6.28. Матричное и алгебраическое представление кода Хемминга
Справа приведена система проверочных равенств, которая реализована по следующему принципу: по каждому столбцу двоичных кодов синдромов приводятся соответствующие разряды, которые суммируются по модулю 2 и приравниваются к 0. Рассмотрим последние разряды таблицы синдромов. Разряду с единицами соответствуют 
, 
, 
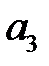и 
. Из этого вытекает первое проверочное равенство: 
. Аналогично реализуются и другие проверочные равенства.
Предположим, 
. Вычислим необходимое число контрольных разрядов: 
. Путем подбора получаем 
. Тогда 
.
Составляем таблицу синдромов и примыкающую к ней систему проверочных равенств (рис. 6.29).
Рис. 6.29. Матричное и алгебраическое представление кода Хемминга (13,9)
Из выражений по рис 6.28 и 6.29 можно интерпретировать код Хемминга на любое количество разрядов.
Из приведенных выражений непонятно, как назначать контрольные разряды. В принципе, они могут быть любыми. Желательно, однако, чтобы количество вычислений при кодировании и декодировании было минимальным. Для этого желательно выполнить критерий минимальной разрешимости, согласно которому из системы проверочных равенств нужно выбрать такие контрольные разряды, при которых системы уравнений становятся вырожденными. Это происходит, когда каждый член системы уравнений присутствует в ней однократно. Тогда система уравнений по рис. 6.29 преобразуется к виду:
|
|
|
| (6.30) |
В алгебре сложения по модулю 2 достаточно перенести любое количество слагаемых из одной части уравнения в другую; результат при этом не меняется.
Аналогично для второй системы проверочных равенств по рис. 6.30 получаем:
| (6.31) |
Из приведенных соотношений (6.30) и (6.31) вытекает следующее:
1. контрольные разряды должны соответствовать степени двойки. Таким образом, номера контрольных разрядов в дальнейшем равны а16, а32,…,а2к.
2. при той же корректирующей способности увеличение общего количества разрядов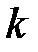 
приводит к положительному эффекту.
Обратимся к определению скорости кода:
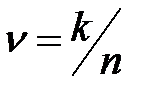
| (6.32) |
Преобразуем выражение (6.32) к виду:
| (6.33) |
При этом в связи с увеличением 
скорость повышается с увеличением 
.
|
|
|
Контроль на четность может быть реализован как на программном, так и на аппаратном уровнях. В последнем случае структура передающей части принимает вид, приведенный на рисунке 6.31.
Рис. 6.30. Контроль на четность
Здесь элемент D1 – счетный триггер, переходящий в противоположное состояние при каждом импульсе на входе. После прохождения всего кода при четном количестве единиц на последнем разряде будет присутствовать ноль, в противном случае – единица.
Для формирования кода Хемминга в общем случае необходимы более сложные процедуры. Рассмотрим код (7,4). В реализации кода (7,4) на передающей части необходимо реализовать уравнения (6.30). Они представляются в виде структурной схемы (рис. 6.31).
Здесь схемы совпадения D1,…, D4 выделяют информационные разряды, причем разряды «подаются » задом наперед. Схема D5 объединяет информационные разряды в нужные такты. Так, первое уравнение системы (3.30) реализуется схемой D6 и D9, причем счетный триггер D9 реализует контроль на четность. Предварительно триггер D9 устанавливается в 0. Аналогично работают остальные устройства. Так, схема D7 организует второе проверочное равенство из системы (6.30).
Рис. 6.31. Структура кодера Хемминга
Декодирующая система, реализующая алгоритм (6.31), может представиться в виде, представленном на рисунке 6.33.
Здесь верхняя часть схемы представляет систему приема и коррекции кода. Схемы D1,…, D4 выделяют информационные разряды, которые заносятся в буферную память на счетных триггерах D5,.., D8.
Нижняя часть устройства организует контроль на четность. Для этого на схемах D13, D14, D15 выделяются нужные такты для проверочных равенств по рисунку 3.30. Например, схема «ИЛИ» D13 формирует первое равенство ( 
).
Схемы D16, D17, D18 выделяют единицы из принятого кода в соответствии с проверочными равенствами, а счетные триггеры D19, D20, D21 проводят контроль на четность.
В соответствии со свойствами кодов Хемминга двоичный код синдрома преобразуется в позиционный с помощью дешифратора D22. Восьмым тактом на схемах D23,…, D26 выделяется импульс коррекции (один из возможных импульсов) при наличии одиночной ошибки. Импульс коррекции поступает на С – вход соответствующего триггера D5,…, D8. В этот же такт осуществляется считывание скорректированного кода через схемы D9,…, D12.
Как видно из приведенных схем, кодирование и декодирование последовательных кодов достаточно громоздко.
Рис. 6.32. Дешифратор кода Хемминга (7,4)
Приведем примеры кодирования и декодирования в алгебраической форме. Предположим, безызбыточный код иметь вид 1011. Эти разряды соответствуют позициям кода , , 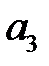и . соответственно. Вычислим контрольные разряды в соответствии с проверочными равенствами:
|
Окончательно код принимает вид 0110011. Аналогично вычисляются остальные коды при 15 возможных комбинациях безызбыточного кода.
Займемся теперь приемом, причем за базу примем сформированный код. Предположим, код принят без ошибок. Тогда при приеме формируется следующий синдром:
То есть, ошибки не обнаружены. Представим теперь, что произошла ошибка в разряде , т. е. код имеет вид 0110111. Вычисляем синдром:
Получим синдром, соответствующий десятичной цифре 5 – ошибка в пятом разряде исправляется.
Теперь представим, что произошла двойная ошибка, и кол принимает вид 1110111. синдром получается следующего вида:
Синдром вида 110 означает ошибку в разряде; после её исправления в коде будет уже не две, а три ошибки. Этот эффект носит название размножения ошибок и является большим недостатком корректирующих кодов: если количество ошибок превышает допустимое, при декодировании ошибки размножаются.
Коды Хемминга относятся к числу академических: они в принципе реализуемы, но неэффективны. Можно повысить их корректирующую способность, но не намного и неэффективно. В частности, существует способ повышения кодового расстояния от 
(классический код Хемминга) до 
. Для этого вводится дополнительный контрольный разряд с контролем на четность. В частности, для кодов Хемминга (7,4) вводится дополнительный 8-й разряд, который для передающей части записывается в виде:
 ,
| (6.34) |
а для приемной:
 .
| (6.35) |
Полученный код интерпретируется достаточно просто. Он способен исправлять одиночные ошибки и обнаруживать двойные. Правило достаточно простое: если при приеме появился ненулевой синдром, а в дополнительном разряде 0, это признак двойной ошибки, и принятый код отбрасывается.
Дата добавления: 2018-02-18; просмотров: 1473; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!