Эргодические случайные процессы. Необходимое и достаточное условие эргодичности.
Эргодическими называют такие случайные процессы, для которых усреднение по ансамблю реализации можно заменить усреднением по времени. Практически это означает, что можно исследовать один объект вместо 
однотипных объектов (что нереально). По одному объекту можно делать статистические обобщения на аналогичные технические объекты. Примеров можно привести достаточно много: баллистическая ракета, корабль, подводная лодка, самолет, электровоз, вагон, нефтеперегонная установка и т.д. Для исследования берут одни объект из серии однотипных и проводят на нем эксперименты.
С позиции теории вероятностей производятся следующие эквивалентные вычисления. Математическое ожидание заменяется средним по времени значением:
| (4.53) |
Здесь 
– интервал реализации, время, на котором происходит вычисление. В дискретной форме это выражение принимает вид:
| (4.54) |
Аналогичные выражения возможны и для других рассмотренных выше количественных оценок. В частности, для дисперсии интегральная и суммарная оценки принимают вид:
| (4.55) |
Аналогичные выражения существуют и для корреляционной функции:
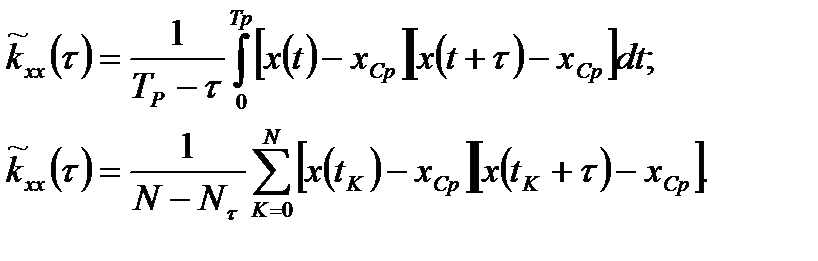
| (4.56) |
Выражения (4.56) нуждаются в интерпретации. Появляется множитель 
, что приводит к неустойчивости вычислений при 
(любое случайное отклонение приводит к серьезным отклонениям от желаемого результата). Поэтому корреляционную функцию обычно вычисляют при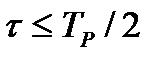 
. Проиллюстрируем сказанное графиком, приведенным на рис.4.21. Из графика видно, что корреляционная функция не затухает, что свидетельствует об отсутствии эргодичности. С позиции математики должны быть необходимое и достаточное свойства.
|
|
|
Рис. 4.21. Интерпретация задачи эргодичности
Необходимое условие: для того, чтобы процесс был эргодическим, необходимо, чтобы он был стационарным, т. е. должны выполняться условия:
| (4.57) |
Достаточное условие формулируется в следующей форме:
| (4.58) |
Это наиболее уязвимое свойство эргодичности, так как в соответствии с рисунком 4.21 абсолютное затухание корреляционной функции трудно доказать экспериментально. Более «мягкое» решение можно получить при следующем ограничении:
| (4.59) |
Количественные оценки эргодических случайных процессов.
Количество информации: определение и свойства.
На основании введённых понятий можно ввести определение количества информации. Обратимся к простейшей модели передачи информации, изображённой на рис. 1.16.
Рис. 1.16. Модель передачи информации
В ней источник вырабатывает сообщения 
, а приёмник по ним восстанавливает символы 
(в общем случае 
). При передаче одного символа неопределенность источника снижается на величину
|
|
|
 ,
| (1.99) |
где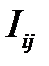 
– количество информации, полученное при приёме 
.
Просуммируем все возможные состояния с учетом их вероятностей:
 .
| (1.100) |
Применим формулу Байеса:
 .
| (1.101) |
Второй член в (1.101), в соответствии с (1.95), равен условной энтропии 
. Поскольку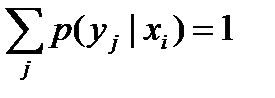 
, окончательно из (1.101)
 .
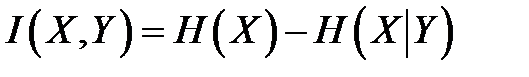| (1.102) |
Поскольку формулу Байеса можно написать в симметричной форме, получим формулу:
 ,
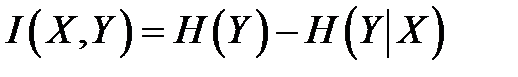| (1.103) |
Теперь, выразив из (1.96) условную энтропию и подставив в (1.103), получаем:
 .
| (1.104) |
Отметим, прежде всего, что и энтропию источника (выражение (1.89)), и полную энтропию (1.91), и количество информации (1.100) можно трактовать как математическое ожидание, приходящееся на один символ. В первом случае это среднее значение частной энтропии 
, во втором – частной совместной энтропии – 
, в третьем – частного количества информации 
.
Второе, не менее важное свойство количества информации – симметричность передачи информации. Выражение (1.102) задает количество информации относительно источника, (1.103) относительно приёмника, а (1.104) относительно всего информационного канала. Вследствие этого количество информации – величина скалярная. Кроме этого, указанное свойство требует учитывать свойства всего канала целиком. Например, источник может увеличить скорость передачи сообщений, но если она недопустима для линии связи (ограничение частотного диапазона) или приёмника (ограничение скорости декодирования), количество информации на символ даже уменьшится, поскольку не все символы сообщения восстановятся приёмником.
|
|
|
Сделаем количественную оценку 
.
1. 
. Это вытекает из соотношений (1.102) и (1.97).
2. Количество информации минимально, если 
и 
никак не связаны. В этом случае 
и из (1.102) 
. Это свойство легко интерпретируется практически: если вам что-то говорят на незнакомом вам языке, информацию вы не получаете.
3. Информация максимальна, если 
: 
. Это позволяет определить энтропию источника как максимальное количество информации, которое можно от него получить. В свою очередь, из свойств 2 и 3 условная энтропия приобретает смысл потерь информации.
Определим теперь количество информации непрерывных сообщений. Пример источника непрерывных сообщений – объект, один из параметров которого нужно измерить (например, температуру, давление, скорость и т.д.). На первый взгляд может показаться, что такие источники могут иметь бесконечную энтропию даже в ограниченном диапазоне. Фактически любая процедура получения информации от такого источника (она называется измерением) имеет погрешность. Погрешность вызывается неточностью измерителя и флуктуациями самого параметра. Примем, что в диапазоне изменения величины 
измерение происходит с абсолютной погрешностью 
. Тогда мы условно можем выделить 
дискретных состояний с шагом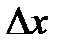 
(или квантов), а энтропия при условии равновероятных состояний
|
|
|
 .
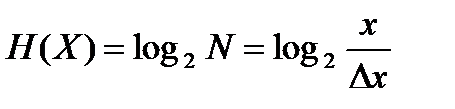| (1.105) |
Эта формула аналогична энтропии по Хартли (1.90). Из неё видно, что увеличение точности измерения (снижение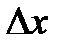 
) повышает количество информации от источника.
Более точное выражение для количества информации с учетом распределения вероятности величины 
определено К. Шенноном. Если предположить, что 
– измеряемый физический параметр, а 
– результат измерения, то количество информации в одном измерении:
 .
| (1.106) |
Здесь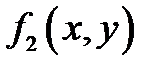 
– двумерная плотность распределения. Применим формулу Байеса:
 ,
| (1.107) |
где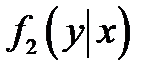 
– условная плотность распределения. Подставим (1.107) в (1.106):
Поскольку 
(условие нормировки), получим
  .
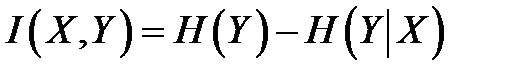| (1.108) |
Получили выражение, тождественное (1.103) для дискретных сигналов, только в нём энтропии вычисляются по-другому:
 ;
| (1.109) |
 .
| (1.110) |
Аналогично запишутся выражения для 
и 
:
 ;
| (1.111) |
 .
| (1.112) |
Дата добавления: 2018-02-18; просмотров: 1901; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!