ЗАСТОСУВАННЯ СТЕПЕНЕВИХ РЯДІВ ДО НАБЛИЖЕНИХ ОБЧИСЛЕНЬ, ІНТЕГРУВАННЯ ДЕЯКИХ ФУНКЦІЙ І РОЗВ’ЯЗАННЯ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ
Зауважимо, що у цьому розділі корисно мати на увазі формули для розкладу у степеневі ряди функцій

Для обчислення логарифмів корисна формула

Ряд у правій частині цієї рівності швидко збігається.
Для обчислення наближеного значення функції  у її розкладі у степеневий ряд залишаються перші
у її розкладі у степеневий ряд залишаються перші  членів (
членів (  - кінцева величина), а інші відкидаються. Для оцінки погрішності знайденого наближеного значення треба оцінити суму відкинутих членів. Якщо даний ряд знакопостійний, то ряд, зіставлений з відкинутих членів, порівнюють із нескінченною спадною геометричною прогресією. У випадку знакозмінного ряду, члени якого задовольняють ознаці Лейбніца, використовується оцінка
- кінцева величина), а інші відкидаються. Для оцінки погрішності знайденого наближеного значення треба оцінити суму відкинутих членів. Якщо даний ряд знакопостійний, то ряд, зіставлений з відкинутих членів, порівнюють із нескінченною спадною геометричною прогресією. У випадку знакозмінного ряду, члени якого задовольняють ознаці Лейбніца, використовується оцінка  , де
, де  - перший з відкинутих членів.
- перший з відкинутих членів.
Приклади.1. Використовуючи розклад у ряд функції 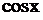 , обчислити
, обчислити 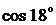 з точністю 0,0001.
з точністю 0,0001.
20
Розв’язок.


Достатньо взяти три члени ряду, тому що  Отже
Отже

2. Обчислити  із точністю до 0,001.
із точністю до 0,001.
Розв’язок. Тому що 53 є найближчий до числа 130 куб цілого числа, то доцільно число 130 представити у вигляді суми : 130 = 53 +5. 
Четвертий член менший за 0,001, тому його та слідуючі за ним члени можна відкинути. Отже, 
3. Обчислити ln1,04 з точністю до 0,0001.
Розв’язок. Скористаємось розкладом 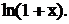


4. Обчислити з точністю до 0,0001 визначений інтеграл 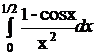 .
.
Розв’язок. Замінимо у підінтегральному виразі  його розкладом у степеневий ряд
його розкладом у степеневий ряд
21
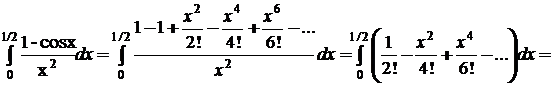
|
|
|
= 
Таким чином,
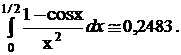
5. Обчислити з точністю 0,001 визначений інтеграл 
Розв’язок.

 .
. 
 0 098.
0 098.
Розглянемо застосування степеневих рядів для розв’язування диференціальних рівнянь.
У деяких випадках, коли інтегрування диференціальних рівнянь у елементарних функціях неможливо, можна шукати розв’язок такого рівняння у вигляді степеневого ряду

Невизначені коефіцієнти Сn (n =0, 1, 2, …) знаходяться за допомогою підстановки цього ряду у дане рівняння і прирівнювання коефіцієнтів при однакових ступенях різниці х – х0 у обох частинах одержаної рівності. Якщо удається визначити усі коефіцієнти, то одержаний ряд визначає розв’язок в усій області своєї збіжності.
У тих випадках, коли для рівняння  треба розв’язати задачу Коші при початкових умовах
треба розв’язати задачу Коші при початкових умовах  розв’язок можна шукати за
розв’язок можна шукати за
22
допомогою ряду Тейлора:
 де
де  а інші похідні
а інші похідні  знаходяться послідовним диференціюванням даного рівняння і підстановкою замість
знаходяться послідовним диференціюванням даного рівняння і підстановкою замість  і т.п. -
і т.п. -  і значень інших знайдених похідних. Аналогічно за допомогою ряду Тейлора можна інтегрувати і рівняння вищих порядків.
і значень інших знайдених похідних. Аналогічно за допомогою ряду Тейлора можна інтегрувати і рівняння вищих порядків.
|
|
|
Приклади.
1. 
 = 0.
= 0.
Розв’язок. Будемо шукати розв’язок цього рівняння у вигляді ряду
 . Підставляємо цей ряд і його другу похідну у дане рівняння:
. Підставляємо цей ряд і його другу похідну у дане рівняння:



Зберемо члени з однаковими ступенями х:
2 
Прирівнюючи нулю усі коефіцієнти одержаного ряду (щоб рівняння перетворилось у тотожність), маємо:

Останнє співвідношення дозволяє найти послідовно коефіцієнти шуканого розкладу (С0 і С1 залишаються довільними і грають роль довільних сталих інтегрування):
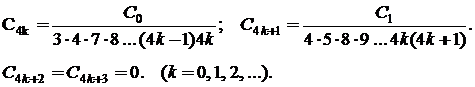
Таким чином, знаходимо:
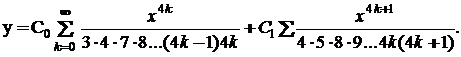
Одержані ряди збігаються на усій числовій осі і визначають два лінійно
незалежних частинних розв’язки даного рівняння.
23
2. Знайти шість перших, не рівних нулю, членів розкладу у ряд Тейлора розв’язку рівняння 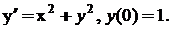
Розв’язок. Із даного рівняння і початкової умови одержуємо:

Диференціюючи дане рівняння, знаходимо послідовно:

Підставляючи х = 0 і використовуючи значення  знаходимо послідовно:
знаходимо послідовно:
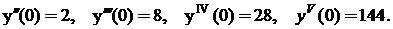
Таким чином, шуканий розв’язок має вигляд:


3. 
Знайти перші чотири (відмінних від нуля) члени розкладу .
Розв’язок. Диференціюючи дане рівняння, маємо:

При х = 0 одержуємо:

Отже


|
|
|
24
Дата добавления: 2018-02-15; просмотров: 2606; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
