РЯДИ З ДОДАТНИМИ ЧЛЕНАМИ. ОЗНАКИ ПОРІВНЯННЯ . ОЗНАКИ ДАЛАМБЕРА І КОШІ. ІНТЕГРАЛЬНА ОЗНАКА КОШІ-МАКЛОРЕНА
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНА МЕТАЛУРГІЙНА АКАДЕМІЯ УКРАЇНИ

МЕТОДИЧНІ ВКАЗІВКИ
До вивчення дисципліни «Вища математика»
(розділ «Числові та степеневі ряди»)
Для студентів усіх спеціальностей
Дніпропетровськ НМетАУ 2009
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНА МЕТАЛУРГІЙНА АКАДЕМІЯ УКРАЇНИ
МЕТОДИЧНІ ВКАЗІВКИ
До вивчення дисципліни «Вища математика»
(розділ «Числові та степеневі ряди»)
Для студентів усіх спеціальностей
ЗАТВЕРДЖЕНО
на засіданні Вченої ради
академії
Протокол № 9 від 30.12.08
Дніпропетровськ НМетАУ 2009
УДК 517.3
Методичні вказівки до вивчення дисципліни «Вища математика» ( розділ «Числові та степеневі ряди ») для студентів усіх спеціальностей / Укл.:
В. С. Коноваленков, Т. М. Заборова. – Дніпропетровськ: НМетАУ, 2009. – 48с.
Містять відомості про дослідження числових та степеневих рядів. Дано основні визначення, ознаки збіжності для знакопостійних та знакозмінних числових рядів.
Розглянуті степеневі ряди та методи знаходження інтервалів їх збіжності або розбіжності, а також приклади застосування рядів для інтегрування функцій, розв’язання диференціальних рівнянь, наближених обчислень. Крім того, наведені варіанти завдань для індивідуальної роботи.
|
|
|
Призначені для студентів усіх спеціальностей
Друкується за авторською редакцією
Укладачі: В. С. Коноваленков, канд. техн. наук, доц.
Т. М. Заборова, ст. викладач
Відповідальний за випуск Г. Г. Швачич, канд. техн. наук, проф.
Рецензент Ю.Н. Головко, канд. фіз.-мат.наук, доц. ( НГУ)
Підписано до друку 07.05.09. Формат 60х84 1/16. Папір друк. Друк плоский.
Облік.-вид. арк. 2,82. Умов. друк. арк.2,78. Тираж 100 пр. Замовлення №
Національна металургійна академія України
49600, м. Дніпропетровськ-5, пр. Гагаріна, 4
_______________________________
Редакційно-видавничий відділ НМетАУ
ЗМІСТ
1. Числова послідовність. Числові ряди. Збіжність ряду, його сума.
Необхідна умова збіжності. Властивості збіжних рядів….………………….4
2. Ряди з додатними членами. Ознаки порівняння. Ознаки Даламбера і
Коші. Інтегральна ознака Коші-Маклорена…………………………………..7
|
|
|
3. Знакозмінні ряди. Абсолютна та умовна збіжність ряду.
Ознака Лейбніца. Теоретичні відомості……………………………………...10
4. Функціональні ряди. Степеневі ряди…………...........................................12
5. Ряди Тейлора і Маклорена………………………………………………....17
6. Застосування степеневих рядів до наближених обчислень,
інтегрування деяких функцій і розв’язання диференціальних рівнянь……20
7. ВАРІАНТИ ЗАВДАНЬ ДЛЯ КОНТРОЛЬНИХ РОБОТ…………………...25
ЛІТЕРАТУРА……………………………………………………………………48
3
ЧИСЛОВА ПОСЛІДОВНІСТЬ. ЧИСЛОВІ РЯДИ. ЗБІЖНІСТЬ РЯДУ, ЙОГО СУМА. НЕОБХІДНА УМОВА ЗБІЖНОСТІ. ВЛАСТИВОСТІ ЗБІЖНИХ РЯДІВ
Розглянемо числову послідовність 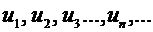 , де
, де 
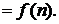
Побудуємо із цієї послідовності вираз 
Цей вираз називається нескінченим числовим рядом, а член  його загальним членом. Числовий ряд часто записують у вигляді
його загальним членом. Числовий ряд часто записують у вигляді 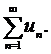
Суму n членів числового ряду позначають  і називають n - ю
і називають n - ю
частинною сумою ряду:

Ряд  називається збіжним, якщо його n – а частинна сума
називається збіжним, якщо його n – а частинна сума  при нескінченому зростанні n має кінцеву границю, тобто, якщо
при нескінченому зростанні n має кінцеву границю, тобто, якщо 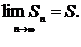 Число S називають сумою ряду. Якщо при
Число S називають сумою ряду. Якщо при 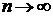 n – а частинна сума ряду не прямує до кінцевої границі, то ряд називають розбіжним.
n – а частинна сума ряду не прямує до кінцевої границі, то ряд називають розбіжним.
|
|
|
Ряд, що складається із членів будь-якої спадної геометричної прогресії
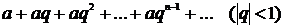 , збігається і має суму
, збігається і має суму  .
.
Так званий гармонійний ряд  розбігається.
розбігається.
Сформулюємо основні теореми про числові ряди:
1. Якщо збігається ряд  , то збігається і ряд
, то збігається і ряд
 , що складається із членів даного ряду, починаючи з
, що складається із членів даного ряду, починаючи з
(m + 1) - ого. Цей останній ряд називають залишком даного ряду. І навпаки: із збіжності ряду  випливає збіжність ряду
випливає збіжність ряду
 .
.
2. Якщо збігається ряд  і його сума дорівнює
і його сума дорівнює
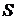 , то збігається і ряд
, то збігається і ряд 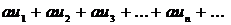 , причому його сума дорівнює
, причому його сума дорівнює 
3. Якщо збігаються ряди  і
і
 відповідно із сумами S і
відповідно із сумами S і 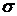 , то збігається ряд
, то збігається ряд
4
 , причому сумою останнього ряду буде S +
, причому сумою останнього ряду буде S + 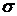 .
.
4. Якщо збігається ряд  , то
, то  ,
,
тобто при 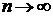 границя загального члена ряду дорівнює нулю (необхідна умова збіжності).
границя загального члена ряду дорівнює нулю (необхідна умова збіжності).

Виконання необхідної умови збіжності не є достатнім. Таким чином, якщо необхідна умова збіжності не виконується, констатуємо розбіжність ряду, а якщо виконується, - проводимо додаткове дослідження, перевіряючи виконання, так званих, достатніх умов збіжності (див. Тему 2).
Приклад. Обчислити суму ряду  .
.
|
|
|
Запишемо частинні суми ряду у вигляді, зручному для подальшого граничного переходу.

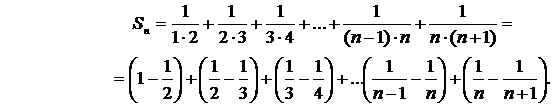
Після розкривання дужок одержуємо досить простий вираз для частинної суми:
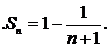
Знаходимо границю:

Таким чином, ряд збігається, а його сума дорівнює 1.
Зауважимо, що знаходження сум ряду за визначенням, тобто за допомогою границі послідовності частинних сум, дуже непроста задача, розв’зання якої, взагалі кажучи, суттєво залежить від того, у якому вигляді задається конкретний ряд. З іншого боку, при розгляді великої кількості проблем дослідника може цікавити лише питання збіжності або розбіжності ряду, а не сама його сума. Тому дослідження збіжності відбувається за допомогою спеціальної теорії (див. Тему 2), а сума ряду, якщо її обчислення виявляється важким за визначенням, знаходиться наближено. (Останнє питання не входить у коло проблем, що розглядаються у даних методичних вказівках).
5
Запитання для самоперевірки
1. Що таке числова послідовність, границя послідовності?
2. Що називається числовим рядом, членами ряду, сумою ряду, залишком ряду?
3. Збіжність найпростіших числових рядів: спадна геометрична прогресія, гармонічний ряд.
4. Необхідна умова збіжності. Яке співвідношення задає цю умову?
Домашнє завдання
1. Записати  для наведених нижче рядів, якщо відомі декілька їх перших членів:
для наведених нижче рядів, якщо відомі декілька їх перших членів:
а) 
б) 
в) 
г) 
д) 
ж) 
2. Записати 4 – 5 перших членів ряду, якщо відомо загальний член 
а)  б)
б)  в)
в)  г)
г) 
3. Переконатись в розбіжності ряду, застосовуючи необхідну ознаку збіжності:

4. №№ 2773, 2778 [3].
6
РЯДИ З ДОДАТНИМИ ЧЛЕНАМИ. ОЗНАКИ ПОРІВНЯННЯ . ОЗНАКИ ДАЛАМБЕРА І КОШІ. ІНТЕГРАЛЬНА ОЗНАКА КОШІ-МАКЛОРЕНА
Сформулюємо найважливіші ознаки збіжності і розбіжності рядів із додатними членами.
Теорема. Нехай 
 два ряди з додатними членами. Тоді:
два ряди з додатними членами. Тоді:
1) якщо 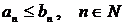 , то із збіжності ряду
, то із збіжності ряду  випливає збіжність ряду
випливає збіжність ряду
 а із розбіжності ряду
а із розбіжності ряду  - розбіжність ряду
- розбіжність ряду  ;
;
2) якщо  >0, то обидва ряди збіжні або розбіжні одночасно.
>0, то обидва ряди збіжні або розбіжні одночасно.
При дослідженні рядів на збіжність користуються, так званими, “еталонними” рядами, тобто рядами збіжність або розбіжність яких завчасно відома. З цією метою часто використовують такі ряди, як
 і
і
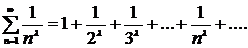
До речі, останній ряд збіжний при  і розбіжний при
і розбіжний при 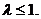
Приклади. Дослідити збіжність рядів:
1.  Скористаємось ознакою порівняння. Порівняємо даний ряд із гармонійним:
Скористаємось ознакою порівняння. Порівняємо даний ряд із гармонійним:  Так як виконується нерівність
Так як виконується нерівність  ,
,
досліджуваний ряд розбіжний.
2. 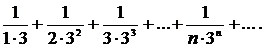
7
Для порівняння вибираємо нескінченно спадну геометричну прогресію  зі знаменником
зі знаменником  . Так як виконується нерівність
. Так як виконується нерівність  , то досліджуваний ряд збіжний.
, то досліджуваний ряд збіжний.
3. 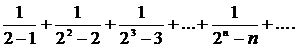 Для порівняння вибираємо ряд
Для порівняння вибираємо ряд
 . Скористаємось теоремою порівняння: Так як ряд
. Скористаємось теоремою порівняння: Так як ряд  - збіжний, то і даний ряд збігається.
- збіжний, то і даний ряд збігається.
Збіжність ряду з додатними членами  ,
,  досліджується також за допомогою інших ознак збіжності.
досліджується також за допомогою інших ознак збіжності.
Ознака Даламбера. Якщо існує скінчена границя 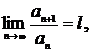 то при l < 1 ряд
то при l < 1 ряд  збіжний, при l > 1 ряд розбіжний, при l = 1 ознака не дає відповіді про збіжність чи розбіжність ряду і потрібні додаткові дослідження.
збіжний, при l > 1 ряд розбіжний, при l = 1 ознака не дає відповіді про збіжність чи розбіжність ряду і потрібні додаткові дослідження.
Приклади. 1. 
Скористаємось ознакою Даламбера. 
 Отже ряд
Отже ряд  - збіжний.
- збіжний.
2.  Застосуємо ознаку Даламбера.
Застосуємо ознаку Даламбера.

Ознака Даламбера не дає відповіді на питання про збіжність ряду. У даному
разі більш ефективно буде діяти ознака порівняння. Отже порівняємо даний
8
ряд із збіжним рядом 
 За теоремою порівняння:
За теоремою порівняння:
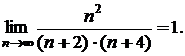 Таким чином, даний ряд збіжний.
Таким чином, даний ряд збіжний.
Радикальна ознака Коші. Нехай  (
(  ) і
) і  Тоді ряд
Тоді ряд  збіжний, якщо
збіжний, якщо  і розбіжний, якщо
і розбіжний, якщо 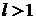 . У випадку, якщо
. У випадку, якщо 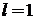 питання про збіжність ряду залишається відкритим.
питання про збіжність ряду залишається відкритим.
Приклад.Дослідити збіжність ряду  .
.
Оскільки  то даний ряд збіжний.
то даний ряд збіжний.
Інтегральна ознака Коші - Маклорена. Якщо  при
при 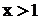 додатна, монотонно спадна і неперервна, то
додатна, монотонно спадна і неперервна, то
ряд  , де
, де 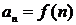 збігається або розбігається у залежності від того, чи є невласний інтеграл
збігається або розбігається у залежності від того, чи є невласний інтеграл  збіжним або розбіжним.
збіжним або розбіжним.
Приклад.Дослідити збіжність ряду

Функція  додатна, монотонно спадна в неперервна на проміжку
додатна, монотонно спадна в неперервна на проміжку  . Дослідимо інтеграл
. Дослідимо інтеграл

Таким чином, невласний інтеграл збіжний. Тобто за інтегральною ознакою Коші – Маклорена даний ряд також є збіжний.
При дослідженні збіжності числового ряду з додатними членами треба
9
вміло підбирати відповідну ознаку. Рекомендується починати дослідження з перевірки виконання необхідної умови збіжності ряду. Якщо необхідна умова збіжності ряду не виконується, ряд розбігається. Якщо вона виконується, треба обов’язково перевірити, чи виконуються достатні умови, тобто використати або ознаку порівняння, або ознаку Даламбера, або радикальну ознаку Коші, або інтегральну ознаку Коші – Маклорена. Найпростіша з цих ознак - ознака Даламбера. У випадку, коли ця ознака не працює, треба подивитись, чи можливо підібрати ряд для порівняння. Це може бути знайомий ряд (наприклад, сума нескінченно спадної геометричної прогресії, гармонійний ряд і т.и.), або ряд, який дослідити легше, ніж даний. Якщо легко знайти корінь ступеня n із  , бажано використати радикальну ознаку Коші. Якщо ви можете легко інтегрувати
, бажано використати радикальну ознаку Коші. Якщо ви можете легко інтегрувати  , як функцію n, то найкращий вибір – це інтегральна ознака Коші – Маклорена.
, як функцію n, то найкращий вибір – це інтегральна ознака Коші – Маклорена.
Запитання для самоперевірки
1. Сформулювати три теореми про властивості збіжних рядів з додатними членами.
2. Необхідні і достатні умови збіжності ряду.
3. Сформулювати теореми порівняння.
4. Сформулювати ознаки Даламбера, Коші (радикальний), Коші – Маклорена (інтегральний).
Домашнє завдання
1. №№2778, 2754, 2782, 2783, 2760, 2777, 2757, 2763, 2764, 2766, 2767, 2769, 2740, 2771, 2748, 2781, 2752*, 2745* [3].
3. ЗНАКОЗМІННІ РЯДИ. АБСОЛЮТНА ТА УМОВНА ЗБІЖНІСТЬ РЯДУ. ОЗНАКА ЛЕЙБНІЦА. ТЕОРЕТИЧНІ ВІДОМОСТІ
Ряд вигляду  , де
, де 
(n=1, 2, 3, …) є ряд, знаки членів якого чергуються.
Ознака Лейбніца. Ряд  збігається, якщо виконуються дві умови:
збігається, якщо виконуються дві умови:
1) 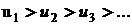 і 2)
і 2) 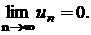
Якщо деякий ряд задовольняє ознаці Лейбніца, то його називають збіжним умовно.
Знакозмінним рядом називається ряд, членами якого є числа довільного знаку. Такий ряд із довільним чергуванням знаків його членів
10

збігається, якщо збігається ряд

У цьому випадку ряд  називається абсолютно збіжним.
називається абсолютно збіжним.
Якщо ряд  збігається абсолютно, то ряд, одержаний після будь-якої перестановки його членів, буде збігатися абсолютно і мати ту ж саму суму, що і первісний ряд.
збігається абсолютно, то ряд, одержаний після будь-якої перестановки його членів, буде збігатися абсолютно і мати ту ж саму суму, що і первісний ряд.
Якщо ряд  збігається умовно, то при перестановці нескінченної кількості його членів сума ряду може змінитися. А в деяких випадках при відповідній перестановці членів умовно збіжного ряду можна одержати розбіжний ряд.
збігається умовно, то при перестановці нескінченної кількості його членів сума ряду може змінитися. А в деяких випадках при відповідній перестановці членів умовно збіжного ряду можна одержати розбіжний ряд.
Приклади.1.Дослідити збіжністьзнакозмінного ряду:
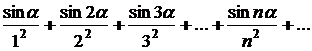 .
.
Складемо ряд із абсолютних величин членів цього ряду:
 . Це ряд з додатними членами. Має місце нерівність
. Це ряд з додатними членами. Має місце нерівність  Ряд
Ряд  - збіжний. Отже за
- збіжний. Отже за
теоремою порівняння ряд  теж збіжний, а значить досліджуваний ряд збігається абсолютно.
теж збіжний, а значить досліджуваний ряд збігається абсолютно.
Рекомендується завжди починати дослідження знакозмінних рядів з перевірки, чи має місце абсолютна збіжність. У теорії доведено, що абсолютна збіжність сильніша, ніж умовна: якщо ряд збігається абсолютно, для нього завжди виконуються умови ознаки Лейбніца. Лише якщо абсолютної збіжності немає, перевіряємо, чи є умовна, тобто чи задовольняє ряд ознаці Лейбніца. Ряд вважається розбіжним, якщо він не має навіть умовної збіжності.
2. Дослідити збіжність ряду:  .
.
11
Складемо ряд з абсолютних величин членів даного ряду. Одержимо ряд з додатними членами:

Ми одержали узагальнений гармонійний ряд з показником  . Це розбіжний ряд. Отже ряд з абсолютних величин членів даного ряду розбіжний. У той же час умови ознаки Лейбніца виконуються:
. Це розбіжний ряд. Отже ряд з абсолютних величин членів даного ряду розбіжний. У той же час умови ознаки Лейбніца виконуються:

Таким чином, даний ряд збігається умовно.
Запитання для самоперевірки
1. Який ряд називається знакозмінним?
2. Дайте визначення абсолютної і умовної збіжності ряду.
3. В чому полягає ознака Лейбніца?
4. У якій послідовності доцільно аналізувати поведінку знакозмінних рядів?
Домашнє завдання
№№2790, 2791, 2782, 2794, 2795, 2796, 2797 [3].
Дата добавления: 2018-02-15; просмотров: 2977; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
