ФУНКЦІОНАЛЬНІ РЯДИ. СТЕПЕНЕВІ РЯДИ
Ряд 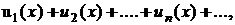 члени якого – функції від х, називається функціональним рядом. Сукупність значень х, для яких функції
члени якого – функції від х, називається функціональним рядом. Сукупність значень х, для яких функції 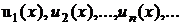 визначені і ряд
визначені і ряд  - збігається, називають областю збіжності функціонального ряду. Областю збіжності функціонального ряду частіше всього буває деякий проміжок осі Ох.
- збігається, називають областю збіжності функціонального ряду. Областю збіжності функціонального ряду частіше всього буває деякий проміжок осі Ох.
Кожному значенню з області збіжності Х відповідає певне значення величини  . Цю величину, що є функцією х, будемо називати сумою функціонального ряду і позначати її через
. Цю величину, що є функцією х, будемо називати сумою функціонального ряду і позначати її через 
Представимо  у вигляді
у вигляді  де
де  ,
,
12
 . (
. (  - залишок функціонального ряду).
- залишок функціонального ряду).
Збіжний функціональний ряд  називається рівномірно збіжним у деякий області Х , якщо для кожного скільки завгодно малого числа
називається рівномірно збіжним у деякий області Х , якщо для кожного скільки завгодно малого числа 
 існує таке ціле додатне число
існує таке ціле додатне число  , що при
, що при  виконується нерівність
виконується нерівність  для усякого х з області Х. Корисно мати на увазі, що сума
для усякого х з області Х. Корисно мати на увазі, що сума  рівномірно збіжного ряду
рівномірно збіжного ряду  у області Х, де
у області Х, де  - неперервні функції, є неперервна функція.
- неперервні функції, є неперервна функція.
Сформулюємо достатню ознаку рівномірної збіжності – ознаку Вейерштрасса.
Якщо функції  у деякій області Х не перевищують за абсолютною величиною додатних чисел
у деякій області Х не перевищують за абсолютною величиною додатних чисел  причому числовий ряд
причому числовий ряд  збігається, то функціональний ряд
збігається, то функціональний ряд  в цій області збігається рівномірно.
в цій області збігається рівномірно.
Функціональний ряд вигляду  де
де  - дійсні числа називається степеневим.
- дійсні числа називається степеневим.
Теорема Абеля. Якщо степеневий ряд збігається при х = х0, то він буде збігатись (і при цьому абсолютно) при всякому значенні х, що задовольняє нерівність

Одним з наслідків теореми Абеля є факт існування для всякого степеневого ряду інтервалу збіжності с центром у точці а  у якому степеневий ряд збігається абсолютно і за межами якого розбігається. На кінцях інтервалу збіжності (у точках
у якому степеневий ряд збігається абсолютно і за межами якого розбігається. На кінцях інтервалу збіжності (у точках  ) різні степеневі ряди поводять себе по-різному: деякі збігаються
) різні степеневі ряди поводять себе по-різному: деякі збігаються
абсолютно на обох кінцях, інші або збігаються умовно на обох кінцях, або на одному з них збігаються умовно, а на другому розбігаються, також
зустрічаються ряди, які розбігаються на обох кінцях.
Число R – половина довжини інтервалу збіжності – називається радіусом збіжності степеневого ряду.
У деяких випадках радіус збіжності може дорівнювати нулюві або нескінченності.
Якщо R = 0, то степеневий ряд збігається тільки при х = а, якщо R =  , то ряд збігається на усій числовій осі.
, то ряд збігається на усій числовій осі.
13
Для розшуку інтервалу і радіусу збіжності степеневого ряду можна використовувати один з наступних способів:
1. Якщо серед коефіцієнтів ряду  немає рівних нулю (тобто ряд містить усі цілі додатні ступені різниці (х – а)), то
немає рівних нулю (тобто ряд містить усі цілі додатні ступені різниці (х – а)), то 
2. Якщо 
де р – деяке ціле додатне число, то

3. Якщо серед коефіцієнтів ряду є рівні нулю і послідовність показників ступенів (х - а), що залишились, довільна, то радіус збіжності можна находити за формулою:
 ,
,
в який використовуються тільки значення  , що відмінні від нуля. (Зауважимо, що ця формула може бути використана у випадках 1) і 2).
, що відмінні від нуля. (Зауважимо, що ця формула може бути використана у випадках 1) і 2).
4. В усіх випадках інтервал збіжності можна знаходити, використовуючи ознаку Даламбера або радикальну ознаку Коші до ряду, складеному із абсолютних величин членів даного ряду.
Записавши ряд у вигляді  (де
(де  залежність N від n будь- яка, аn - це коефіцієнт при (х – а)n, а коефіцієнт n – ого члена ряду), знаходимо інтервал збіжності із нерівностей:
залежність N від n будь- яка, аn - це коефіцієнт при (х – а)n, а коефіцієнт n – ого члена ряду), знаходимо інтервал збіжності із нерівностей: 
В л а с т и в о с т і с т е п е н е в и х р я д і в. Ряди, що одержані шляхом операцій диференціювання і інтегрування степеневого ряду, мають той же інтервал збіжності, що і даний ряд, і їх сума в межах інтервалу збіжності дорівнює відповідно похідній і інтегралу від суми даного ряду.
Якщо
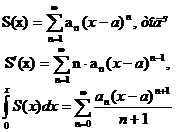

14
Операцію диференціювання і інтегрування можна проводити над степеневим рядом скільки завгодно разів. Таким чином, сума степеневого ряду у межах його інтервалу збіжності нескінченно диференційована.
Приклади. Знайти інтервали збіжності степеневих рядів і дослідити їх збіжність на кінцях інтервалів збіжності.
1. 
 .
.
Парні коефіцієнти дорівнюють нулю. Тому для знаходження інтервалу збіжності доцільно застосувати ознаку Даламбера.

Згідно з ознакою Даламбера ряд збіжний, якщо 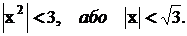
Таким чином, радіус збіжності даного ряду дорівнює  а інтервал збіжності
а інтервал збіжності  Дослідимо поведінку ряду на кінцях інтервалу збіжності. При
Дослідимо поведінку ряду на кінцях інтервалу збіжності. При  одержуємо ряд
одержуємо ряд  при
при  - ряд
- ряд  Обидва ці ряди розбіжні, тому що для них не виконується необхідна умова збіжності рядів. Отже інтервал збіжності – відкритий:
Обидва ці ряди розбіжні, тому що для них не виконується необхідна умова збіжності рядів. Отже інтервал збіжності – відкритий: 
2. 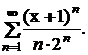 Маємо
Маємо  Знайдемо радіус збіжності:
Знайдемо радіус збіжності:

Звідси - 2 < x +1 <2, - 3 < x < 1. При x = - 3 маємо ряд 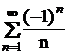 ,
,
який збігається умовно (за ознакою Лейбніца), при x = 3 одержимо гармонійний ряд  , що розбігається. Остаточно маємо такий інтервал збіжності:
, що розбігається. Остаточно маємо такий інтервал збіжності: 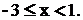
3.  .
.
15
У даному випадку маємо: 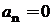 при
при  при
при  Для розшуку радіуса збіжності доцільно скористатись формулою:
Для розшуку радіуса збіжності доцільно скористатись формулою:

Знаходимо:

Дослідимо ряд на кінцях інтервалу збіжності. Нехай  . Одержимо числовий ряд:
. Одержимо числовий ряд:

Але  Таким чином, при
Таким чином, при  ряд розбігається. Те ж саме буде при
ряд розбігається. Те ж саме буде при  . Тому область збіжності даного ряду
. Тому область збіжності даного ряду 
4. 
Застосуємо радикальну ознаку Коші: 

Таким чином, ряд збігається, якщо  , тобто при
, тобто при 
5. Знайти суму ряду  шляхом диференціювання ряду
шляхом диференціювання ряду 
Застосуємо формулу суми членів нескінченної спадної геометричної
16
прогресії:
 Одержуємо:
Одержуємо: 
Залишається знайти похідну останнього співвідношення:

Завдання для самоперевірки
1. Сформулюйте визначення функціонального ряду, степеневого ряду.
2. Що представляє собою радіус збіжності? Які є способи розшуку радіуса збіжності степеневого ряду?
3. Дайте визначення інтервалу збіжності степеневого ряду. Як досліджуються степеневі ряди на кінцях інтервалу збіжності?
Домашнє завдання
Дослідити збіжність рядів: 1)  2)
2) 
РЯДИ ТЕЙЛОРА І МАКЛОРЕНА
Усяка функція, що має безліч похідних у інтервалі 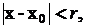 може бути розкладена у цьому інтервалі у збіжний до неї нескінченний ряд Тейлора
може бути розкладена у цьому інтервалі у збіжний до неї нескінченний ряд Тейлора

якщо у цьому інтервалі виконується умова 
 це, так званий, залишковий член формули Тейлора,
це, так званий, залишковий член формули Тейлора, 
При 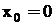 одержуємо ряд Маклорена:
одержуємо ряд Маклорена:

17
Якщо у деякому інтервалі, що містить точку х0, при будь-якому п виконується нерівність  де
де  - додатна стала, то
- додатна стала, то  і функція
і функція  розкладається у ряд Тейлора.
розкладається у ряд Тейлора.
Наведемо відомі розклади у ряди Тейлора наступних функцій:
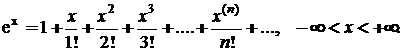
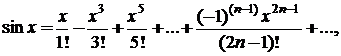
 .
.

 .
.
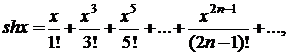
 .
.

 .
.

Останнє співвідношення виконується:
при  якщо
якщо 
при  якщо
якщо 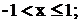
при  якщо
якщо 


Приклади.1. Розкласти у степеневий ряд функцію 
Розв’язок. Знайдемо значення функції і її похідних при 
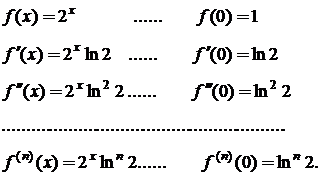
18
Так як  то при фіксованому х має місце нерівність
то при фіксованому х має місце нерівність
 при усіх n. Таким чином, шуканий ряд у даному випадку
при усіх n. Таким чином, шуканий ряд у даному випадку

Цей же ряд можна було б одержати, користуючись відомим розкладом для 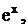 у якому треба х замінити на
у якому треба х замінити на 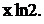 (Користуємось відомим
(Користуємось відомим
співвідношенням  ).
).
2. Розкласти  у ряд по ступенях х – 2.
у ряд по ступенях х – 2.
Розв’язок. Скористаємось рівністю  Праву частину рівності можна розглядати як суму нескінченної спадної геометричної прогресії з першим членом
Праву частину рівності можна розглядати як суму нескінченної спадної геометричної прогресії з першим членом  і знаменником
і знаменником  Звідси маємо:
Звідси маємо:
 або
або

Збіжність ряду має місце, якщо  або 0 < x < 4.
або 0 < x < 4.
3. Розкласти у степеневий ряд функцію 
Розв’язок. Розклад можна одержати двома шляхами. По-перше, використовуючи стандартну схему, пов’язану з диференціюванням даної функції 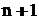 раз, фіксуванням одержаних похідних у точці х = 0 і підставляючи одержані значення у формулу Маклорена. По-друге, є більш раціональний підхід, пов’язаний із використанням відомих формул.
раз, фіксуванням одержаних похідних у точці х = 0 і підставляючи одержані значення у формулу Маклорена. По-друге, є більш раціональний підхід, пов’язаний із використанням відомих формул.
У рівності  замінюємо функцію
замінюємо функцію  розкладом у степеневий ряд:
розкладом у степеневий ряд:
19

Виконавши неважкі перетворення, одержимо бажаний розклад.
Отже, якщо розклад у степеневий ряд Тейлора або Маклорена існує, одержати його неважко, якщо використати відповідні формули безпосередньо, або скористатися відомими розкладами і, якщо необхідно, потрібними формулами із тригонометрії.
Запитання для самоперевірки
1. Яким умовам повинна задовольняти функція, щоб її можна було розкласти у ряд Тейлора або Маклорена?
2. Розкласти функції у ряди Маклорена, користуючись відомими розкладами:
а)  б)
б)  в)
в) 
Дата добавления: 2018-02-15; просмотров: 2077; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
