Свойства операций над множествами
Множества. Основные понятия и определения.
Множество- совокупность некоторых объектов, объединенных по заданному признаку.
Множество обозначается большой буквой латинского алфавита, а его элементы маленькой. Принадлежность элемента a множеству A обозначается:
a  A
A
В качестве примеров множеств можно назвать множество студентов вуза, множество животных определенного вида, множество точек кривой на плоскости, множество футбольных команд российской премьер-лиги и т.п.
Мощность множестваравна количеству элементов множества.
Дискретное множество- это прерывное множество, т.е группа студентов: Петров, Иванов и Сидоров.
Подмножества- множество В называется подмножеством множества А, если его каждый элемент входит в множество А.
Подмножество может состоять из 1,2 или более элементов. Множество, не содержащее предметы, называется пустое множество, оно является подмножеством любого множества.
N=2n- количество подмножеств.
Основные числовые множества:
1. N- Натуральные числа (1,2,3,…)
2. Z- Целые числа (0,+/-1,+/-2,+/-3,…)
3. Рациональные числа  , где р-целое число, q-целое число
, где р-целое число, q-целое число
4.R- множество действительных чисел (-  ; +
; +  )
)
5. Числовой интервал, т.е. число х, заключенное между а и в
2. Виды множеств:
Конечное- множество, количество элементов которого конечно, то есть, существует неотрицательное целое число k, равное количеству элементов этого множества
|
|
|
Бесконечное- множество, не являющееся конечным
Пустое- Множество, не содержащее предметы
Универсальное- это множество, которому принадлежат все элементы рассматриваемых множеств.
Основные операции над множествами
1) Объединение множеств. Результатом объединения множеств A и B будет являться множество C такое, что любой элемент множества C является элементом либо множества A, либо множества B.
Операция объединения множеств обозначается следующим образом:
А  В
В
2) Пересечение множеств Результатом пересечения множеств A и B будет являться множество C такое, что любой элемент множества C является одновременно и элементом множества A, и элементом множества B. Операция пересечения множеств обозначается следующим образом:
А 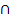 В
В
3) Разность множеств Результатом разности множеств A и B будет являться множество C такое, что любой элемент множества C является элементом множества A, и не является элементом множества B. Операция разность множеств обозначается следующим образом:
А  В
В
4) Дополнением множества A до множества B будет являться множество C такое, что любой элемент множества C является элементом множества B, и не является элементом множества A. Операция дополнения множества обозначается следующим образом:
|
|
|
В  А
А
5) Сравнение множеств. А=В, если оба состоят из одних и тех же элементов.
Свойства операций над множествами

Дата добавления: 2018-02-15; просмотров: 1726; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
