Логические операции над высказываниями.
- Отрицание.
Отрицанием высказывания х называется новое высказывание, которое является истинный, если высказывание х ложно, и ложным, если высказывание xистинно. Отрицание высказывания х обозначается 
и читается «не х»или «неверно, что х».
Логические значения высказывания х можно описать с помощью таблицы:
| x | 
|
| 0 | 1 |
| 1 | 0 |
Таблицы такого вида принято называть таблицамиистинности.
Пусть х высказывание. Так как также является высказыванием, то можно образовать отрицание высказывания , то есть высказывание 
, которое называется двойным отрицанием высказывания х.
2. Конъюнкция (логическое умножение).
Конъюнкцией двух высказываний х, у называется новое высказывание, которое считается истинным, если оба высказывания х, у истинны, и ложным, если хотя бы одно из них ложно.
Конъюнкция высказываний х, у обозначается символом х&у или (х 
у), читается «x и у». Высказывания х, у называются членами конъюнкции.
Логические значения конъюнкции описываются следующей таблицей истинности:
| x | y | х&у |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Например, для высказываний «6 делится на 2», «б делится на 3» их конъюнкцией будет высказывание «б делится на 2 и 6 делится на 3», которое, очевидно, истинно.
Из определения операции конъюнкции видно, что союз «и» в алгебре логики употребляется в том же смысле, что и в повседневной речи. Но в обычной речи не принято соединять союзом «и» два высказывания далеких друг от Друга по содержанию, а в алгебре логики рассматривается конъюнкция двух любых высказываний.
|
|
|
Из определения операции конъюнкции и отрицания ясно, что высказывание x& всегда ложно.
3. Дизъюнкция (логическое сложение).
Дизъюнкцией двух высказываний х, у называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний x, у истинно, и ложным, если они оба ложны.
Дизъюнкция высказываний х, у обозначается символом x 
y, читается «x или у». Высказывания х, у называются членами дизъюнкции.
Логические значения дизъюнкции описываются следующей таблицей истинности:
| х | y | 
|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Например, высказывание «В треугольнике DFE угол D или угол Е острый» истинно, так как обязательно истинно хотя бы одно из высказываний: «В треугольнике DFE угол D острый», «В треугольнике DFE угол Е острый».
В повседневной речи союз «или» употребляется в различном смысле: исключающем и не исключающем (жизнь или смерть). В алгебре логики союз «или» всегда употребляется в не исключающем смысле.
4. Импликация.
Импликацией двух высказываний х, у называется новое высказывание, которое считается ложным, если х истинно, а у - ложно, и истинным во всех остальных случаях.
|
|
|
Импликация высказываний х, у обозначается символом х 
у, читается «если х, то у» или «из х следует у». Высказывание хназывают условием или посылкой, высказывание у — следствием или заключением, высказывание х у - следованием или импликацией.
Логические значения операции импликации описываются следующей таблицей истинности:
| x | x | х  y
|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Например, высказывание «Если число 12 делится на 6, то оно делится на 3», очевидно, истинно, так как здесь истинна посылка «Число 12 делится на 6» и истинно заключение «Число 12 делится на 3». «Если 2 x 2=5, то существует баба яга »
Употребление слов «если .,., то ...» в алгебре логики отличается от употребления их в обыденной речи, где мы, как правило, считаем, что, если высказывание х ложно, то высказывание «Если х, то у» вообще не имеет смысла. Кроме того, строя предложение вида «если х, то у» в обыденной речи, мы всегда подразумеваем, что предложение у вытекает из предложения х.Употребление слов «если ..., то ...» в математической логике не требует этого, поскольку в ней смысл высказываний не рассматривается.
|
|
|
5. Эквивалеация.
Эквиваленцией (или эквивалентностью) двух высказываний х, у называется новое высказывание, которое считается истинным, когда оба высказывания д:, у либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.
Эквиваленция высказываний х, у обозначается символом х 
у, читается «для того, чтобы х, необходимо и достаточно, чтобы y» или «х тогда и только тогда, когда у». Высказывания х, у называются членами эквиваленции. Логические значения операции эквиваленцин описываются следующей таблицей истинности:
| х | y | х  у
|
| *1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Например, эквиваленция «Треугольник SPQ с вершиной S и основанием PQ равнобедренный тогда и только тогда, когда SP=SQ» является истинной, так как высказывания «Треугольник SPQ с вершиной S и основанием PQ равнобедренный» и «В треугольнике SPQ с вершиной S и основанием PQ SP = SQ » либо одновременно истинны, либо одновременно ложны. Эквивалентность играет важную роль в математических доказательствах. Известно, что значительное число теорем формулируется в форме необходимых и достаточных условий, то есть в форме эквивалентности. В этом случае, зная об истинности или ложности одного из двух членов эквивалентности и доказав истинность самой эквивалентности, мы заключаем об истинности или ложности второго члена эквивалентности.
|
|
|
- Сложение по модулю два
.
Функция сложения по модулю два истинна тогда и только тогда, когда значения переменных различны.
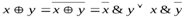(8)
| x | y |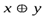 
|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- Стрелка Пирса.
Запись 
читается как «x стрелка Пирса y». Функция истина тогда и только тогда, когда ложны обе её переменные.
| x | y | 
|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Cтрелка Пирса противоположна дизъюнкции, и для неё справедливо:
(9)
- Функция Шеффера.
Запись 
x|y читается как «x штрих Шеффера y». Функция ложна тогда и только тогда, когда оба значения переменных истинны.
| x | y | 
|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Штрих Шеффера противоположна конъюнкции, и для неё справедливо:
(10)
С помощью логических операций над высказываниями из заданной совокупности высказываний можно строить различные сложные высказывания. При этом порядок выполнения операций указывается скобками. Например, из трех высказываний х, у, гможно построить высказывания:
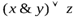и
Первое из них есть дизъюнкция конъюнкции х, у, а второе высказывание есть импликация, посылкой которой является высказывание х, а заключением - отрицание дизъюнкции высказывания у и конъюнкции высказываний х, z.
Формулой алгебры логикиназываетсявсякое сложное высказывание, которое может быть получено из элементарных высказываний посредством применения логических операций отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции.
Формулы алгебры логики будем обозначать большими буквами латинского алфавита А, В, С, ...
Для упрощения записи формул принят ряд соглашений. Скобки можно опускать, придерживаясь следующего порядка действий: конъюнкция выполняется раньше, чем все остальные операции, дизъюнкция выполняется раньше, чем импликация и эквивалентность. Если над формулой стоит знак отрицания, то скобки тоже опускаются.
Логическое значение формулы алгебры логики полностью определяется логическими значениями входящих в нее элементарных высказываний.
Все возможные логические значения формулы, в зависимости от значений входящих в нее элементарных высказываний, могут быть описаны полностью с помощью таблицы истинности.
Например, для формулы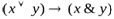 
таблица истинности:
| x | y | 
| х&у | 
|
| 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 |
Легко видеть, что, если формула содержит п элементарных высказываний, то она принимает 
значений, состоящих из нулей и единиц, или, что то же, таблица содержит строк .
Определение. Две формулы алгебры логики А и В называются равносильными, если они принимают одинаковые логические значения на любом наборе значений входящих в формулы элементарных высказываний.
Равносильность формул будем обозначать знаком 
, а запись А В означает, что формулы А и В равносильны.
Например, равносильны формулы:
Формула А называется тождественно истинной(или тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных.
Например, тожественно истинны формулы:
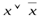
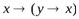
Формула А называется тождественно ложной, если она принимает значение О при всех значениях входящих в нее переменных.
Например, тождественно ложна формула:
Ясно, что отношение равносильности рефлексивно, симметрично и транзитивно,
Между понятиями равносильности и эквивалентности существует следующая связь: если формулы А и В равносильны, то формула А В - тавтология, и обратно, если формула 
- тавтология, то формулы А и В равносильны.
Как уже отмечалось, значение формулы алгебры логики полностью зависит от значений входящих в эту формулу высказываний. Поэтому формула алгебры логики является функцией входящих в нее элементарных высказываний.
Например, формула: 
является функцией трех переменных 
.
Определение. Функцией алгебры логики п переменных (или функцией Буля) называется функция п переменных, где каждая переменная принимает два значения: 0 в 1, и при этом функция может принимать только одно из двух значений: 0 или 1.
Ясно, что тождественно истинные и тождественно ложные формулы алгебры логики представляют собой постоянные функции, а две равносильные формулы выражают одну и ту же функцию.
Выясним, каково число функций п переменных. Очевидно, каждую функцию алгебры логики (как и формулу алгебры логики) можно задать с помощью таблицы истинности, которая будет содержать строк. Следовательно, каждая функция ппеременных принимает значений, состоящих из нулей и единиц. Таким образом, функция n переменных полностью определяется набором значений из нулей и единиц длины . Общее же число наборов, состоящих из нулей и единиц, длины равно . Значит, число различных функций алгебры логики n переменных равно .
В частности, различных функций одной переменной четыре, а различных функций двух переменных шестнадцать. Выпишем все функции алгебры логики одной и двух переменных.
Дата добавления: 2018-02-15; просмотров: 793; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!