ЭНТРОПИЯ И ЕЕ СВОЙСТВА. ОПРЕДЕЛЕНИЕ САМОПРОИЗВОЛЬНОСТИ И РАВНОВЕСИЯ ПРОЦЕССОВ В ИЗОЛИРОВАННЫХ СИСТЕМАХ

⇐ ПредыдущаяСтр 9 из 18Следующая ⇒

Физическим смыслом понятия энтропии является мера хаоса в системе; мера той энергии, которая рассеивается в виде тепла и не превращается в работу ("связанная энергия"). Энтропия является функцией состояния системы и не зависит от пути перехода. Ее изменение определяется только начальным и конечным состоянием. Размерность энтропии (СИ): . Энтропия зависит от массы тела и в ходе процесса она суммируется (аддитивная величина), т.е. обладает экстенсивными свойствами.

Согласно второму закону термодинамики изменение энтропии в квазистатическом (равновесном) процессе

(2.1.1)

т.е. изменение энтропии происходит под действием энергии, передаваемой в виде теплоты и равно приведенной теплоте .

Следствием второго закона термодинамики являются соотношения

dQ_необр < dQ_обр (2.1.2)

dW_необр < dW_обр

Т.е. работа любого необратимого процесса всегда меньше работы обратимого процесса между теми же начальным и конечным состояниями системы. Поэтому работу в обратимых процессах называют максимальной работой

W_обр = W_max (2.1.3)

Чем меньше работа по сравнению с максимальной, тем более необратим процесс. Процессы, которые происходят без совершения работы, являются полностью необратимыми.

Теплота в необратимом процессе также меньше, чем в обратимом.

Таким образом, для необратимых (нестатических) процессов

dS > (2.1.4)

Свойства энтропии.

1)Энтропия – функция состояния; она имеет ту же размерность, что и теплоемкость: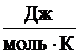

2) Энтропия– понятие вероятностное, поэтому и второй закон термодинамики имеет статистический характер, энтропия связана с термодинамической вероятностью в формуле Больцмана:

S = kℓnW, (2.1.5)

где k – постоянная Больцмана; k = 1,38 × 10^-23 Дж/K;

w – термодинамическая вероятность – число микросостояний, при помощи которых реализуется данное макросостояние.

Уравнение Больцмана можно представить и в другом виде:

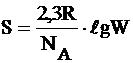, (2.1.6)

где R – универсальная газовая постоянная; R = 8,31441 ;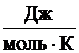

N_A – число Авогадро; N_A = 6,02204 × 10²³ моль^{– 1}.

3) Энтропия – экстенсивное свойство системы, зависящее от количества вещества в системе

Увеличение массы в n раз во столько же раз увеличивает энтропию.

4) Энтропия зависит от агрегатного состояния вещества.

5) S– величина аддитивная

S = S₁+ S₂ + … S_n.

Вычисление энтропии:

Изменение энтропии в химической реакции равно разности между энтропией продуктов реакции и энтропией исходных веществ

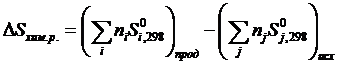(2.1.7)

Если проводить расчет энтропии в условиях, отличных от стандартных, то:

(2.1.8)

Объединив I и II начала термодинамики, получим фундаментальное уравнение термодинамики (уравнение Гиббса) для закрытых систем:

dU £ TdS – pdV –dW^/ (2.1.9)

где W^/' – все виды работ, совершаемые системой.

Уравнение (9) для закрытых систем, не способных совершать полезную работу:

dU £ TdS – PdV (2.1.10)

Если считать, что вся сообщаемая системе энергия идет на приращение внутренней энергии и на работу, совершаемую системой, то фундаментальное уравнение для равновесных процессов примет вид:

dU = TdS –– dW^/' (2.1.11)

Уравнения (2.1.9 – 2.1.11) представляют собой различные варианты фундаментального уравнения термодинамики и позволяют связать изменение внутренней энергии системы с возможностью протекания равновесного и самопроизвольного процессов.

Изменение энтропии вычисляют по следующим уравнениям:

1. Изменение энтропии при нагревании n молей любого вещества от температуры Т₁ до Т₂ при P = const рассчитывается по формуле

. (III,2)

Если зависимость С_Р от температуры описывается выражением

C_p = a + bT + сT²,

то

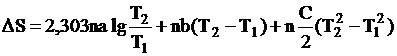, (III,3)

2. Изменение энтропии при фазовом переходе рассчитывается по формуле

, (III,4)

где ΔН – теплота фазового перехода одного моля вещества; Т – абсолютная температура фазового перехода.

3. Изменение энтропии при переходе n молей идеального газа из одного состояния в другое вычисляется по уравнениям:

, (III,5)

или

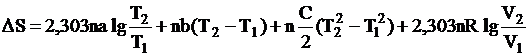, (III,6)

или

, (III,7)

где V₁, P₁, T₁ и V₂, P₂, T₂ – объем, давление, температура, характеризующие начальное и конечное состояние идеального газа соответственно; С_Р и С_V – соответственно истинные мольные теплоемкости идеального газа при постоянных давлении и объеме: .

4. Изменение энтропии в процессе диффузии при смешении газов (при Р = const и Т = const), т.е. в изотермно-изобарном процессе, вычисляются по уравнению

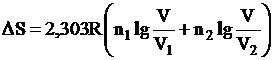(III,8)

или

, (III,9)

где n₁, n₂ – число молей первого и второго газа; N₁ и N₂ – мольные доли обоих газов; V₁ и V₂ – начальные объемы обоих газов; V – конечный объем смеси газов (V = V₁ + V₂).

5. Вычисление изменения энтропии по электрохимическим данным по уравнению

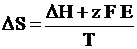, (III,10)

где Н – тепловой эффект химической реакции; F – число Фарадея; Е – электродвижущая сила (э.д.с.) электрохимического момента, в котором протекает данная реакция; z – число электронов, участвующих в элементарном акте электродной реакции.

Второй закон термодинамики имеет статистический характер. Он характеризует переход системы из менее вероятного состояния к более вероятному. Это следует из статистического характера энтропии, которая связана с термодинамической вероятностью системы уравнением Больцмана:

S = klnw

Дата добавления: 2018-02-15; просмотров: 5695; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 4 5 6 7 8910 11 12 13 Следующая ⇒

Мы поможем в написании ваших работ!