Глава 1. Предмет и метод статистики промышленности. (обьект, предмет, задачи статистики промышленности, метод статистики промышленности)
План курсовой работы.
Введение. стр.3-4
Глава 1. Предмет и метод статистики
Промышленности. (обьект, предмет,
Задачи статистики промышленности,
Метод статистики промышленности). стр.5
Глава 2. Экономическая характеристика
Машиностроения вологодской области. стр.6
Состояние и развитие отрасли
Машиностроения в Вологодской области. стр.6-8
Основные машиностроительные предприятия
Вологодской области. стр.8-10
Глава 3. Анализ тенденций и
Закономерностей развития машиностроения
Вологодской области. стр.11
Группировка предприятий по удельному
Весу в кредиторской задолженности расчётов с
Персоналом организации по оплате труда. стр.11-14
Промежуточная аналитическая группировка.
Типическая группировка предприятий
Машиностроения. стр.14-17
Комбинационная группировка по двум признакам. стр.17-22
|
|
|
Корреляционно-регрессионный анализ
Влияния факторов на финансовые результаты. стр.22-31
Индексный анализ финансовых результатов. стр.31-32
Заключение.. стр.33
Список литературы.
Введение Статистика промышленности изучает количественную сторону массовых явлений и процессов, происходящих в промышленности, неразрывной связи с их качественной стороной. Она исследует количественное выражение закономерностей промышленного производства в конкретных условиях места и времени. Эти закономерности могут быть связаны с развитием явлений, изменением структуры явлений, зависимостью одних явлений от изменения других и проявляются они только в совокупностях, свободных от влияния случайных факторов. Таким образом, изучая массовые явления и процессы, статистика промышленности выступает в качестве обобщающего учета в отличие от бухгалтерского и оперативного, предметом изучения которых служит каждый единичный факт производственной и хозяйственной деятельности отдельного предприятия. Но это не означает, что статистика не связана с другими видами учета. Напротив, все они составляют единую систему учета и статистики Статистика промышленности вскрывает и появление новых, прогрессивных явлений и процессов, которые в будущем становятся массовыми, например переход промышленных предприятий на новый порядок планирования и экономического стимулирования, образование новых производственных объединений и т.д. Статистика промышленности представляет различным министерствам и хозяйственным органам экономико-статистическую информацию о ходе выполнения государственных планов развития промышленности. Направления, темпы развития промышленности, намечаемые в планах, находят конкретное выражение в определенной системе показателей. Статистика промышленности должна, прежде всего, организовывать статистический учет, за ходом выполнения плановых заданий начиная от предприятий, производственных объединений и кончая промышленностью в целом. Обрабатывая полученные данные, статистика исчисляет показатели, характеризующие состояние промышленности за истекший период и тем самым дает исходные данные для построения плана на будущий период. Однако она не только регистрирует достигнутый уровень производства, но и анализирует выполнение планов, сигнализируя о возникновении частичных диспропорций, вскрывая внутрипромышленные резервы, и тем самым участвует в выполнении планов. Эта аналитическая задача статистики с каждым годом приобретает все большее значение. Таким образом, задачи статистики промышленности в основном определяются задачами планирования и управления этой отраслью. С первой задачей статистики промышленности тесно связана и вторая задача – разработка и анализ научно обоснованной развернутой системы статистических показателей, необходимой для всестороннего научного исследования экономики российской промышленности. Кроме того, задачами статистики промышленности являются: выявление результатов работы промышленности в целом и на отдельных ее участках, оценка степени выполнения плана, определение роли отдельных факторов, обусловивших достигнутые результаты, выявление внутрипромышленных резервов для дальнейшего увеличения выпуска продукции. Также важной задачей статистики является обеспечение достоверности и своевременности представления статистических данных.
|
|
|
|
|
|
|
|
|
Глава 1. Предмет и метод статистики промышленности. (обьект, предмет, задачи статистики промышленности, метод статистики промышленности)
Статистика промышленности, как и любая самостоятельная наука, имеет свой предмет, использует методы и приемы исследования. Она относится к экономическим наукам. Действия и проявления экономических законов в области промышленности изучают многие экономические науки: политическая экономия, экономика промышленности, планирование, бухгалтерский учет и др. При общности объекта изучения статистика промышленности отличается от других наук своим предметом. Предмет статистики промышленности -- количественная сторона массовых явлений и процессов, представляющих факторы и результат промышленного производства в конкретных условиях места и времени. Количественная определенность статистических категорий и закономерностей неразрывно связана с их качественным своеобразием, что является главной особенностью статистической методологии. Статистика промышленности изучает свой предмет, используя методы и приемы исследования, разрабатываемые общей теорией статистики. Эти методы применяются в определенной последовательности. На первом этапе применяется метод статистического наблюдения (сбор первичных данных), на втором - метод сводки и группировки результатов наблюдения (первичный анализ данных), на третьем -методы построения и анализа статистических показателей (методы сравнения, средних величин, индексный, корреляционный, регрессионный, факторного анализа и др.). Метод исследования сближает статистику промышленности со всеми отраслями статистической науки (статистика капитального строительства, статистика сельского хозяйства и др.), но отличает от других экономических наук (экономика, планирование, бухгалтерский учет и др.), объектом исследования, которых является промышленность. В то же время статистику промышленности от других отраслевых статистических наук отличает объект исследования - промышленность.
Методы анализа
Одна из важнейших черт статистических показателей, как объективных характеристик общественных явлений, состоит в их тесной взаимосвязи и взаимообусловленности. Статистика принята, вскрывать эти связи и количественно их охарактеризовать. Корреляционная, статистическая связь это неполная связь между признаками, которая проявляется при большом числе наблюдений. Используя метод корреляции, можно решить следующие задачи:
-определить среднее изменение результативного признака под влиянием одного или нескольких факторов;
-охарактеризовать меру зависимости между результативным признаком и одним из факторов при среднем значении других;
-установить меру относительного изменения признака на единицу относительного изменения фактора или факторов;
-определить меру тесноты связи результативного признака;
-подвергнуть анализу общий объём вариации результативного признака и определить роль каждого фактора в этом варьировании;
-статистически оценить показатели корреляционной связи, полученные по выборочным данным.
Для приведения корреляционно - регрессионного анализа необходимо составить систему показателей. Говоря о корреляционном отношении как о показателе измерения тесноты зависимости, следует отличать от эмпирического корреляционного отношения – теоретическое.
Теоретическое корреляционное отношение η представляет собой относительную величину, получающуюся в результате сравнения среднего квадратического отклонения выравненных значений результативного признака δ, то есть рассчитанных по уравнению регрессии, со средним квадратическим отношением эмпирических (фактических) значений результативности признака σ:
 ,где
,где  ;
;  .
.

Изменение значения η объясняется влиянием факторного признака. В основе расчёта корреляционного отношения лежит правило сложения дисперсий, то есть  , где
, где  - отражает вариацию у за счёт всех остальных факторов, кроме х , то есть являются остаточной дисперсией:
- отражает вариацию у за счёт всех остальных факторов, кроме х , то есть являются остаточной дисперсией:


Тогда формула теоретического корреляционного отношения примет вид:

Подкоренное выражение корреляционного выражения представляет собой коэффициент детерминации (мера определенности, причинности) Коэффициент детерминации показывает долю вариации результативного признака под влиянием вариации признака-фактора. Теоретическое корреляционное выражение применяется для измерения тесноты связи при линейной и криволинейной зависимостях между результативным и факторным признаком. Как видно из вышеприведенных формул корреляционное отношение может находиться от 0 до 1. Чем ближе корреляционное отношение к 1, тем связь между признаками теснее. Теоретическое корреляционное отношение применительно к моему анализу я рассчитаю двумя способами:


Полученное значение теоретического корреляционного отношения свидетельствует о возможном наличии среднестатистической связи между рассматриваемыми признаками. Коэффициент детерминации равен 0,62. Отсюда я заключаю, что 62% общей вариации работающих активов изучаемых банков обусловлено вариацией фактора – капитала банков (а 38% общей вариации нельзя объяснить изменением размера капитала). Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи – линейный коэффициент корреляции:

где n – число наблюдений. Для практических вычислений при малом числе наблюдений (n≤20ч30) линейный коэффициент корреляции удобнее исчислять по следующей формуле:

Значение линейного коэффициента корреляции важно для исследования социально-экономических явлений и процессов, распределение которых близко к нормальному. Он принимает значения в интервале: -1≤ r≤1. Отрицательные значения указывают на обратную связь, положительные – на прямую. При r = 0 линейная связь отсутствует. Чем ближе коэффициент корреляции по абсолютной величине к единице, тем теснее связь между признаками. И, наконец, при r=±1 – связь функциональная. Используя данные табл. 1 я рассчитываем линейный коэффициент корреляции r. Но чтобы использовать формулу для линейного коэффициента корреляции рассчитаем дисперсию результативного признака σy:


Квадрат линейного коэффициента корреляции r2 называется линейным коэффициентом детерминации. Из определения коэффициента детерминации очевидно, что его числовое значение всегда заключено в пределах от 0 до 1, то есть 0 ≤ r2 ≤ 1. Степень тесноты связи полностью соответствует теоретическому корреляционному отношению, которое является более универсальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции. Факт совпадений и несовпадений значений теоретического корреляционного отношения η и линейного коэффициента корреляции r используется для оценки формы связи. Выше отмечалось, что посредством теоретического корреляционного отношения измеряется теснота связи любой формы, а с помощью линейного коэффициента корреляции – только прямолинейной. Следовательно, значения η и r совпадают только при наличии прямолинейной связи. Для оценки значимости коэффициента корреляции r используют t-критерий Стьюдента, который применяется при t-распределении, отличном от нормального. Индексный анализ . Индексами в статистике называют сложные относительные показатели, характеризующие среднее изменение явления, состоящего из непосредственно несоизмеримых элементов Применение индексного анализа поможет сравнить и проанализировать показатели двух типических групп, то есть высшей и низшей.
Различают два основных вида индексов:
простые (частные, индивидуальные);
аналитические (общие, агрегатные).
В первом случае исследуемый признак принимается без учета связи этого признака с остальными признаками исследуемых экономических явлений. Такие индексы могут быть представлены следующей формулой:

 и
и  — соответственно сравниваемые состояния какого-либо признака
— соответственно сравниваемые состояния какого-либо признака
Во втором случае изучаемый признак используется не изолированно, а в его взаимосвязи с другими признаками.
Поэтому любой аналитический индекс состоит из двух элементов:
индексируемый признак  , то есть тот признак, изменение которого подвергается изучению;
, то есть тот признак, изменение которого подвергается изучению;
весовой признак  .
.
С помощью весовых признаков исследуются изменения экономических явлений, составляющие элементы которых являются несоизмеримыми. Следует иметь в виду, что простые и аналитические индексы взаимно дополняют друг друга. Аналитические индексы могут быть представлены следующим образом:
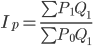 или
или 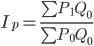
где  и
и  — весовые признаки.
— весовые признаки.
Дата добавления: 2018-02-15; просмотров: 1104; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
