Метод экспоненциальногосглаживания
При расчете прогноза методом экспоненциального сглаживания учиты- ваются отклонения предыдущего прогноза от реального показателя, а сам расчет проводится по следующей формуле:
fk=fk-1+β(xk-1–fk-1), (2.8)
где β – постоянная сглаживания (0 <β< 1). Коэффициент β обычно вы- бирают методом проб и ошибок с учетом практической деятельности.
Допустим, что на первый день работы в цехе прогноз дефектов был ра- вен 8. Тогда прогноз по каждому следующему дню от предшествующего можно сосчитать по формуле (2.8). Результаты расчета сводим в табл.2.9:
Таблица 2.9
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| x | 10 | 6 | 5 | 11 | 9 | 8 | 7 | - |
| f | 8 | 8,4 | 7,9 | 7,3 | 8,1 | 8,3 | 8,2 | 7,9 |
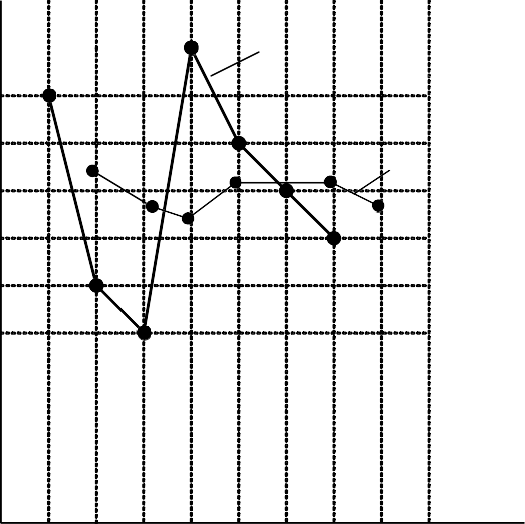
Отразим полученные результаты и на графике (рис. 2.9). Как видно из графика прогнозируемый тренд более сглажен, чем на рис. 2.8.
29
 x, f
x, f
х
10
8 f
6
4
2
1 2 3 4 5 6 7 8 9 t
Рис. 2. 9. График временного ряда (х) и прогноз (f)
по методу экспоненционального сглаживания
Метод проецированиятренда
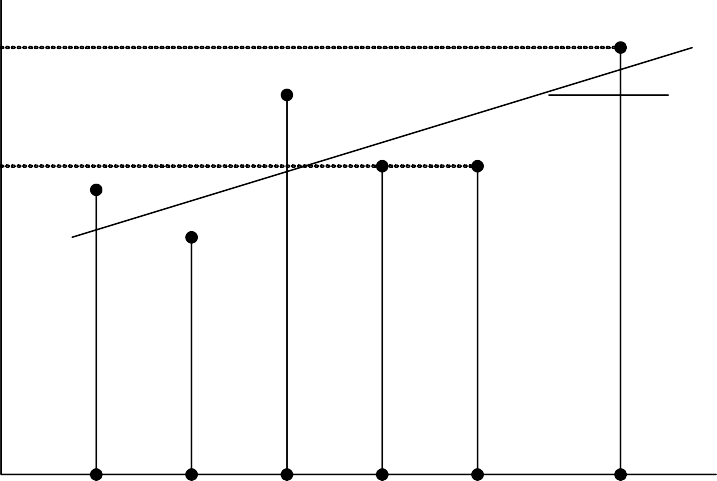
Основной идеей этого метода является построение прямой, которая «в среднем» наименее уклоняется от массива точек (t, x) заданного временного ряда (рис. 2.10), описываемого уравнением
x = аt+в, (2.9)
где а, в – постоянные коэффициенты.
Расчет коэффициентов а и в ведется по методу наименьших квадратов.
|
|
|
Т.е., решается система уравнений
n n
a×åti+вn=åxi,
| n n n |
 х хn
х хn
а
хi
t1 t2 t3 ti tn t
Рис. 2.10. Регрессионная тенденция тренда (а)
30
Эта система имеет единственное решение.
Допустим, что массив данных (t, x), принятый ранее в пункте 2.3.1, со- храняется. Для расчета коэффициентов заполним таблицу расчетов (табл.2.10).
Таблица 2.10
| ti | xi | ti · xi | ti² |
| 1 | 10 | 10 | 1 |
| 2 | 6 | 12 | 4 |
| 3 | 5 | 15 | 9 |
| 4 | 11 | 44 | 16 |
| 5 | 9 | 45 | 25 |
| 6 | 8 | 48 | 36 |
| 7 | 7 | 49 | 49 |
| Σ= 28 | Σ= 56 | Σ= 233 | Σ= 140 |
Решениеуравнений
28а + 7в = 56,
140а + 28в = 233
даст значение постоянных коэффициентов а = -0,04, в = 8,14.
Таким образом, уравнение (2.9), позволяющее дать прогноз количества дефектов в цехе на любой момент времени, принадлежащий динамическому ряду, является уравнением регрессии и имеет вид
x = -0,04t + 8,14.
Так, например, на восьмой день производства прогноз числа дефектных изделий составит
f8 = -0,04·8 + 8,14 = 7,82.
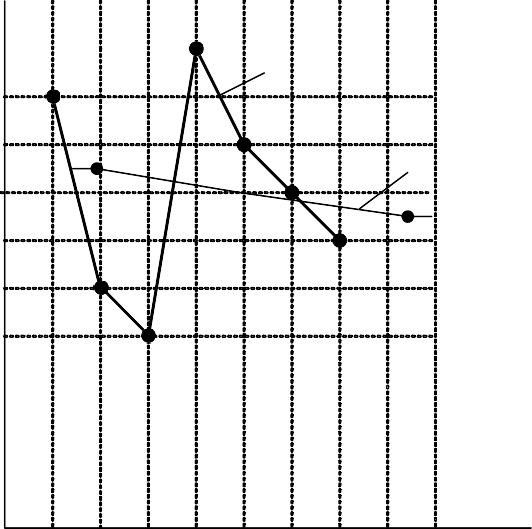
Отразим массив реальных показателей и прогноз на графике (рис. 2.11).
 x, f
x, f
х
10
8 f
|
|
|
6
4
2
1 2 3 4 5 6 7 8 9 t
Рис. 2. 11. График временного ряда (х) и прогноз (f)
по методу проецирования тренда
Следует отметить, что приведенные методы не исчерпывают многообра- зие методов анализа временных рядов.
Казуальные методыпрогнозирования
Казуальные методы используются для долгосрочных и среднесрочных прогнозов. Отметим три разновидности казуального метода (рис. 2.12):
- многомерные регрессионные методы (модели). Устанавливают рег- рессионную зависимость между величинами (факторами), влияющими на прогноз,
- эконометрические методы. Дают количественное описание законо- мерностей и взаимосвязей между объектами (чаще всего экономическими) и процессами (типичная модель состоит из тысячуравнений),
-
| Казуальные методы |
| Компьютерная имитация |
| Эконометрические модели |
| Многомерные регрессионные модели |
компьютерная имитация. Имитационные модели – это как бы проме- жуточные звенья между реальностью и обычными математическими моделя- ми. Численные решения на компьютере позволяют значительно улучшить точность аналитических прогнозов.
Рис. 2.12. Классификация казуальных методовпрогнозирования
|
|
|
Дата добавления: 2018-02-15; просмотров: 461; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
