Контрольная карта числа дефектных единиц продукции .(np – карта)
Контрольная карта числа дефектных единиц продукции (np–карта) отображает результаты регистрации доли изделий в контролируемой группе, которые «не соответствуют», отличаются от прочих или являются бракованными.
Размер выборки должен быть таким, чтобы из результатов опыта можно было ожидать появления в ней нескольких несоответствующих изделий, а частота осуществления выборки и продолжительность времени, в течение которого устанавливаются характеристики процесса, должны быть достаточными для определения источников погрешностей, оказывающих влияние на рассматриваемый процесс.
Каждое изделие должно либо соответствовать, либо не соответствовать техническим условиям, независимо от того, сколько недостатков у него обнаружено.
Таким образом, для описания соответствующего процесса наиболее применим биномиальный закон, для которого основными параметрами являются:
· np - число бракованных изделий, найденных в выборке;
· 
- стандартное отклонение.
При этом 
является средним числом бракованных изделий, найденных при первоначальном исследовании статистической выборки, а стандартное отклонение, как всегда, определяется корнем квадратным из дисперсии и равно 
.
Для построения данной формы контрольной карты необходимо:
· установить осевую линию на уровне среднего числа бракованных изделий ;
· установить предельные отклонения (±3s от среднего уровня): 
|
|
|
Контрольная карта
Числа дефектов (с-карта)
Эта карта аналогична предыдущей карте. Однако, отличается от нее тем, что здесь подсчитывается число дефектов, а не число бракованных изделий. Число недостатков верхнего предела не имеет. Каждое проконтролированное изделие может иметь различные виды дефектов или иметь многочисленные дефекты (так, например, если мы считаем число дефектов на выборочной партии яблок, то число дефектов может отличаться от числа яблок).
Поэтому для описания подобной статистики применим закон распределения Пуассона.
В этом случае среднюю линию диаграммы управляемости следует провести через точку m = c, которая соответствует среднему числу дефектов в выборке. Стандартное отклонение будет равно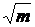 
, а верхнее и нижнее предельные отклонения устанавливаются на уровнях: 
.
Контрольные карты для средних арифметических значений и размахов: 
и R
Непрерывная переменная, характеризующая какое-либо свойство продукции, (т.е. переменная, которая может принимать любые значения, а не только дискретные) будет всегда иметь тенденцию к нормальному закону распределения, если выполняются следующие условия:
(а) каждое изделие изготавливается на одно и то же номинальное целевое значение, но при этом:
|
|
|
(б) имеется множество малых возмущений, которые не позволяют точно достигнуть этого номинального значения, причем:
· влияние каждого возмущения независимо и аддитивно;
· среднее результирующее каждого возмущения равно нулю.
Нормальное распределение с любыми значениями параметров m и s может быть стандартизовано (приведено нормальному распределению с параметрами m 0 = 0 и s 20 = 1) простым преобразованием:
Z = (x - m )/ s ,
где х - конкретное значение из распределения, которое анализируется.
Ранее мы рассматривали отдельные наблюдения, взятые из нормального распределения. Однако при построении контрольных карт мы не анализируем каждое отдельное изделие, а только их выборки.
Чем меньше объем выборки, тем более узкого размаха (разброса) значений мы вправе ожидать. Для выборок справедливы утверждения:
· если генеральная совокупность имеет нормальный закон распределения, то и распределение в выборке также будет нормальным;
· среднее значение в выборке будет таким же, что и в генеральной совокупности: 
;
· стандартное отклонение для среднего арифметического выборки будет равно стандартному отклонению для генеральной совокупности, деленному на корень квадратный из объема выборки: 
, где n - размер выборки.
|
|
|
Другим преимуществом выборок является то, что даже если генеральная совокупность не подчиняется нормальному закону распределения, то распределение в выборке является приблизительно нормальным. Поэтому в результате построения контрольной карты в предположении нормального закона распределения может быть получен верный результат даже тогда, когда генеральная совокупность не подчиняется нормальному закону распределения.
Дата добавления: 2018-02-15; просмотров: 596; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!