Параметры выборки и распределения вероятностей
Эти параметры обычно разделяют на характеристики расположения и рассеяния. Наиболее распространенном характеристикой расположения является среднее значение. Если мы возьмем некоторое число n наблюденных значений 
переменной величины x, сложим их и разделим на число наблюдений, то получим среднее значение х как среднее арифметическое,
Основной мерой рассеяния выборочных значений является среднее квадратичное отклонение S, которое вычисляется по одной из двух следующих формул:
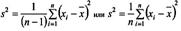
Вторая из них используется для достаточно больших n (n>10). она соответствует следующему простому правилу: 
("квадрат среднеквадратичного есть среднее квадрата величины минус квадрат среднего").
Вернемся к примеру с n - бросаниями монеты. Если при i-ом бросании выпадает орел, то переменной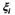 
будем присваивать значение 1, а в противоположном случае - 0. Число выпадении орла 
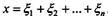В соответствии с законом статнетической устойчивости, относительное значение частоты x/n будет колебаться около значения вероятности выпадения орла р=0,5. При этом, амплитуда отклонений относительной частоты x/n от значения р уменьшается в среднем. Таким образом, при достаточно больших n можно ожидать, что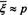 
.
Далее мы можем рассмотреть более сложную ситуацию, когда проводится N серий с n- кратными бросаниями монеты (аналог N партий в каждой из которых делается выборка объема n). Тогда мы получим серию числа "успехов" . 
при этом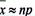 
. Действительно,
|
|
|
Величины p и np определяются точные значения уровней, вокруг которых колеблются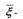 
-среднее значение числа успехов в одном испытании, и 
среднее число успехов в серии из n испытаний, причем амплитуда этих колебаний уменьшается с возрастанием объема выборки n и числа партий N для 
и 
cоответствешю. Эти теоретические значения называются математическими ожиданиями величин 
. Математическое ожидание обычно обозначается буквами М или 
В таком же смысле в среднеквадратичные отклонения стремятся к некоторым своим предельным значениям, которые называются стандартными отклонениями и обозначаются
греческой буквой 
. Квадрат стандартного отклонения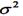 
называется дисперсией и обозначается через D. Для целочисленной случайной величины d с распределением вероятностей Р(d) математическое ожидание и дисперсия равны, соответственно.
Для единичного испытания с двумя исходами "успех" и "неудача", вероятности которых суть р и 
ожидаемое число успехов равно 
, а дисперсия 
вычисляется так 
В серии из n такого рода независимых испытании число успехов d имеет биномиальное распределение вероятностей 
, при этом d есть сумма одинаково распределенных и независимых случайных величин 
Математическое ожидание и дисперсия таких сумм выражаются простыми формулами,
|
|
|
Используя эти формулы и приведенные ваше результаты для единичного испытания, мы подучим следующие выражения для основных параметров биномиального распределения вероятностей:
Если все выборочные значения 
независимы и распределены одинаково, то математическое ожидание среднего 
совпадает с математическим ожиданием любого из слагаемых . поскольку их математические ожидания равны между собой, 
. Пусть 
есть константа (число), тогда для случайной величины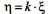 
, справедливы следующие равенства: 
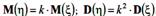. В силу последней формулы дисперсия среднего равна 
, то есть в N раз меньше дисперсии каждого отдельного слагаемого.
Соответственно, стандартное отклонение среднего 
, в 
раз меньше стандартного отклонения любого из слагаемых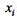 
. Сказанное выше означает, что амплитуда случайных колебаний 
около числа 
с увеличением N уменьшается как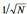 
. При больших N среднее можно использовать в качестве оценки математическою ожидания , и наоборот есть оценка X при больших N. Точно также СКО является при больших N оценкой стандартного отклонения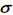 
(и наоборот).Рагмах R- что еще одна характеристика ряда выборочных значений. Размах равен разнице между наибольшим и наименьшим значениями в выборке 
|
|
|
Биноменальное распределение
Пусть имеется некое событие A. Вероятность появления события A равна p, вероятность непоявления события A равна 1 – p, иногда ее обозначают как q. Пусть n — число испытаний, m — частота появления события A в этих n испытаниях.
Известно, что суммарная вероятность всех возможных комбинаций исходов равна единице, то есть:
1 = pn + n · pn – 1 · (1 – p) + Cnn – 2 · pn – 2 · (1 – p)2 + … + Cnm · pm · (1 – p)n – m + … + (1 – p)n.
pn — вероятность того, что в n испытаниях событие A произойдет n раз;
n · pn – 1 · (1 – p) — вероятность того, что в n испытаниях событие A произойдет (n – 1) раз и не произойдет 1 раз;
Cnn – 2 · pn – 2 · (1 – p)2 — вероятность того, что в n испытаниях событие A произойдет (n – 2) раза и не произойдет 2 раза;
Pm = Cnm · pm · (1 – p)n – m — вероятность того, что в n испытаниях событие A произойдет m раз и не произойдет (n – m) раз;
(1 – p)n — вероятность того, что в n испытаниях событие A не произойдет ни разу;
— число сочетаний из n по m.
Математическое ожидание M биномиального распределения равно:
M = n · p,
где n — число испытаний, p — вероятность появления события A.
|
|
|
Среднеквадратичное отклонение σ:
σ = sqrt(n · p · (1 – p)).
Распределение Пуассона.
Распределение Пуассона — это частный случай биномиального распределения (при n >> 0 и при p –> 0 (редкие события)).
Из математики известна формула, позволяющая примерно подсчитать значение любого члена биномиального распределения:
где a = n · p — параметр Пуассона (математическое ожидание), а дисперсия равна математическому ожиданию. Приведем математические выкладки, поясняющие этот переход. Биномиальный закон распределения
Pm = Cnm · pm · (1 – p)n – m
может быть написан, если положить p = a/n, в виде
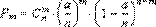
или
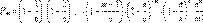
Так как p очень мало, то следует принимать во внимание только числа m, малые по сравнению с n. Произведение
весьма близко к единице. Это же относится к величине
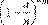
Величина
очень близка к e–a. Отсюда получаем формулу:
Дата добавления: 2018-02-15; просмотров: 370; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!