Нормальное распределение вероятности

⇐ ПредыдущаяСтр 3 из 6Следующая ⇒

Нормальное распределение выделяется своим фундаментальным значением среди остальных распределений. Ему подчиняются непрерывные случайные величины , значения которых зависит от большого числа случайных воздействий. Это в равной степени могут быть случайные ошибки эксперимента и множество случайных воздействий на технологический процесс.

Важным для практики свойством нормального закона является то, что он является хорошей аппроксимацией биномиального и пуассоновского распределений при достаточно больших и .

Распределение вероятностей для среднего значения

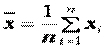
выборки обычно близко к нормальному закону даже, если отдельные выборочные значения распределены существенно иным образом.

Нормальной плотностью вероятности называется плотность, определяемая равенством

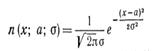
для любого значения 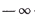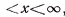, где 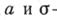—произвольные числа (параметры распределения), причем положительно.

Рис. 2.6

Нормальная плотность вероятности называется также дифференциальной функцией нормального распределения. График дифференциальной функции нормального распределения показан на рис. 2.6.

Интегральная функция нормального распределения определяется в виде

полная площадь под всей кривой выразится интегралом

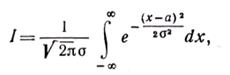
который путем замены переменного на , откуда 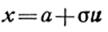и , преобразуется в интеграл

График интегральной функции распределения показан на рис. 2.7.

Из рисунка видно, что плотность нормального распределения симметрична относительно ординаты, отвечающей значению x=a

Это значение является поэтому центром группирования (математическим ожиданием) распределения.

Чаще всего, однако, рассматривая величину, подчиненную нормальному закону переходят к нормированному распределению.

Нормирование распределения, вообще говоря, заключается в переходе от величины к вспомогательной линейной функции

……

Рис. 2.7

для которой

При нормальном распределении будем иметь:

или

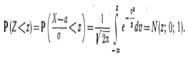
После дифференцирования получим

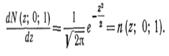
Все вопросы, связанные с нормальным распределением величины решают, переходя к вспомогательной величине , т. е. нормируя это распределение.

Нормирование распределения, как нетрудно понять, ведет просто к перенесению начала координат в центр группирования, т. е. к «центрированию», и к выражению абсциссы в долях которое, как мы дальше увидим, представляет среднеквадратическое отклонение величины т. е.

Планы выборочного контроля

Одним из важных понятий, которое используется при организации приемочного контроля, является понятие засоренности дефектными изделиями при нормальном ходе производства.

Под нормальным ходом производства понимается такое его состояние, когда основные требования технологии соблюдены.

Засоренность дефектными изделиями при нормальном ходе производства невелика, но она реально всегда существует, а в случае нарушения технологии может возрасти. Задача статистических методов контроля качества продукции состоит в том, чтобы большинство партий партий продукции, выпущенных при нормальном ходе производства - принимались, а большинство партий, выпущенных при

Рис.3.1. Кривые оперативных характеристик для планов выборочного контроля: (50,2) –кривая 1; (100,2) – кривая 2;

разлаженном ходе производства - браковались.

Для организации выборочного контроля следует задать систему правил, именуемых планом контроля, в котором указывается порядок отбора изделий для проверки и их количество достаточное для принятия решения о браковке или приемке партий в целом, или о дальнейшем продолжении контроля. Наибольшее распространение получили три типа планов выборочного контроля по альтернативным признакам.

Планы типа однократной выборки

Из партии объема N отбираются случайным образом n 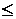N изделий, которые подвергаются проверке.

Если число обнаруженных дефектных изделий среди n элементов равно d(n) 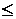c, где с - целое число, называемое приемочным числом, то партия принимается.

Если же d(n) > c, то партия бракуется.

Планы типа двукратной (многократной) выборки

Из партии объема N случайным образом отбирается n₁ элементов (первая выборка), если число обнаруженных дефектных изделий d(n₁) 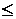c, то партия принимается, а если d(n₁) > c₂ > c₁ , то бракуется, если же c₁< d(n₁) 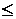c₂, то берется вторая выборка из n₂ элементов.

Если общее число обнаруженных в двух выборках дефектных элементов d(n₁+n₂) 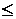c₃, то партия принимается, в противном случае - партия бракуется.

Часто используются усеченные планы типа двукратной выборки, в которых c₂= c₃.

Планы типа последовательного анализа

При использовании этих планов задаются объемы последовательных выборок n_i, где i =1,2,..., причем n₁< N ;

n₁ + n₂ < N и т. д. Кроме того, для каждой последовательной выборки задаются пары целых чисел c_i₁ и c_i₂. В начале контроля берется выборка объема n₁.

Если d(n₁) < c₁₁, то партия принимается, если d(n₁) > c₁₂ - бракуется, если же c₁₁ < d(n₁) 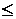c₁₂, то берется выборка объема n₂и т.д. На i-м шаге, если d(n_i) < c_i₁, то партия принимается, если d(n_i) > c_i₂ - бракуется, если c_i₁ < d(n_i) 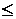c_i₂, то берется выборка объема n_i₊₁ и т.д.

Каждый из указанных выше типов обладает рядом преимуществ и недостатков.

С организационной точки зрения планы типа однократной выборки значительно проще. Здесь к тому же заранее известен объем выборки.

В планах типа двукратной выборки и последовательного анализа можно при том же среднем объеме выборки получить большую достоверность соответствия принимаемых решений с истинным положением дела. Однако здесь могут встретиться случаи, когда общий объем выборок будет чрезмерно велик. Оценка качества продукции для планов типов II и III значительно сложнее, чем для планов типа I.

Дата добавления: 2018-02-15; просмотров: 325; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 Следующая ⇒

Мы поможем в написании ваших работ!