Размещение и перестановки. Соединение и выборки. Сочетание.
Вероятность случайных событий. Операций над событиями и вероятностями.
Случайным событием (или просто событием) называется всякое явление, которое может произойти или не произойти при осуществлении определенной совокупности условий. Теория вероятностей имеет дело с такими событиями, которые имеют массовый характер. Это значит, что данная совокупность условий может быть воспроизведена неограниченное число раз. Каждое такое осуществление данной совокупности условий называют испытанием (или опытом).
Если, например, испытание состоит в бросании монеты, то выпадение герба является событием; если испытание — изготовление подшипника данного типа, то соответствие подшипника стандарту — событие; если испытание — бросание игральной кости, т. е. кубика, на гранях которого проставлены цифры (очки) от 1 до 6, to выпадение пятерки — событие.
События будем обозначать заглавными буквами латинского алфавита: A, В, С, ... .
Пусть при n испытаниях событие A появилось m раз.
Отношение m/n называется частотой (относительной частотой) события A и обозначается Р*(А)=m/n
Опыт показывает, что при многократном повторении испытаний частота Р*(А) случайного события обладает устойчивостью. Поясним это на примере.
Пусть при бросании монеты 4040 раз герб выпал 2048 раз. Частота появления герба в данной серии опытов равна Р*(А)=m/n=2048/4040=0,5069. При бросании той же монеты 12000 раз герб выпал 6019 раз. Следовательно, в этом случае частота Р*(А)=6019/12000=0,5016. Наконец, при 24000 бросаний герб появился 12012 раз с частотой Р*(А)=0,5005. Таким образом, мы видим, что при большом числе бросаний монеты частота появления герба обладает устойчивостью, т. е. мало отличается от числа 0,5. Как показывает опыт, это отклонение частоты от числа 0,5 уменьшается с увеличением числа испытаний. Наблюдаемое в этом примере свойство устойчивости частоты является общим свойством массовых случайных событий, а именно, всегда существует такое число, к которому приближается частота появления данного события, мало отличаясь от него при большом числе испытаний. Это число называется вероятностью события. Оно выражает объективную возможность появления события. Чем больше вероятность события, тем более возможным оказывается его появление. Вероятность события A будем обозначать через Р(А). В рассмотренном выше примере вероятность появления герба, очевидно, равна 0,5.
|
|
|
Событие называется достоверным, если оно в данном опыте обязательно должно произойти; наоборот, событие называется невозможным, если оно в данном опыте не может произойти.
Пусть, например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара — достоверное событие; появление белого шара — невозможное событие.
|
|
|
Если событие достоверно, то оно произойдет при каждом испытании (m=n). Поэтому частота достоверного события всегда равна единице. Наоборот, если событие невозможно, то оно ни при одном испытании не осуществится (m=0). Следовательно, частота невозможного события в любой серии испытаний равна нулю. Поэтому вероятность достоверного события равна единице, а вероятность невозможного события равна нулю.
Если событие A не является ни достоверным, ни невозможным, то его частота m/n при большом числе испытаний будет мало отличаться от некоторого числа p (где 0 < p < 1 ) — вероятности события A.
Совмещением (или произведением) двух событий A и В называется событие, состоящее в совместном наступлении как события A, так и события В. Это событие будем обозначать АВ или ВА.
Аналогично, совмещением нескольких событий, например A, В и С, называется событие D=ABC, состоящее в совместном наступлении событий A, В и С.
Объединением (или суммой) двух событий A и В называется событие С, заключающееся в том, что произойдет по крайней мере одно из событий A или В. Это событие обозначается так: С=А+В.
Объединением нескольких событий называется событие, состоящее в появлении по крайней мере одного из них. Запись D=A+B+C означает, что событие D есть объединение событий A, В и С.
|
|
|
Два события A и В называются несовместными, если наступление события A исключает наступление события В. Отсюда следует, что если события A и В несовместны, то событие AB — невозможное.
Размещение и перестановки. Соединение и выборки. Сочетание.
Размещения.
Размещениями из 
элементов по 
называются соединения, которые можно образовать из элементов, собирая в каждое соединение по элементов, при этом соединения могут отличаться друг от друга как самими элементами, так и порядком их расположения.
Например, из 3 элементов (a,b,c) по 2 можно образовать следующие размещения:
ab, ac, ba, bc, ca, cb.
Число всех возможных размещений, которые можно образовать из элементов по , обозначается символом 
и вычисляется по формуле:
,
(всего k множителей).
Пример: 
Перестановки.
Перестановками из n элементов называются соединения, каждое из которых содержит все n элементов, отличающихся поэтому друг от друга только порядком расположения элементов.
Например, из 3 элементов (a,b,c) можно образовать следующие перестановки:
|
|
|
abc, bac, cab, acb, bca, cba.
Число всех возможных перестановок, которые можно образовать из n элементов, обозначается символом 
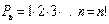
(Произведение n первых целых чисел обозначается символом “n!” и читается “n факториал”)
Пример: 
Соединения и выборки
Процедура построения размещений называется еще выбор без возвращений, при этом каждое из размещений называют упорядоченной выборкой объема m. В другом случае, при выборе с возвращением любой элемент, извлеченный для формирования выборки из исходной совокупности (генеральная совокупность), заменяется эквивалентным и происходит восстановление исходного состава генеральной совокупности.
Таким образом, в конкретной выборке каждый элемент может встречаться несколько раз.
Все возможные выборки с возвращением, которые можно сформировать из элементов трех типов a, b и c по 2, будут такие (сравни с предыдущим случаем):
aa, ab, ac, ba, bb, bc, ca, cb, cc;
Для формирования всех таких соединений по 2 надо записать строку исходных элементов дважды
a, b, c…
a, b, c…
и каждый элемент первой строки последовательно объединять со всеми элементами второй строки.
Если полное число элементов есть n, то число возможных соединений по 2 равно 
.
Итак, если объем выборок равен m, то необходимо записать m строк и, следовательно, количество упорядоченных выборок с возвращением будет равно 
.
В комбинаторике стремятся к формальной аналогии в записи близких по своему смыслу величин. Поэтому число выборок без возвращений (число размещений) часто записывают, как 
. Последнюю величину полагают по определению равной
и называют убывающий m-факториал.
Очевидно, что при m=n справедливо следующее равенство: 
Сочетания.
Сочетаниями из n элементов по k называются соединения, которые можно образовать из n элементов, собирая в каждое соединение k элементов; при этом соединения отличаются друг от друга только самими элементами (различие порядка их расположения во внимание не принимается).
Например, из 3 элементов (a,b,c) по 2 можно образовать следующие сочетания:
ab, ac, bc.
Число всех возможных сочетаний, которые можно образовать из n элементов по k, обозначается символом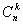 
:
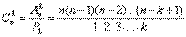
(В числителе и знаменателе по k множителей).
Пример: 
Полезные формулы:
Например: 
Дата добавления: 2018-02-15; просмотров: 461; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!