Формула Верещагина для определения перемещений и условие жесткости.
Вычисление интеграла Мора целесообразно вести по правилу, предложенному А. Н. Верещагиным в 1925 г. для прямолинейных брусьев.
Уравнения изгибающих моментов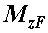 
и 
, входящие в формулу интеграла Мора, - это некоторые функции от х: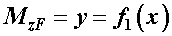 
, 
, а графики этих функций - эпюры 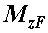и (рисунок 1) на некотором участке балки. Причем если первая функция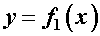 
может быть и нелинейной, то вторая 
, выражающая изгибающий момент от единичной силы (или единичного момента), обязательно линейная. Поэтому ее можно представить уравнением прямой с угловым коэффициентом, т. е.
.
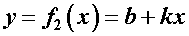Следовательно, вычисление интеграла 
можно заменить вычислением интеграла
.
Раскрыв скобки под интегралом в правой части равенства, получим
|
| Рисунок 1 |
Произведение 
есть не что иное, как заштрихованная на рисунке 1 элементарная площадка эпюры 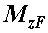. Значит, первый интеграл в правой части равенства выражает площадь эпюры 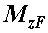в интервале от х=0 до x=l, а второй интеграл - статический момент этой же площади относительно оси у, который, как известно из формулы, выражается произведением площади на координату 
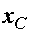ее центра тяжести С. Если площадь эпюры 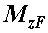обозначить буквой 
, то равенство примет вид
,
где 
, т. е. ордината эпюры под центром тяжестиС эпюры 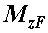. Следовательно, в окончательном виде
.
Теперь формула интеграла Мора может быть записана так:
.
Таким образом, правило Верещагина состоит в том, что интеграл Мора, составленный для каждого из участков нагружения балки, равен произведению площади нелинейной эпюры изгибающих моментов 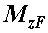на ординату 
эпюры изгибающего момента , соответствующую положению центра тяжести площади .
Вычисление интеграла Мора по правилу Верещагина обычно называют методом перемножения эпюр. Эпюра 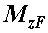называется грузовой эпюрой, а эпюра - единичной.
При перемножении эпюр необходимо иметь в виду следующее: произведение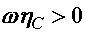 
, если площадь и ордината расположены по одну сторону от базовых линий;
при расположении и по разные стороны от базовых линий 
;
если в пределах данного участка грузовая эпюра линейна, то безразлично, умножается ли площадь грузовой эпюры на ординату единичной или, наоборот, площадь единичной эпюры на ординату грузовой;
поетроенные эпюры 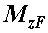и не штрихуют.
|
|
|
Понятие о сложном сопротивлении. Виды сложного сопротивления.
Сложным сопротивлением называются виды нагружения, при которых в поперечных сечениях одновременно действуют несколько внутренних силовых факторов.
Наиболее часто в расчетной практике встречаются следующие виды сложного сопротивления:
- косой изгиб;
-внецентренное растяжение;
-изгиб с кручением.
При расчете сложного сопротивления используется принцип независимости действия сил. Сложный вид нагружения представляется как система простых видов нагружения действующих независимо друг от друга. Решение при сложном сопротивлении получается в результате сложения решений полученных при простых видах нагружения.
|
|
|
Дата добавления: 2018-02-15; просмотров: 930; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!