Дифференциальные уравнения в полных дифференциалах.
Определение. Если в уравнении M(x,y)dx+N(x,y)dy=0 (9.1) левая часть есть полный дифференциал некоторой функции U(x,y), то оно называется уравнением в полных дифференциалах. Это уравнение можно переписать в виде du(x,y)=0, следовательно, его общий интеграл есть u(x,y)=c.
Например, уравнение xdy+ydx=0 есть уравнение в полных дифференциалах, так как его можно переписать в виде d(xy)=0. Общим интегралом будет xy=c.
Теорема. Предположим, что функции M и N определены и непрерывны в некоторой односвязной области D и имеют в ней непрерывные частные производные соответственно по y и по x. Тогда, для того, чтобы уравнение (9.1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось тождество 
(9.2).
Доказательство.
Доказательство необходимости этого условия очевидно. Поэтому докажем достаточность условия (9.2). Покажем, что может быть найдена такая функция u(x,y), что 
и 
.
Действительно, поскольку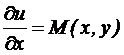 
,то
(9.3) , где 
- произвольная дифференцируемая функция. Продифференцируем (9.3) по y:
. Но , следовательно, 
.
Положим 
и тогда 
.
Итак, построена функция 
, для которой 
, а 
.
Рассмотрим пример.
Пример. Найти общий интеграл уравнения: 
.
Решение. Здесь 
Тогда 
. Следовательно, заданное дифференциальное уравнение 1-го порядка является уравнением в полных дифференциалах, т.е. существует такая функция u(x,y), частные производные которой соответственно по x и y равны M(x,y) и N(x,y):
|
|
|
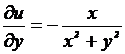. Интегрируем первое из двух соотношений по x:
, 
.
Теперь продифференцируем u(x,y) по y и приравняем полученное в результате выражение выписанной выше частной производной 
:
.
Откуда 
и 
. Следовательно, общим интегралом заданного уравнения является: 
.
Интегрирующий множитель.
Если уравнение M(x,y)dx + N(x,y)dy = 0 не является уравнением в полных дифференциалах и существует функция µ = µ(x,y), такая что после умножения на нее обеих частей уравнения получается уравнение
µ(Mdx + Ndy) = 0 в полных дифференциалах, т. е. µ(Mdx + Ndy)du, то функция µ(x,y) называется интегрирующим множителем уравнения. В случае, когда уравнение уже есть уравнение в полных дифференциалах, полагают µ = 1.
Если найден интегрирующий множитель µ, то интегрирование данного уравнения сводится к умножению обеих его частей на µ и нахождению общего интеграла полученного уравнения в полных дифференциалах.
Если µ есть непрерывно дифференцируемая функция от x и y, то 
.
Отсюда следует, что интегрирующий множитель µ удовлетворяет следующему уравнению с частными производными 1-го порядка:
(10.1).
Если заранее известно, что µ= µ(ω), где ω – заданная функция от x и y, то уравнение (10.1) сводится к обыкновенному (и притом линейному) уравнению с неизвестной функцией µ от независимой переменной ω:
|
|
|
(10.2),
где 
, т. е. дробь является функцией только от ω.
Решая уравнение (10.2), находим интегрирующий множитель
, с = 1.
В частности уравнение M(x,y)dx + N(x,y)dy = 0 имеет интегрирующий множитель, зависящий только от x (ω = x) или только от y (ω = y), если выполнены соответственно следующие условия:
, 
или
, 
.
Дата добавления: 2018-02-15; просмотров: 429; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!