Дифференциальные уравнения 1-го порядка с разделяющимися переменными.
Определение. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида 
(3.1)
или уравнение вида 
(3.2)
Для того, чтобы в уравнении (3.1) разделить переменные, т.е. привести это уравнение к так называемому уравнению с разделенными переменными, произвести следующие действия:
;
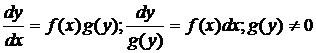
Теперь надо решить уравнение g(y)= 0. Если оно имеет вещественное решение y=a, то y=a тоже будет решением уравнения (3.1).
Уравнение (3.2) приводится к уравнению с разделенными переменными делением на произведение 
:
, что позволяет получить общий интеграл уравнения (3.2): 
. (3.3)
Интегральные кривые (3.3) будут дополнены решениями 
, если такие решения существуют.
Пример.
Решить уравнение: 
.
Решение.
Разделяем переменные:
.
Интегрируя, получаем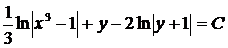 
Далее из уравнений 
и 
находим x=1, y=-1. Эти решения – частные решения.
Однородные дифференциальные уравнения 1-го порядка.
Определение 1. Уравнение 1-го порядка 
называется однородным, если для его правой части при любых 
справедливо соотношение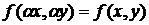 
, называемое условием однородности функции двух переменных нулевого измерения.
Пример 1. Показать, что функция 
- однородная нулевого измерения.
Решение. 
,
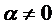что и требовалось доказать.
Теорема. Любая функция 
- однородна и, наоборот, любая однородная функция 
нулевого измерения приводится к виду 
.
Доказательство.
Первое утверждение теоремы очевидно, т.к. 
. Докажем второе утверждение. Положим 
, тогда для однородной функции 
, что и требовалось доказать.
|
|
|
Определение 2. Уравнение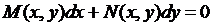 
(4.1)
в котором M и N – однородные функции одной и той же степени, т.е. обладают свойством 
при всех 
, называется однородным.
Очевидно, что это уравнение всегда может быть приведено к виду 
(4.2) , хотя для его решения можно этого и не делать.
Однородное уравнение приводится к уравнению с разделяющимися переменными с помощью замены искомой функции y по формуле y=zx, где z(x) – новая искомая функция. Выполнив эту подстановку в уравнении (4.2), получим: 
или 
или 
.
Интегрируя, получаем общий интеграл уравнения относительно функции z(x) 
, который после повторной замены 
дает общий интеграл исходного уравнения. Кроме того, если 
- корни уравнения 
, то функции 
- решения однородного заданного уравнения. Если же 
, то уравнение (4.2) принимает вид
и становится уравнением с разделяющимися переменными. Его решениями являются полупрямые: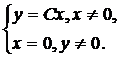 
.
Замечание. Иногда целесообразно вместо указанной выше подстановки использовать подстановку x=zy.
Дифференциальные уравнения, приводящиеся к однородным.
Рассмотрим уравнение вида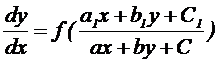 
. (5.1)
|
|
|
Если 
, то это уравнение с помощью подстановки 
, где 
и 
- новые переменные, а 
и 
- некоторые постоянные числа, определяемые из системы 
Приводится к однородному уравнению 
Если 
, то уравнение (5.1) принимает вид
.
Полагая z=ax+by, приходим к уравнению, не содержащему независимой переменной.
Рассмотрим примеры.
Пример 1.
Проинтегрировать уравнение 
и выделить интегральную кривую, проходящую через точки: а) (2;2); б) (1;-1).
Решение.
Положим y=zx. Тогда dy=xdz+zdx и
.
Сократим на 
и соберем члены при dx и dz:
.
Разделим переменные: 
.
Интегрируя, получим 
;
или 
, 
.
Заменив здесь z на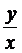 
, получим общий интеграл заданного уравнения в виде (5.2) 
или 
.
Это семейство окружностей 
, центры которых лежат на прямой y = x и которые в начале координат касаются прямой y + x = 0. Эта прямая y = -x в свою очередь частное решение уравнения.
Теперь режим задачи Коши:
А) полагая в общем интеграле x=2, y=2, находим С=2, поэтому искомым решением будет 
.
Б) ни одна из окружностей (5.2) не проходит через точку (1;-1). Зато полупрямая y = -x, 
проходит через точку и дает искомое решение.
Пример 2. Решить уравнение: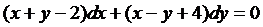 
.
Решение.
Уравнение является частным случаем уравнения (5.1).
Определитель 
в данном примере 
, поэтому надо решить следующую систему 
|
|
|
Решая, получим, что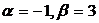 
. Выполняя в заданном уравнении подстановку 
, получаем однородное уравнение 
. Интегрируя его при помощи подстановки 
, находим 
.
Возвращаясь к старым переменным x и y по формулам 
, имеем 
.
Дата добавления: 2018-02-15; просмотров: 454; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!