Обобщенное однородное уравнение.

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

Уравнение M(x,y)dx+N(x,y)dy=0 называется обобщенным однородным, если удается подобрать такое число k, что левая часть этого уравнения становится однородной функцией некоторой степени m относительно x, y, dx и dy при условии, что x считается величиной первого измерения, y – k‑го измерения, dx и dy – соответственно нулевого и (k-1)-го измерений. Например, таким будет уравнение 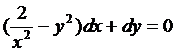. (6.1)

Действительно при сделанном предположении относительно измерений

x, y, dx и dy члены левой части и dy будут иметь соответственно измерения -2, 2k и k-1. Приравнивая их, получаем условие, которому должно удовлетворять искомое число k: -2 = 2k = k-1. Это условие выполняется при k = -1 (при таком k все члены левой части рассматриваемого уравнения будут иметь измерение -2). Следовательно, уравнение (6.1) является обобщенным однородным.

Обобщенное однородное уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки 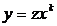, где z – новая неизвестная функция. Проинтегрируем указанным методом уравнение (6.1). Так как k = -1, то , после чего получаем уравнение .

Интегрируя его, находим , откуда . Это общее решение уравнения (6.1).

Линейные дифференциальные уравнения 1-го порядка.

Линейным уравнением 1-го порядка называется уравнение, линейное относительно искомой функции и ее производной. Оно имеет вид:

, (7.1)

где P(x) и Q(x) – заданные непрерывные функции от x. Если функция , то уравнение (7.1) имеет вид: (7.2)

и называется линейным однородным уравнением, в противном случае оно называется линейным неоднородным уравнением.

Линейное однородное дифференциальное уравнение (7.2) является уравнением с разделяющимися переменными:

(7.3)

Выражение (7.3) есть общее решение уравнения (7.2). Чтобы найти общее решение уравнения (7.1), в котором функция P(x) обозначает ту же функцию, что и в уравнении (7.2), применим прием, называемый методом вариации произвольной постоянной и состоящий в следующем: постараемся подобрать функцию С=С(x) так, чтобы общее решение линейного однородного уравнения (7.2) являлось бы решением неоднородного линейного уравнения (7.1). Тогда для производной функции (7.3) получим:

Подставляя найденную производную в уравнение (7.1), будем иметь:

или .

Откуда , где 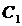- произвольная постоянная. В результате общее решение неоднородного линейного уравнения (7.1) будет (7.4)

Первое слагаемое в этой формуле представляет общее решение (7.3) линейного однородного дифференциального уравнения (7.2), а второе слагаемое формулы (7.4) есть частное решение линейного неоднородного уравнения (7.1), полученное из общего (7.4) при . Этот важный вывод выделим в виде теоремы.

Теорема. Если известно одно частное решение линейного неоднородного дифференциального уравнения , то все остальные решения имеют вид , где - общее решение соответствующего линейного однородного дифференциального уравнения.

Однако надо отметить, что для решения линейного неоднородного дифференциального уравнения 1-го порядка (7.1) чаще применяется другой метод, иногда называемый методом Бернулли. Будем искать решение уравнения (7.1) в виде . Тогда . Подставим найденную производную в исходное уравнение: .

Объединим, например, второе и третье слагаемые последнего выражения и вынесем функцию u(x) за скобку: (7.5)

Потребуем обращения в нуль круглой скобки: .

Решим это уравнение, полагая произвольную постоянную C равной нулю: . С найденной функцией v(x) вернемся в уравнение (7.5): .

Решая его, получим: .

Следовательно, общее решение уравнения (7.1) имеет вид:

Уравнение Бернулли.

Определение.

Дифференциальное уравнение вида , где , называется уравнением Бернулли.

Предполагая, что , разделим обе части уравнения Бернулли на . В результате получим: (8.1)

Введем новую функцию . Тогда . Домножим уравнение (8.1) на и перейдем в нем к функции z(x): , т.е. для функции z(x) получили линейное неоднородное уравнение 1-го порядка. Это уравнение решается методами, разобранными в предыдущем параграфе. Подставим в его общее решение вместо z(x) выражение , получим общий интеграл уравнения Бернулли, который легко разрешается относительно y. При 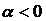добавляется решение y(x)=0. Уравнение Бернулли можно также решать, не делая перехода к линейному уравнению путем подстановки , а применяя метод Бернулли, подробно разобранный в § 7. Рассмотрим применение этого способа для решения уравнения Бернулли на конкретном примере.

Пример. Найти общее решение уравнения: (8.2)

Решение.

Уравнение (8.2) является уравнением Бернулли, причем .

Будем искать решение уравнения в виде .

Тогда .

В левой части последнего уравнения сгруппируем второе и третье слагаемые, которые содержат функцию u(x), и потребуем, чтобы . Откуда . Тогда для функции u(x) будем иметь следующее уравнение:

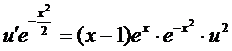или ,

которое является уравнением с разделяющимися переменными для функции u(x). Решим его ,

Следовательно, общее решение данного уравнения имеет вид: , y(x)=0.

Дата добавления: 2018-02-15; просмотров: 585; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 Следующая ⇒

Мы поможем в написании ваших работ!