Дифференциальные зависимости между ВСФ и между интенсивностью внешних распределения нагрузок и ВСФ.
Интегральные зависимости между s и tи внутренними силовыми факторами
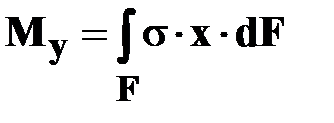
| y |
| x |
| s |
| z |
| tyz |
| tzx |
| t |
| r |
|
Рис. 3.3Связь между напряжениями и внутренними усилиями
Правило построения и контроля построения эпюр ВСФ.
В различных сечениях одного и того же бруса внутренние силовые факторы различны. Для расчета конструкций на прочность весьма важно знать как величину внутренних силовых факторов, так и характер их изменения по длине бруса, что устанавливается по эпюрам ВСФ.
Эпюрой называется график, характеризующий закон изменения какого-либо параметра (например, ВСФ, напряжения, перемещения, температуры и др.) по длине или высоте составной части конструкции. Эпюра позволяет установить местоположение опасного сечения, где вероятнее всего произойдет разрушение конструкции.
При построении эпюр необходимо придерживаться следующих общих правил и порядка.
Правила построения эпюр ВСФ:
- ось, или база, эпюры выбирается рядом с исходной расчетной схемой;
- ординаты эпюры откладываются от оси в некотором масштабе с учетом знака;
- поле эпюры подвергается штриховке (штриховые линии должны быть перпендикулярны к оси эпюры), внутри него указывается знак и обозначаются характерные ординаты эпюры;
- выше или рядом с эпюрой дается ее название и указывается размерность, если эпюра построена в числовом виде.
Порядок построения эпюр ВСФ:
|
|
|
- расчетная схема заданного бруса разбивается на силовые участки, то есть участки, в пределах которых закон изменения заданного фактора является одним и тем же, т.е. неизменным. Границами силовых участков являются сечения, в пределах которых действуют внешние нагрузки (M, F, q) или изменяются направление оси и поперечные размеры бруса;
- для каждого силового участка применяется метод сечений (правило “РОЗУ”) и составляется общее уравнение искомого ВСФ в виде функции переменной абсциссы z ;
l GWrxXVdgqZdd/oXiBz4jST5C5jRewUd4LmTutTRczGdPitvVKhFqlYhwUhxmlQgBgp+qj6D50m65 pQWVSywVvlrPbsMilH+nHYonkZmu0ngeZe/+DwAA//8DAFBLAwQUAAYACAAAACEAwEI0D+IAAAAK AQAADwAAAGRycy9kb3ducmV2LnhtbEyPwW7CMBBE75X6D9ZW6g1sQ9NCiIMQantClQqVKm4mXpKI eB3FJgl/X/fUHlfzNPM2W4+2YT12vnakQE4FMKTCmZpKBV+Ht8kCmA+ajG4coYIbeljn93eZTo0b 6BP7fShZLCGfagVVCG3KuS8qtNpPXYsUs7PrrA7x7EpuOj3EctvwmRDP3Oqa4kKlW9xWWFz2V6vg fdDDZi5f+93lvL0dD8nH906iUo8P42YFLOAY/mD41Y/qkEenk7uS8axRkMgIKphIIZbAIvC0eEmA nRTMxHwJPM/4/xfyHwAAAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAAAAAA AAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQBAAAL AAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQAHFfQ+egwAAEOqAAAO AAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQDAQjQP4gAAAAoB AAAPAAAAAAAAAAAAAAAAANQOAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAA4w8AAAAA " o:allowoverlap="f">
| F |
| l |
| M |
| Q |
| Рисунок 2.6- Пример построения эпюр ВСФ |
| F |
| F×l |
|
|
|
При построении эпюр ВСФ предварительно устанавливаются правила знаков, которые являются условными для каждого ВСФ
22) Состояние растяжение-сжатие. Определение напряжений в поперечном сечении (без учета и с учетом собственного веса).
Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы 
, а прочие силовые факторы равны нулю.
Рассмотрим однородный прямолинейный стержень длиной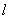 
и площадью поперечного сечения А, на двух концах которого приложены две равные по величине и противоположно направленные центральные продольные силы Р (рис. 2.2, а).
Продольная сила – внутреннее усилие, равное сумме проекций всех внешних сил, взятых с одной стороны от сечения, на ось стержня. Примем следующее правило знаков дляпродольной силы: растягивающая продольная сила положительна, сжимающая – отрицательна (рис. 2.1).
Рис.2.1
Поместим начало плоской системы координат yz в центре тяжести левого сечения, а ось 
направим вдоль продольной оси стержня.
Для определения величин внутренних усилий воспользуемся методом сечений. Задавая некоторое сечение на расстояние z ( 
) от начала системы координат и рассматривая равновесие левой относительно заданного сечения части стержня (рис. 2.2, б), приходим к следующему уравнению:
|
|
|
,
откуда следует, что
.
Следовательно, продольная сила в сечении численно равна сумме проекций на ось стержня всех сил, расположенных по одну сторону сечения
(2.1) 
Рис. 2.2
Для наглядного представления о характере распределения продольных сил по длине стержня строится эпюра продольных сил . Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.
Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти Nmax при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.
Отсутствует пример расчета. Его я не нашел к сожалению.
23) Определение деформации при растяжении-сжатии.
Oпыты показывают, что при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются, при сжатии - наоборот (рис.2.7).
Абсолютная продольная и поперечная деформации равны
|
|
|
; 
.
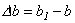Относительная продольная деформация e и относительная поперечная деформация e' равны
; 
.
В пределах малых удлинений для большинства материалов справедлив закон Гука - нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформацииe
. (2.2)
Коэффициент пропорциональности E - модуль продольной упругости, его величина постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки.
Средние значения E и m для некоторых материалов даны в таблице 1.1.
Таблица 1.1
Значения модуля упругостиЕ и коэффициента Пуассона n
| Материал | Е, МПа | n |
| Сталь | (2-2.2)×105 | 0.24-0.3 |
| Титан | 1.1×105 | 0.25 |
| Алюминий | 0.7×105 | 0.32-0.36 |
| Медь | 1.0×105 | 0.31-0.34 |
| Чугун | (1.1-1.6)×105 | 0.23-0.27 |
| Резина | 1.0-0.8 | 0.5 |
| Пробка | - | 0 |
| Стекловолокно | (0.18-0.4)×105 | 0.25 |
| Дерево | 1×104 | - |
Так как , а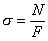 
, то подставляя в закон Гука (2.2) можно получить формулу для определения абсолютного удлинения (укорочения) стержня
.
Эта зависимость также выражает закон Гука.
Знаменатель EF называется жесткостью при растяжении - сжатии или продольной жесткостью.
Отношение относительной поперечной деформации e' к относительной продольной деформации e, взятое по модулю, называется коэффициентом поперечной деформации иликоэффициентом Пуассона
.
Эта величина является постоянной для каждого материала и определяется экспериментально.
Значения n для различных материалов изменяются в пределах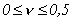 
(n= 0 у пробки, n= 0,5 у резины). Для большинства конструкционных материалов n=0,25…0,33 (табл. 1.1).
E и n являются основными характеристиками упругости изотропного материала.
24) Закон Гука при растяжении-сжатии и сдвиге.
Растяжение сжатие:
Закон Гука выражает прямо пропорциональную зависимость между нормальным напряжением и относительной деформацией: 
или, если представить в другом виде: 
где Е - модуль продольной упругости. Это физическая постоянная материапа, характеризующая его способность сопротивпяться упругому деформированию.
Закон Гука при сдвиге: g = t/G или t = G×g .
G — модуль сдвига или модуль упругости второго рода [МПа] — постоянная материала, характеризующая способность сопротивляться деформациям при сдвиге. (Е — модуль упругости, m— коэффициент Пуассона).
Потенциальная энергия при сдвиге: .
Удельная потенциальная энергия деформации при сдвиге: ,
где V=а×F — объем элемента. Учитывая закон Гука, .
Вся потенциальная энергия при чистом сдвиге расходуется только на изменение формы, изменение объема при деформации сдвига равно нулю.
Закон Пуассона.
вероятность возникновения случайного события n раз за время t. l - интенсивность случайного события.
Свойства:
1) МО числа событий за время t: М = l*t.
2) среднеквадратическое отклонение числа событий 
, для данного распределения М = D.
Распределение Пуассона получается из биноминального, если число испытаний m неограниченно возрастает, а МО числа событий остается постоянным.
Закон Пуассона используется в том случае когда необходимо определить вероятность того что за данное время произойдет 1,2,3…отказов.
Дата добавления: 2018-02-15; просмотров: 1010; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!