АЛГОРИТМЫ ПОЛУЧЕНИЯ СЛУЧАЙНЫХ ЧИСЕЛ С ЗАДАННЫМ РАСПРЕДЕЛЕНИЕМ

⇐ ПредыдущаяСтр 2 из 5Следующая ⇒

Случайные числа с заданным распределением программно имитируются на базе использования квазиравномерных случайных чисел R. Существует много вычислительных процедур, позволяющих имитировать как непрерывные так и дискретные вероятностные распределения, заданные плотностью распределения f(x) либо функцией распределения F(x).

Для имитации случайных величин широко применяется метод обратных функций. Пусть требуется имитировать значения случайной величины Х с функцией распределения F(x). Доказано, что, если значения квазиравномерных чисел R брать в качестве значений функции распределения , то соответствующие им значения x аргумента функции F(x) (значения обратной функции) образуют выборку чисел, распределенных в соответствии с законом F(x).

Обратная функция в ряде случаев может быть получена аналитически. В противном случае, а также для дискретных распределений используются соответствующие алгоритмы.

Схема генерации значений случайной величины для случая, когда указанное уравнение не удается решить, иллюстрируется на рисунке 1. На рисунке показана функция распределения дискретной случайной величины Х ( ). Действительно, значениям величины - можно поставить в соответствие вероятности , рассчитанные по значениям функции распределения как = - .

Указанные значения образуют полную группу событий 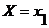, …, , а задача генерации сводится к задаче моделирования полной группы независимых элементарных событий и графически означает ”набрасывание” значений квазиравномерной случайной величины на отрезок единичной длины по оси 0-Y.

Для многих законов распределений существуют специальные алгоритмы генерации, основанные на свойствах и особенностях этих распределений. Качество таких алгоритмов, как правило, выше качества универсальных алгоритмов.

Равномерное распределение

Равномерное распределение непрерывной случайной величины X описывается функциями плотности и распределения, представленными в § 1 и ниже на рисунках 1, 2.

Параметрами распределения являются произвольные значения a и b (a < b) , которые задают интервал распределения.

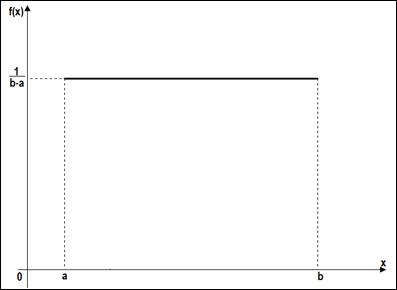
Рис. 2. Функция плотности равномерного распределения

Рис. 3. Функция распределения равномерного распределения

Используем метод обратных функций и аналитическое описание функции распределения

и запишем соответствующее уравнение

Решив уравнение, получим аналитическое выражение для имитации значений равномерно распределенных случайных величин в заданном диапазоне значений как .

Алгоритм имитации сводится к выполнению следующих операций:

1. Генерируется значение R_i квазиравномерной случайной величины (в диапазоне 0-1).

2. Вычисляется по формуле искомое значение x_i.

3. Возврат на пункт 1.

Пример использования алгоритма для имитации равномерно распределенных величин на интервале от a =-3 до b=7.

Пусть сгенерированы значения квазиравномерной величины R: 0.43, 0.80, 0.29, 0.67, 0.19.

Ниже для выбранных в примере исходных установок представлены результаты имитации первых значений последовательности:

Нормальное распределение

Нормальное (Гауссовское) распределение является одним из наиболее распространенных непрерывных распределений. Описывается функцией плотности, представленной ниже и изображенной на рисунке 4.

Параметрами распределения являются значения и 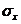- соответственно математическое ожидание и среднее квадратическое отклонение распределения. Стандартным нормальным распределением называется распределение с математическим ожиданием равным нулю и стандартным отклонением единица.

Изменение параметра нормального распределения приводит к сдвигу графика по оси x. Изменение параметра нормального распределения приводит к масштабированию формы графика по оси x.

Алгоритм для имитации нормального распределения может быть получен на основе центральной предельной теоремы, согласно которой сумма независимых случайных величин с произвольными распределениями имеет асимптотически гауссовское распределение.

При этом сходимость к нормальному распределению проявляется быстрее, если суммируются величины с одинаковым распределением.

Соответственно в основе имитационного алгоритма лежит суммирование значений случайной квазиравномерной величины R. Соответствующая формула приведена ниже

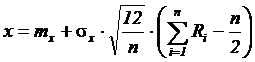В ряде практических приложений удовлетворительные результаты могут быть получены уже для значений n = 6, тогда соответствующая формула принимает вид

Рис. 4. Функции плотности нормального распределения

Пример использования алгоритма для имитации гауссовского распределения с параметрами и .

Пусть сгенерированы следующие значения квазиравномерной величины R: 0.43, 0.80, 0.29, 0.67, 0.19, 0.96, 0.02, 0.73, 0.50, 0.33 0.14, 0.71.

Дата добавления: 2018-02-15; просмотров: 1082; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 Следующая ⇒

Мы поможем в написании ваших работ!