Мультипликативный и смешанный (конгруэнтные) методы

Стр 1 из 5Следующая ⇒

Министерство образования Республики Беларусь

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«БРЕСТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Методические рекомендации

(методическое пособие )

“ИМИТАЦИЯ СЛУЧАЙНЫХ ОБЪЕКТОВ”

БРЕСТ 2011

УДК 681.3 (075.8)

ББК с57

Учреждение образования “Брестский государственный технический университет”

Кафедра интеллектуальных информационных технологий

Рекомендовано к изданию редакционно-издательским советом

Брестского государственного технического университета

Рецензент: заведующий кафедрой высшей математики Брестского государственного технического университета, к.т.н. Махнист Л.П.

Авторы-составители: Г.Л. Муравьев, доцент, к.т.н., Ю.В. Савицкий, доцент, к.т.н., С.В. Мухов, доцент, к.т.н.

ИМИТАЦИЯ СЛУЧАЙНЫХ ОБЪЕКТОВ. Г.Л. Муравьев, Ю.В. Савицкий, С.В. Мухов. – Брест.: БрГТУ, 2011. - 33 с.

Методическое пособие предназначено для знакомства с основами программной имитации случайных величин. Рассмотрены подходы и алгоритмы имитации базовых случайных величин, произвольных случайных величин с заданными вероятностными свойствами с использованием как универсальных так и специальных методов.

УДК 681.3 (075.8)

ББК с57

“Брестский государственный технический университет”, 2011

Введение

В имитационном моделировании систем, при моделировании систем методом Монте-Карло требуется воспроизводить, имитировать, генерировать значения случайных объектов с заданными вероятностными свойствами.

Это значения таких объектов как случайные события, системы событий, случайные величины и системы случайных величин, случайные последовательности и процессы.

Количество случайных чисел, требуемых для получения, прогнозирования статистически устойчивых оценок характеристик функционирования систем, изменяется в широких пределах в зависимости от особенностей моделируемой системы, вычисляемых характеристик и процедур их оценки, требуемой точности результатов моделирования.

При этом характеристики модели существенно зависят от качества используемых имитаторов случайных объектов. Соответственно быстродействие средств имитации случайных объектов в значительной степени определяет трудоемкость модели, а ее адекватность зависит, в том числе, от качества генерируемых последовательностей.

Наличие простых и экономичных способов формирования последовательностей случайных чисел требуемого качества во многом определяет возможность практического использования машинного моделирования систем.

АЛГОРИТМЫ ПОЛУЧЕНИЯ КВАЗИРАВНОМЕРНЫХ ЧИС ЕЛ

При программной реализации моделирования систем имитация случайных объектов любого типа сводится, как правило, к генерированию последовательностей значений некоторых стандартных, базовых случайных величин и к их последующему функциональному преобразованию.

Базовые случайные величины равномерно распределены на интервале (0; 1). Известно, что непрерывная случайная величина, распределенная равномерно в интервале (a; b), имеет аналитически описанные функцию плотности и функцию распределения:

Ее основные числовые характеристики приведены ниже:

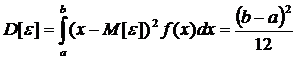
Соответственно функция плотности и функция распределения базовой случайной величины имеют вид:

А значения математического ожидания и дисперсии определяются формулами: и соответственно.

При имитационном моделировании и использовании вычислительных средств типовых компьютеров общего назначения, включая персональные компьютеры, приходится иметь дело с ограниченной разрядностью (n-разрядов) процессоров и эффектами замены непрерывных значений на дискретные, цифровые. Соответственно вместо значений непрерывной равномерно распределенной случайной величины в диапазоне (0; 1) приходится использовать выборку дискретной последовательности случайных чисел того же интервала, распределенных так же равномерно. Такие значения называют квазиравномерными.

Математическое ожидание и дисперсия квазиравномерной случайной величины имеют вид:

Видно, что если математическое ожидание квазиравномерной случайной величины совпадает с математическим ожиданием непрерывной равномерно распределенной случайной величины, то уже дисперсия принимает отличное значение.

Таким образом, производимые с помощью “идеального” генератора квазиравномерные числа должны иметь равномерное распределение, быть статистически независимыми и воспроизводимыми. Соответствующие последовательности должны иметь максимально возможный период повторяемости. Их генерация должна отличаться минимальным использованием вычислительных ресурсов компьютера.

Метод серединных квадратов

Указанный метод исторически является одной из первых процедур получения квазиравномерных чисел.

Алгоритм имитации последовательности квазиравномерных чисел приведен ниже:

1. Выбирается число разрядов - целое значение n.

2. Задается 2n-разрядное число x₀= a₁,a₂,…a_2n, меньшее единицы.

3. Текущее число x₀ возводится в квадрат (x₀)² = b₁,b₂…b_4n.

4. Определяется новое значение искомого числа x₁= b_n+1,b_n+2…b_3n, путем выделения 2n средних разрядов из квадрата исходного числа (x₀)².

5. В качестве x₀= x₁берется полученное число.

6. Возврат на пункт 3.

Пример использования алгоритма.

Пусть начальное число x₀= 0.2152, тогда (x₀)²= 0.04631104, соответственно первое полученное число x₁= 0.6311.

На следующем шаге значение x₀= 0.6311, тогда (x₀)²= 0.39828721, соответственно второе полученное число x₁= 0.8287.

Недостаток метода состоит в наличии корреляции между числами последовательности, причем в ряде случаев случайность вообще может отсутствовать. Кроме этого, при имитации последовательности может наблюдаться ее вырождение.

Например, если исходное число x₀= 0.0009, то (x₀)²= 0,00000081, а значение x₁= 0,0000 и т.д.

Указанное существенно ограничивает возможности использования метода серединных квадратов.

Мультипликативный и смешанный (конгруэнтные) методы

Наибольшее применение в практике имитационного моделирования на ЭВМ для программной генерации последовательностей псевдослучайных чисел нашли алгоритмы на базе рекуррентных соотношений, например, первого порядка

и их модификации. Здесь начальное значение числа x₀ и постоянные параметры функции Ф задаются пользователем.

Ниже рассматриваются некоторые процедуры получения последовательностей квазиравномерно распределённых чисел, которые нашли применение в практике имитационного моделирования систем при программной реализации генераторов.

Это, в частности, процедуры (метод вычетов) генерации на базе арифметических операций, в основе которых лежит понятие конгруэнтности.

Два целых числа α и β конгруэнтны (сравнимы) по модулю m, где m является целым числом, тогда, когда существует целое число k такое, что α – β = k · m. То есть указанная разность делится на m, числа имеют одинаковые остатки от деления на абсолютную величину числа m.

Например, конгруэнтны значения 1984 ≡ 4 (mod 10), 5008 ≡ 8 (mod 103) и т.д.

Сами конгруэнтные процедуры являются детерминированными, так как описываются рекуррентными соотношениями. Например, функция Ф может быть записана как

где значения x_i, множитель λ, аддитивная константа µ, модуль M представляют собой произвольные неотрицательные целые числа.

При этом, если задано начальное значение параметров x, λ и µ, то рекуррентное выражение определяет детерминированную (повторяющуюся) последовательность целых чисел { x_i}, где для любого i≥1 справедливо неравенство x_i< M.

На основе полученной ранее последовательности целых случайных чисел { xi } далее можно вычислить последовательность значений квазиравномерной случайной величины { x_i^0..1} = { x_i / M }, представляющих собой вещественные (рациональные) числа из интервала ( 0; 1).

В настоящее время практически все библиотечные функции языков высокого уровня, применяемые для вычисления последовательностей квазиравномерных случайных чисел, основаны на конгруэнтных процедурах.

Вычислительный алгоритм Лемера.Указанный алгоритм основан на применении рекуррентного соотношения

, где a и M положительные целые числа ( M > a ), и является вычислительной основой как смешанного так и мультипликативного методов, применяемых при программной реализации на ЭВМ.

Таким образом, вначале задаются значения a и M, а также исходное числоx₀. Далее согласно указанному соотношению результатпроизведения a·x_i берется по модулю M - определяется остаток от деления a·x_i на M. Полученное значение, находящееся в диапазоне 0 ≤ x_i+1< M, принимается в качестве значения “промежуточного” числа x_i+1.

На основе полученных целых чисел последовательности { xi } далее вычисляется последовательность значений квазиравномерной величины { x_i^0..1} = { x_i / M } в интервале ( 0; 1).

Качество генерируемых квазиравномерных чисел { x_i^0..1} определяется удачным выбором значений ”настроечных” параметров a, M, x₀. Здесь параметры a и x₀ влияют на статистические свойства получаемых чисел, а параметр M на период их повторения. Следовательно, выбор параметров a, M, x₀ должен осуществляться таким образом, чтобы обеспечить требуемые статистические свойства последовательности и наибольший период повторения.

Исходное значение x₀ должно быть достаточно большим, но меньше, чем 2^M–1. Рекомендуется в его качестве использовать простое число с большим количеством единичных бит в двоичном представлении.

Алгоритм имитации квазиравномерных чисел сводится к выполнению следующих операций:

1. Выбирается в качестве начального значения x₀ произвольное положительное целое число.

2. Выбираются целые положительные числа в качестве значений параметров a и M (M > a).

3. Находится произведение a ∙ x₀.

4. Вычисляется остаток от деления произведения a∙x₀ на M и принимается в качестве нового значения x₁.

5. Полученное значение преобразуется в вещественное значение из интервала (0; 1), то есть вычисляется квазиравномерное значение x₁^0..1 = x₁/ M.

7. Возврат на пункт 3.

Пример использования алгоритма.

Для случая g = 4 для нахождения каждого числа ( x₁^0..1 ) выполняются следующие действия:

1. Выбирается в качестве x₀ произвольное нечетное положительное целое число, например 7.

2. Выбираются a = 3 и M = 5 как целые положительные числа, где M > a.

3. Рассчитывается значение a ∙ x₀= 21.

4. В качестве искомого значения x₁ берется остаток от деления a∙x₀ на M, то есть x₁= 21 mod 5 = 1.

5. Определяется значение квазиравномерной величины из интервала (0; 1) как результат x₁^0..1= x₁/ M = 1/ 5 = 0,2.

6. Новое значение x₀устанавливается как x₀= 3.

7. Возврат на пункт 3.

Указанным образом может быть получено необходимое количество значений квазиравномерной величины. Ниже для выбранных в примере исходных установок представлены результаты имитации первых значений последовательности:

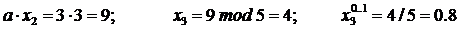
Указанная процедура получения квазиравномерных чисел может быть реализована мультипликативным либо смешанным методом. Ниже показаны особенности соответствующих алгоритмов с учетом ограниченной разрядности цифровых компьютеров и учетом используемой в них системы счисления.

Мультипликативный метод представляет собой частный случай использования приведенной конгруэнтной процедуры при µ = 0. Соответственно формула принимает вид

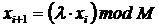
Для машинной реализации наиболее удобен случай, когда M = p^g, где переменная p - число цифр в системе счисления, принятой в ЭВМ, а переменная g - число символов (битов для двоичных слов) в машинном слове.

Тогда процедура вычисления остатка от деления на M сводится к выделению g младших разрядов делимого, а преобразование целого числа x_i в рациональную дробь из интервала x (0; 1) осуществляется простой “подстановкой” слева от полученного целого значения x_i запятой.

Алгоритм имитации квазиравномерных чисел (для случая использования двоичной системы счисления с ) сводится к выполнению следующих операций:

1. Выбирается в качестве начального значения x₀ произвольное нечетное число.

2. Вычисляется коэффициент λ, например, по правилу λ = 8^t∙ t ± 3, где t - любое целое положительное число.

3. Находится произведение λ ∙ x₀, содержащее не более 2^g значащих разрядов.

4. Берется g младших разрядов произведения в качестве искомого значения x₁, остальные разряды отбрасываются.

5. Полученное значение приводится к вещественному из интервала (0; 1), то есть вычисляется квазиравномерное значение x₁^0..1 = x₁/ 2^g .

6. В качестве нового значения x₀берется полученное число x₀= x₁.

7. Возврат на пункт 3.

Пример использования алгоритма.

Для случая g = 4 (это значение g выбрано в целях упрощения расчетов в демонстрационном примере) для нахождения каждого числа ( x₁^0..1 ) выполняются следующие действия:

1. Выбирается в качестве x₀ произвольное нечетное число, например 7.

2. Выбирается t = 1 и вычисляется коэффициент λ. Из двух вариантов λ = 5 и λ = 11 выберем λ = 5.

3. Рассчитывается λ ∙ x₀= 35, что в двоичной системе счисления составляет 35₁₀= 00100011₂. Полученное число содержит 6 ≤ 8 значащих разрядов.

4. В качестве искомого значения x₁ берется 4 младших разряда x₁= 0011 = 3₁₀, а остальные разряды отбрасываются.

5. Определяется значение квазиравномерной величины из интервала (0; 1) как результат x₁^0..1= 3 / 2⁴= 0,1875.

6. Новое значение устанавливается как x₀= 3.

7. Возврат на пункт 3.

Указанным образом может быть получено необходимое количество значений квазиравномерной случайной величины. Ниже для выбранных в примере исходных установок представлены результаты имитации первых значений последовательности:

Смешанный метод базируется на использовании исходной формулы

С вычислительной точки зрения смешанный метод сложнее мультипликативного на операцию сложения, но при этом возможность выбора дополнительного параметра позволяет повысить качество имитации, уменьшить возможную корреляцию получаемых чисел.

1. Выбирается в качестве начального значения x₀ произвольное нечетное число.

2. Выбирается в качестве µ произвольное неотрицательное целое число (0 < μ < M).

3. Вычисляется коэффициент λ = λ = 8^t∙ t ± 3, где t - любое целое положительное число.

4. Находится значение λ ∙ x₀+ μ, содержащее не более 2g значащих разрядов.

5. Берется g младших разрядов значения λ∙x₀+μ в качестве искомого значения x₁, остальные разряды отбрасываются.

6. Полученное значение приводится к вещественному из интервала (0; 1), то есть вычисляется квазиравномерное значение x₁^0..1 = x₁/ 2^g .

7. В качестве x₀= x₁берется полученное число.

8. Возврат на пункт 3.

Пример использования алгоритма.

1. Выбирается в качестве x₀ произвольное нечетное число 7.

2. Выбирается в качестве µ произвольное неотрицательное целое число 3.

3. Выбирается t = 1 и вычисляется коэффициент λ. Из двух вариантов λ = 5 и λ = 11 выберем λ = 5.

4. Рассчитывается λ ∙ x₀+ μ = 38, что в двоичной системе счисления составляет 38₁₀= 00100110₂. Полученное число содержит 6 ≤ 8 значащих разрядов.

5. В качестве искомого значения x₁ берется 4 младших разряда x₁= 0110₂= 6₁₀, а остальные разряды отбрасываются.

6. Определяется значение квазиравномерной величины из интервала (0; 1) как результат x₁^0..1= 6 / 2⁴= 0,75.

7. Новое значение устанавливается как x₀= 6.

8. Возврат на пункт 3.

Рекурсивный метод

Рекурсивный метод получения квазиравномерных чисел основан на применении следующих формул

, где a₀, a₁ – целые положительные коэффициенты;

M – целое положительное число, модуль;

Z_i– рассчитываемые целые положительные числа;

x_i – рассчитываемые квазиравномерные числа.

Таким образом, в качестве исходных параметров задаются значения a₀, a₁, M, Z_-1 и Z₀.

Алгоритм имитации квазиравномерных чисел сводится к выполнению следующих операций:

1. Выбираются произвольные целые положительные числа в качестве начального значения Z_-1 и Z₀.

2. Выбираются целые положительные числа в качестве значений a₀, a₁, M.

3. Вычисляется значение Z₁= a₀∙ Z_-1 + a₁∙ Z₀.

4. Вычисляется остаток от деления Z₁ на M и принимается в качестве искомого промежуточного значения x₁.

5. Полученное значение приводится к вещественному из интервала (0; 1), то есть вычисляется квазиравномерное значение x₁^0..1 = x₁/ M.

6. Возврат на пункт 3.

Пример использования алгоритма.

1. Выбираются в качестве Z_-1 и Z₀ произвольные целые положительные числа, например, 12345 и 97531 соответственно.

2. Выбираются целые положительные числа в качестве значений a₀= 1, a₁ = 1, M = 5000.

3. Рассчитывается значение Z₁= 109876.

4. В качестве искомого значения x₁ берется x₁= 109876 mod 5000 = 4876.

5. Определяется значение квазиравномерной величины из интервала (0; 1) как результат x₁^0..1= 4876 / 5000 = 0,9752.

6. Возврат на пункт 3.

Метод Таусворта

Метод получения квазиравномерных случайных чисел Таусворта основан на применении следующих формул

Здесь используются следующие переменные:

- r, q целые положительные числа;

- B₀ бинарный (двоичный) вектор длины 2q;

- b_i компоненты бинарного вектора B₀;

- x_i+1 генерируемое квазиравномерное число с двоичным представлением b_q₊₁ b_q₊₂… b₂_q.

В качестве параметров задаются значения r и q, а также первые q компонентов бинарного вектора B₀, то есть значения q начальных бит с номерами 1- q.

Алгоритм имитации квазиравномерных чисел сводится к выполнению следующих операций:

1. Выбираются в качестве r и q произвольные целые положительные числа, вычисляется значение M = 2^q.

2. Задаются первые q компонент бинарного вектора B₀.

3. Вычисляются вторые q компонент бинарного вектора B₀, то есть значения битов b_q₊₁ b_q₊₂… b₂_q по формуле b_j = (b_j_-_r + b_j_-_q ) mod 2, где q + 1 j 2q.

4. Выполняется перевод полученного бинарного вектора из двоичного представления в десятичное. Полученное значение принимается в качестве искомого значения x₁.

5. Полученное значение приводится к вещественному из интервала (0; 1), то есть вычисляется квазиравномерное значение x₁^0..1 как x₁/ M.

6. Модифицируются первые q компонент бинарного вектора B₀ путем соответствующего переприсваивания значений битов b_j = b_q+jдля 1 j q.

7. Возврат на пункт 3.

Пример использования алгоритма.

1. Выбираются в качестве r = 3 и q = 8 произвольные целые положительные числа, вычисляется M = 2⁸= 256.

2. Задаются первые q компонентов бинарного вектора B₀ b₁b₂b₃b₄b₅b₆b₇b₈ = 11010010.

3. Вычисляются вторые q компонентов вектора B₀ как

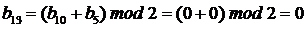Соответственно значение .

4. Вычисляется x₁= 10000010₂= 130₁₀;

5. Полученное значение приводится к вещественному из интервала (0; 1), то есть вычисляется квазиравномерное значение .

6. Модифицируются первые q компонент бинарного вектора B₀ путем соответствующего переприсваивания значений бит.

7. Возврат на пункт 3.

Сложный метод

Сложный метод основан на применении следующих формул

;

Здесь используются следующие переменные:

- a₀, a₁, b₀, b₁, c₀, c₁ целые положительные коэффициенты;

- Z_t1, Z_t2 , Z⁰₁, Z¹₁, Z⁰₂, Z¹₂ вспомогательные целые числа;

- x_i рассчитываемые квазиравномерные числа.

В качестве параметров задаются значения a₀, a₁, b₀, b₁, c₀, c_1,Z⁰₁, Z⁰₂.

Алгоритм имитации квазиравномерных чисел сводится к выполнению следующих операций:

1. Выбираются произвольные целые положительные числа в качестве значения a₀, a₁, b₀, b₁, c₀, c₁ .

2. Выбираются произвольные целые положительные числа в качестве начального значения Z⁰₁, Z⁰₂, вычисляются значения Z¹₁= Z⁰₁ и Z¹₂= Z⁰₂.

3. Вычисляются значения Z_t1, Z_t2 по формулам:

4. Вычисляется искомое промежуточное значение x₁ по формуле

x_i = (|Z_t₁ – Z_t₂|) mod c₀.

5. Полученное значение приводится к вещественному из интервала (0; 1), то есть вычисляется квазиравномерное значение x₁^0..1 = x₁/ c₀ .

6. Модифицируются значения Z⁰₁ = Z¹₁, Z¹₁ = Z_t1, Z⁰₂ = Z¹₂, Z¹₂ = Z_t2.

7. Возврат на пункт 3.

Пример использования алгоритма.

1. Выбираются значения параметров a₀= 14, a₁= 5, b₀= 81, b₁= 139, c₀= 4294, c₁= 9494.

2. Задаются Z⁰₁, Z⁰₂, вычисляются Z¹₁= Z⁰₁ и Z¹₂= Z⁰₂ как Z⁰₁ = Z¹₁= 13511, Z⁰₂ = Z¹₂= 1477.

3. Вычисляются значения Z_t1, Z_t2 как

Z_t1= ( | 14∙13511 - 81∙13511 | ) mod 4294 = 3497,

Z_t2= ( | 5∙1477 - 139∙1477 | ) mod 9494 = 8038.

4. Вычисляется значение x₁ по формуле ( | 3497 – 8038 | ) mod 4294 = 247.

5. Определяется x₁^0..1 = 247 / 4294 = 0,05752212.

6. Модифицируются значения Z⁰₁ = 13511, Z¹₁ = 3497, Z⁰₂ = 1477, Z¹₂ = 8038.

7. Возврат на пункт 3.

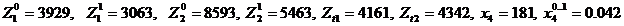
Дата добавления: 2018-02-15; просмотров: 1894; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 Следующая ⇒

Мы поможем в написании ваших работ!