Экспоненциальное распределение

Экспоненциальное распределение непрерывной случайной величины X описывается функциями плотности и распределения, представленными ниже и изображенными на рисунках 5, 6

 

       ,          

  .                 

 

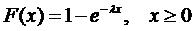Параметром распределения является значение λ – интенсивность (или обратный коэффициент масштаба), λ > 0. Соответственно математическое ожидание и дисперсия случайной величины X определяется соотношениями

 ,   .

Используем метод обратных функций и аналитическое описание функции распределения экспоненциального закона 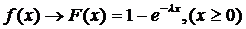. Соответственно получим уравнение  .

 

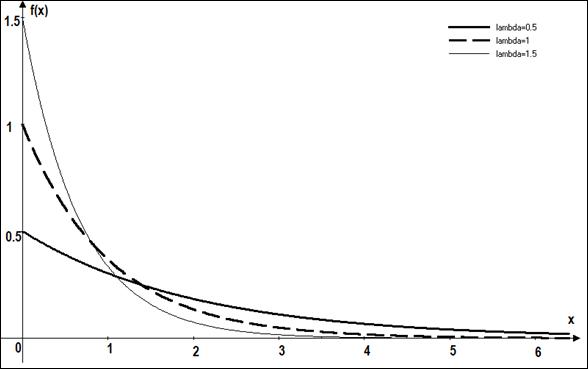
Рис. 5. Функция плотности экспоненциального распределения

 

Решив уравнение, получим аналитическое выражение для имитации значений равномерно распределенных случайных величин

 или    .      

Рис. 6. Функция распределения экспоненциального распределения

 

Пример использования алгоритма для имитации экспоненциального распределения с параметром λ = 0,8.

Пусть сгенерированы значения квазиравномерной величины R: 0.43, 0.80, 0.29, 0.67, 0.19.

Ниже для выбранных в примере исходных установок представлены результаты имитации первых значений последовательности:

 

Гамма-распределение

Гамма-распределение представляет собой двухпараметрическое семейство непрерывных распределений (положительных значений случайной величины). Описывается функцией плотности, представленной ниже и изображенной на рисунке 7

 

                     

 

Гамма-распределение задается двумя параметрами: параметром формы η и λ, где оба параметра вещественные положительные числа (η > 0 и λ > 0).

Если η принимает только целочисленные значения, то гамма-распределение сводится к распределению Эрланга η-го порядка.

Соответственно при η = 1 гамма-распределение сводится к экспоненциальному распределению.

Указанные параметры определяют характеристики случайной величины. Соответственно математическое ожидание и дисперсия определяется как

 ,   .

 

 

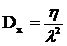Рис. 7. Функция плотности гамма-распределения

 

Вид функции распределения для некоторых значений параметра η представлен ниже:

 

 

 

.

 

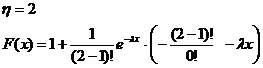
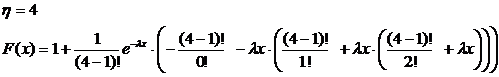Алгоритм имитации основан на следующем свойстве распределения. Сумма независимых экспоненциально распределенных случайных величин 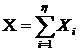имеет асимптотически гамма-распределение. Соответственно имитационный  алгоритм базируется на формуле

.                      

 

Пример использования алгоритма для имитации гамма-распределение с параметрами η = 3 и λ = 0,8.

Пусть сгенерированы значения квазиравномерной величины R: 0.43, 0.80, 0.29, 0.67, 0.19, 0.96, 0.02, 0.73, 0.50, 0.33 0.14, 0.71.

Ниже для выбранных в примере исходных установок представлены результаты имитации первых значений распределения:

 

.

 

Треугольное распределение

Произвольное треугольное распределение имеет функцию плотности соответствующего ”треугольного” вида и задается следующими параметрами: произвольными значениями a и b ( a < b ) , которые задают интервал распределения и параметром с – модой распределения.

В частном случае используется левостороннее, правостороннее, симметричное треугольное распределение случайной величины.

Математическое ожидание треугольного распределения составляет ( a + b + c ) / 3, а дисперсия ( a² + b² + c² – ab – ac – bc ) / 18.

Распределение Cимпсона.Распределение Симпсона или треугольное распределение описывается функцией плотности распределения, представленной ниже и изображенной на рисунке 8

                                 

 

Параметрами распределения являются произвольные значения a и b (a < b) , которые определяют интервал распределения и положение моды как a +  b.

 

Рис. 8. Функция плотности распределения Симпсона

 

Математическое ожидание и дисперсия могут быть рассчитаны по вышеприведенным формулам. Например, значение математического ожидания здесь составляет ( a + b ).

 

Алгоритм имитации базируется на следующем свойстве распределения.

Сумма , где y и z независимые случайные величины, распределенные равномерно на интервале , имеет распределение Симпсона. То есть распределение Симпсона можно рассматривать как композицию двух одинаковых законов равномерного распределения.

Соответственно алгоритм имитации сводится к выполнению следующих операций:

1. Генерируется пара значений квазиравномерной случайной величины.

2. Генерируется пара значений, распределенный равномерно на интервале .

3. Вычисляется искомое значение как сумма двух равномерно-распределенных значений .

4. Возврат на пункт 1.

 

Пример использования алгоритма для имитации распределения Симпсона с параметрами a = 6 и b = 7.

Пусть сгенерированы значения квазиравномерной величины R: 0.6445, 0.0898, 0.9883, 0.8711, 0.5820, 0.4023, 0.4258, 0.6836.

Ниже для выбранных в примере исходных установок представлены результаты имитации первых значений последовательности:

 

 

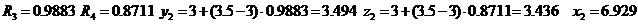
“Левостороннее” треугольное распределение. В частном случае (когда мода совпадает с одной из границ интервала) треугольное распределение может представлять собой линейно нарастающее (левостороннее распределение) либо убывающее (правостороннее распределение) распределение случайной величины X и описывается функциями плотности, представленными ниже и изображенными на рисунке 9 (для левостороннего распределения)

 

                         

 

и

 

              .

 

Параметрами распределения являются произвольные значения a и b (a < b) , которые задают интервал распределения.

 

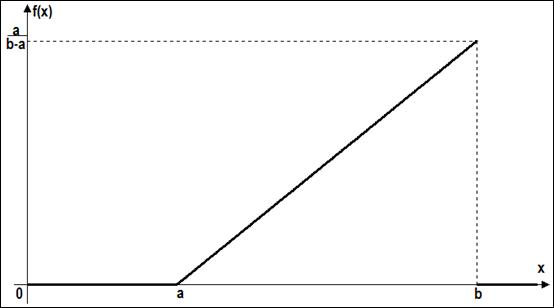
Рис. 9. Функция плотности треугольного распределения

 

Математическое ожидание и дисперсия могут быть рассчитаны по вышеприведенным формулам. Соответственно  здесь их значения определяются выражениями  

 и   .

Алгоритм имитации может быть построен на методе исключения И. Неймана.

Тогда для  имитации треугольного распределения следует:

1. Генерировать пару квазиравномерных случайных чисел R₁ и R₂.

2. Проверить условие R₂ < R₁. Если условие выполняется, то искомое значение находится по формуле . В противном случае пара R₁ , R₂ отбрасывается.

3. Повторяется  шаг 1.

 

Для  имитации треугольного распределения с функцией плотности, заданной второй формулой, следует:

1. Генерировать пару квазиравномерных  случайных чисел R₁ и R₂.

2. Проверить условие R₁ < R₂. Если условие выполняется, то искомое значение находится по формуле . В противном случае пара R₁ , R₂ отбрасывается.

3. Повторяется  шаг 1.

 

Альтернативный алгоритм имитации основан на использовании формул:

 

,                                 

.                                 

 

Пример использования алгоритма для имитации “левостороннего” треугольного распределения с параметрами a = -3 и b = 7.

Пусть сгенерированы значения квазиравномерной величины R: 0.43, 0.80, 0.29, 0.67, 0.19, 0.96, 0.02, 0.73, 0.50, 0.33 0.14, 0.71.

Ниже для выбранных в примере исходных установок представлены результаты имитации начальных значений:

 

.

 

---

Дата добавления: 2018-02-15; просмотров: 1490; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!