Распределение Эрланга k-го порядка

⇐ ПредыдущаяСтр 4 из 5Следующая ⇒

Распределением Эрланга k-го порядка называется распределение, описывающее непрерывную случайную величину X, принимающую положительные значения в интервале (0; + ∞) и представляющую собой сумму k независимых случайных величин, распределенных по одному и тому же экспоненциальному закону с параметром λ.

При k = 1 распределение Эрланга вырождается в экспоненциальное, а при k -> ∞ – приближается к нормальному распределению.

Распределение Эрланга представляет собой частный случай гамма-распределения при целочисленном значении параметра формы k (см. § 2.4). Функция плотности распределения представлена ниже

Здесь параметры: k ≥ 1 – целое число, λ > 0 - интенсивность (или обратный коэффициент масштаба). Математическое ожидание и дисперсия .

Алгоритм имитации основан на использовании формулы

Пример использования алгоритма для имитации распределения Эрланга с параметрами к = 3 и λ =1,3.

Пусть сгенерированы значения квазиравномерной случайной величины R на интервале: 0.43, 0.80, 0.29, 0.67, 0.19, 0.96, 0.02, 0.73, 0.50, 0.33 0.14, 0.71.

Ниже для выбранных в примере исходных установок представлены результаты имитации первых значений последовательности:

Гиперэкспоненциальное распределение

Гиперэкспоненциальное распределение непрерывной случайной величины, принимающей неотрицательные значения, представляет собой аддитивную композицию разных экспоненциальных распределений. Характерной особенностью распределения является то, что коэффициент вариации принимает значения большие единицы.

Описывается функцией плотности, представленной ниже

Соответственно гиперэкспоненциальное распределение задается параметрами:

Здесь n - количество “смешиваемых” экспоненциально распределённых случайных величин с отличающимися параметрами , а вектор задает вес каждой случайной величины в виде вероятности использования ее значения.

Математическое ожидание и дисперсия распределения определяются соответственно выражениями

и .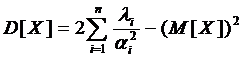

Алгоритм имитации случайных величин с гиперэкспоненциальным распределением.

Пусть имеется n генераторов экспоненциально распределённых случайных величин с отличающимися параметрами , и пусть вероятность взятия числа с i-го генератора задается распределением вероятностей .

Тогда в результате одного опыта с вероятностью α_i вырабатывается только одна случайная величина, а именно - полученная i-м генератором. Совокупность таких случайных величин, полученных в результате проведения множества опытов, и будет подчиняться гиперэкспоненциальному закону:

Соответственно:

- по равномерному закону “разыгрывается” номер генератора (см. § 2.1);

- генерируется экспоненциально-распределенное значение с использованием параметра выбранного генератора (см. § 2.3);

- полученное число является искомым, а процесс повторяется сначала.

ОЦЕНКА РЕЗУЛЬТАТОВ

Результаты имитационного моделирования, как правило, представляют собой наборы случайных чисел - реализаций случайных процессов, описывающих качество функционирования моделируемого объекта.

К типовому набору обычно оцениваемых характеристик относят статистические оценки точечных характеристик, моментов случайных величин.

В качестве статистической оценки измеряемой величины используют результаты вычислительных процедур, формул, обладающих свойствами несмещённости, состоятельности и эффективности.

Несмещённость означает, что оценка не содержит методическую ошибку. Состоятельность означает, что точность оценки растет с увеличением числа опытов, а эффективность, что оценка обладает лучшей “сходимостью” - минимальным разбросом значений по сравнению с другими оценками той же величины.

Оценка математическиго ожидания. Математическое ожидание относится к числу наиболее важных и часто используемых точечных характеристик случайных величин. Если в результате наблюдений, проведения экспериментов, в ходе имитационного моделирования получена совокупность N численных значений случайной величины Х - x₁, x₂, …, x_N, то в качестве оценки математического ожидания используется среднее арифметическое наблюдаемых значений (выборочное среднее)

Эта оценка является несмещенной, так как ее математическое ожидание в точности совпадает с реальным значением m

Оценка дисперсии. Другой важной точечной характеристикой случайных величин является дисперсия, позволяющая оценивать степень рассеивания возможных значений случайной величины относительно ее математического ожидания (средне взвешенного значения). В качестве оценки дисперсии принимается значение, определяемое формулой

Рекуррентное вычисление оценок. В ряде случаев необходимо вычислять текущие значения оценок, например, прямо в ходе проведения моделирования, и уточнять их по мере появления новых значений. Для “скользящей” оценки математического ожидания и дисперсии используют следующие рекуррентные формулы

, .

Здесь значение представляет собой оценку математического ожидания, полученную по выборке из N первых значений случайной величины.

Доверительные интервалы. При работе со статистическими оценками необходимо располагать данными о их надежности, точности. Такие данные в виду случайного поведения самих оценок могут иметь только предсказательный, вероятностный характер. В математической статистике в их качестве применяют доверительные интервалы I = ( a^*-ε, a^*+ε ) и соответствующие доверительные вероятности β.

Здесь a* - статистическая оценка искомой характеристики а, величина ε - погрешность вычисления характеристики, а вероятность β характеризует степень доверия к оценке и ее погрешности. Соответственно указанные величины связаны соотношением

Указанное означает, что реальное значение a оцениваемой характеристики окажется в пределах доверительного интервала I = ( a^*- ε, a^*+ ε ) с вероятностью β. Здесь значение вероятности α = 1 - β называется уровнем значимости.

Для полученной в результате наблюдений оценки среднего m* доверительный интервал вычисляется как , где значение погрешности в зависимости от требуемого уровня доверия - выбранного значения вероятности β рассчитывается как значение ε = σ^*_m_*∙ t .

Аналогичным образом рассчитывается доверительный интервал для оценки дисперсии, где значение ε = σ^*_D_*∙t .

Параметр t для выбранной доверительной вероятности β рассчитывается по формуле через функцию Лапласа F. Табличные значения параметра приведены в таблице 1.

Таблица 1. Значения параметра t(β)

β	t	β	t	β	t	β	t
0.8	1.282	0.86	1.475	0.92	1.750	0.98	2.325
0.81	1.310	0.87	1.513	0.93	1.810	0.99	2.576
0.82	1.340	0.88	1.539	0.94	1.880	0.998	3.000
0.83	1.371	0.89	1.592	0.95	1.960	0.999	3.290
0.84	1.404	0.90	1.643	0.96	2.053
0.85	1.439	0.91	1.694	0.97	2.169

Пример.

Пусть требуется обработать выборку из 30 значений случайной величины Х: 10.5, 10.8, 11.2, 10.9, 10.6, 11.0, 10.8, 11.0, 11.6, 10.9, 10.5, 11.8, 10.2, 9.2, 10.2, 11.2, 10.3, 11.1, 11.8, 10.3, 10.7, 10.8, 11.2, 10.9, 10.1, 11.7, 10.8, 11.3, 11.0, 11.9.

Значения оценок математического ожидания, дисперсии, квадратического отклонения

, , .

Зададимся доверительной вероятностью β = 0,8 и по таблице определим значение параметра t как 1,282.

Вычислим доверительный интервал оценки математического ожидания. Значение . Тогда границы доверительного интервала составят и . А сам доверительный интервал .

Рассчитаем доверительный интервал оценки дисперсии. Для этого вычислим оценку центрального момента четвертого порядка и среднеквадратическое отклонение D* как

и .

Значение . Тогда границы доверительного интервала составят и . А сам доверительный интервал .

В качестве приближенного значения оценки можно использовать .

ЛИТЕРАТУРА

1. Советов Б.Я., Яковлев С.А. Моделирование систем. Изд. 4-е. – М.: Высш. школа, 2005. – 343 с.

2. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для вузов. Изд. 7-е, стер. – М.: Высш. шк., 2000. – 479 с.

3. Колемаев В.А., Староверов О.В., Турундалевский В.Б. Теория вероятностей и математическая статистика: Учебное пособие для экономических специальностей вузов. – М.: Высш. шк., 1991. – 400 с.

Дата добавления: 2018-02-15; просмотров: 1397; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 Следующая ⇒

Мы поможем в написании ваших работ!