Понятие информации; понятие энтропии, избыточности; оценка энтропии дискретного и непрерывного источника; энтропия шумового сигнала

Федеральное агентство по образованию Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

«Южно-Уральский государственный университет»

Факультет «Приборостроительный»

Кафедра «Автоматика и управление»

 

 

РЕФЕРАТ

по курсу

"Общая теория связи"

 

 

                                                                           

 

 

                                                                           

                                                                       Выполнил:

                                                                       студент группы ПС–317

                                                                       ______________С.С. Плотников

                                                                       «____»________________2018 г.

 

                                                                           

                                                                       Проверила:

                                                                       ______________Т.А. Барбасова

                                                                       «____»________________2018 г.

 

Челябинск 2018

Оглавление

1 Распределение энергии в спектре периодического и непериодического сигнала; равенство Парсеваля; понятие о практической ширине частотного спектра сигнала.............................................................................................................................3
2 Принимаемый сигнал – как случайный процесс; виды случайных процессов, законы и числовые характеристики; корреляционные характеристики и свойства процессов; преобразования Винера-Хинчина; белый шум.......................................7
3 Векторное представление сигнала; дискретизация сигнала по времени; теорема отсчетов (Котельникова); дискретизация по уровню, шум квантования; условие ретрансляции; понятие ИКМ и ДМ сигнала...............................................................14
4 Понятие информации; понятие энтропии, избыточности; оценка энтропии дискретного и непрерывного источника; энтропия шумового сигнала...................18
5 Информационная характеристика сигнала: скорость передачи сигнала; бод, скорость передачи сигнала; пропускная способность дискретного сигнала в канале с помехами; пропускная способность канала с шумовой помехой; теорема Шеннона; согласование канала с сигналом................................................................21
6 Прямое и косвенное описание процессов; некоторые модели источников сообщений; модели речевого сообщения; модели стохастического дискретного источника..........................................................................................................................26
7 Идеальный канал без помех, канал с неопределенной фазой сигнала и аддитивным шумом, канал с межсимвольной интерференцией (МСИ) и аддитивным шумом.............................................................................................................................30
8 Модели дискретного канала, модели дискретного канала с память, модель дискретно-непрерывного канала..................................................................................31
Библиографический список......................................................................................37

 

Распределение энергии в спектре периодического и непериодического сигнала; равенство Парсеваля; понятие о практической ширине частотного спектра сигнала

 

Сигнал – это информационная функция, несущая сообщение о физических свойствах, состоянии или поведении какой-либо физической системы, объекта или среды, а целью обработки сигналов можно считать извлечение определенных информационных сведений, которые отображены в этих сигналах (кратко – полезная или целевая информация) и преобразование этих сведений в форму, удобную для восприятия и дальнейшего использования.

Формы представления сигналов.Кроме привычного динамического представления сигналов и функций в виде зависимости их значений от определенных аргументов (времени, линейной или пространственной координаты и т.п.) при анализе и обработке данных широко используется математическое описание сигналов по аргументам, обратным аргументам динамического представления. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой сколь угодно сложный по своей форме сигнал, не имеющий разрывов второго рода (бесконечных значений на интервале своего задания), можно представить в виде суммы более простых сигналов, и, в частности, в виде суммы простейших гармонических колебаний, что выполняется при помощи преобразования Фурье. Соответственно, математически разложение сигнала на гармонические составляющие описывается функциями значений амплитуд и начальных фаз колебаний по непрерывному или дискретному аргументу – частоте изменения функций на определенных интервалах аргументов их динамического представления. Совокупность амплитуд гармонических колебаний разложения называют амплитудным спектром сигнала, а совокупность начальных фаз – фазовым спектром. Оба спектра вместе образуют полный частотный спектр сигнала, который по точности математического представления тождественен динамической форме описания сигнала.

Спектральная форма представления сигнала – это представление параметров сигнала в виде двух графиков:

ü спектр амплитуд;

ü спектр фаз.

Спектральная диаграмма амплитуд показывает распределение энергии сигнала между составляющими его спектра. Структура спектра периодического сигнала полностью определяется значениями амплитуд и фаз гармоник. Высота линий спектра амплитуд пропорциональна амплитуде данной гармоники, поэтому их высоты различны. Основание спектральной линии на оси частот лежит в точке, соответствующей частоте гармоники. Длины линий спектра фаз пропорциональны значению фаз. Основание спектральной линии на оси частот лежит в точке, соответствующей частоте гармоники.

К периодическим относят гармонические и полигармонические сигналы. Для периодических сигналов выполняется общее условие s(t) = s(t + kT), где k = 1, 2, 3, ... – любое целое число, Т – период, являющийся конечным отрезком независимой переменной.

Гармонические сигналы(или синусоидальные), описываются следующими формулами:

s(t) = A×sin (2πf_оt+f) = A×sin (ω_оt+f),

s(t) = A×cos(ω_оt+φ),

где А, f_o, ω_o, φ, f – постоянные величины, которые могут исполнять роль информационных параметров сигнала: А – амплитуда сигнала, f_о – циклическая частота в герцах, ω_о = 2πf_о – угловая частота в радианах, φ и f – начальные фазовые углы в радианах. Период одного колебания T = 1/f_о = 2π/ω_o. При j = f – p/2 синусные и косинусные функции описывают один и тот же сигнал. Частотный спектр сигнала представлен амплитудным и начальным фазовым значением частоты f_о (при t = 0).

Полигармонические сигналы составляют наиболее широко распространенную группу периодических сигналов и описываются суммой гармонических колебаний:

s(t) = A_n sin (2πf_nt+φ_n),                         (1.1.2)

или непосредственно функцией s(t) = y(t ± kT_p), k = 1,2,3,..., где Т_р – период одного полного колебания сигнала y(t), заданного на одном периоде. Значение f_p =1/T_p называют фундаментальной частотой колебаний. Полигармонические сигналы представляют собой сумму определенной постоянной составляющей (f_о=0) и произвольного (в пределе – бесконечного) числа гармонических составляющих с произвольными значениями амплитуд A_n и фаз j_n, с периодами, кратными периоду фундаментальной частоты f_p. Другими словами, на периоде фундаментальной частоты f_p, которая равна или кратно меньше минимальной частоты гармоник, укладывается кратное число периодов всех гармоник, что и создает периодичность повторения сигнала. Частотный спектр полигармонических сигналов дискретен, в связи с чем второе распространенное математическое представление сигналов - в виде спектров (рядов Фурье).

В качестве примера на рис. 1.1.6 приведен отрезок периодической сигнальной функции, которая получена суммированием постоянной составляющей (частота постоянной составляющей равна 0) и трех гармонических колебаний с разными значениями частоты и начальной фазы колебаний. Математическое описание сигнала задается формулой:

s(t) = A_k×cos(2×π×f_k×t+φ_k),

где: A_k = {5, 3, 4, 7} – амплитуда гармоник; f_k = {0, 40, 80, 120} – частота в герцах;
 φ_k = {0, -0.4, -0.6, -0.8} – начальный фазовый угол колебаний в радианах; k = 0, 1, 2, 3. Фундаментальная частота сигнала 40 Гц. Частотное представление данного сигнала (спектр сигнала) приведено на рисунке 1.

 

Рисунок 1 – Модель и спектр сигнала.

Периодический сигнал любой произвольной формы может быть представлен в виде суммы гармонических колебаний с частотами, кратными фундаментальной частоте колебаний f_р= 1/Т_р. Для этого достаточно разложить один период сигнала в ряд Фурье по тригонометрическим функциям синуса и косинуса с шагом по частоте, равным фундаментальной частоте f = f_p:

s(t) = (a_k cos 2πkΔft + b_k sin 2πkΔft),

a_o = (1/T) s(t) dt,  a_k = (2/T) s(t) cos 2πkΔft dt,

b_k = (2/T) s(t) sin 2πkΔft dt.  

Количество членов ряда Фурье K = k_max обычно ограничивается максимальными частотами f_max гармонических составляющих в сигналах так, чтобы f_max < K·f_p. Однако для сигналов с разрывами и скачками имеет место f_max ® ¥ , при этом количество членов ряда ограничивается по допустимой погрешности аппроксимации функции s(t).

Одночастотные косинусные и синусные гармоники можно объединить и представить разложение в более компактной форме:

s(t) = S_k cos (2πkΔft-φ_k),

S_k = 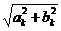, φ_k = argtg (b_k/a_k).

Рисунок 2 – Прямоугольный периодический сигнал (меандр)

Пример представления прямоугольного периодического сигнала (меандра) в виде амплитудного ряда Фурье в частотной области приведен на рисунке 2. Сигнал четный относительно t=0, не имеет синусных гармоник, все значения φ_k для данной модели сигнала равны нулю.

К непериодическим сигналам относят почти периодические и апериодические сигналы. Основным инструментом их анализа также является частотное представление.

Рисунок 3 – Почти периодический сигнал и спектр его амплитуд

Почти периодические сигналы близки по своей форме к полигармоническим. Они также представляют собой сумму двух и более гармонических сигналов (в пределе – до бесконечности), но не с кратными, а с произвольными частотами, отношения которых (хотя бы двух частот минимум) не относятся к рациональным числам, вследствие чего фундаментальный период суммарных колебаний бесконечно велик. Как правило, почти периодические сигналы порождаются физическими процессами, не связанными между собой. Математическое отображение сигналов тождественно полигармоническим сигналам (сумма гармоник), а частотный спектр также дискретен.

Апериодические сигналы составляют основную группу непериодических сигналов и задаются произвольными функциями времени. На рисунке 4 показан пример апериодического сигнала, заданного формулой на интервале (0, ¥):

s(t) = exp(-a×t) - exp(-b×t),

где a и b – константы, в данном случае a = 0.15, b = 0.17. 

Рисунок 4 –  Апериодический и импульсный сигналы и модуль их спектра

Частотный спектр апериодических сигналов непрерывен и может содержать любые гармоники в частотном интервале [0, ¥]. Для его вычисления используется интегральное преобразование Фурье, которое можно получить переходом от суммирования к интегрированию при
Δf ® 0 и kΔf ® f.

s(t) = (a(f) cos 2πft + b(f) sin 2πft) df = S(f) cos(2πft-φ(f)) df.

a(f) = s(t) cos 2πft dt, b(f) = s(t) sin 2πft dt,

S(f) = , φ(f) = argtg (b(f)/a(f)).

Частотные функции a(f), b(f) и S(f) представляют собой не амплитудные значения соответствующих гармоник на определенных частотах, а распределения спектральной плотности амплитуд этих гармоник по частотной шкале.  Эти формулы обычно называют формулами прямого и обратного преобразования Фурье.

Теорема Парсеваля. Полная энергия спектра сигнала:

                                     E_s = W(f) df = |S(f)|² df.

Так как координатное и частотное представление по существу только разные математические отображения одного и того же сигнала, то равной должна быть и энергия сигнала в двух представлениях, откуда следует равенство Парсеваля:

|s(t)|² dt = |S(f)|² df,

т.е. энергия сигнала равна интегралу модуля его частотного спектра – сумме энергий всех частотных составляющих сигнала. Аналогично для энергии взаимодействия сигналов:

x(t) y*(t) dt = X(f) Y*(f) df.

Из равенства Парсеваля следует инвариантность скалярного произведения сигналов и нормы относительно преобразования Фурье:

(x(t),y(t)) = (X(f),Y(f)), ||x(t)||² = ||X(f)||².

Не следует забывать, что при представлении спектров в круговых частотах (по ω) в правой части приведенных равенств должен стоять множитель 1/2π.

 

Спектр частотно-модулированного сигнала. В общем виде найти этот спектр трудно. Однако для практики это и не нужно. Достаточно знать:

а) что при частотной модуляции спектр информационного сигнала  переносится на несущую частоту ;

б) практическую ширину спектра ЧМ-сигнала .

Установлено, что практическая ширина спектра ЧМ-сигнала определяется выражением:

= ,

где  – коэффициент, или индекс частотной модуляции;  – девиация частоты .

При  имеем широкополоснуюЧМ. Тогда

При  имеем узкополосную ЧМ.

 

 

Принимаемый сигнал – как случайный процесс; виды случайных процессов, законы и числовые характеристики; корреляционные характеристики и свойства процессов; преобразования Винера-Хинчина; белый шум

 

Случайный процесс Х(t) представляет собой функцию, которая отличается тем, что принимаемые ею значения в любые произвольные моменты времени по координате t являются случайными. Строго с теоретических позиций, случайный процесс X(t) следует рассматривать как совокупность временных функций x_k(t), имеющих определенную общую статистическую закономерность. При регистрации случайного процесса на определенном временном интервале осуществляется фиксирование единичной реализации x_k(t) из бесчисленного числа возможных реализаций процесса X(t). Эта единичная реализация называется выборочной функцией случайного процесса X(t). Примеры выборочных функций модельного случайного процесса X(t) приведены на рисунке 5. В дальнейшем без дополнительных пояснений при рассмотрении различных параметров и характеристик случайных процессов для сопровождающих примеров будем использовать данную модель процесса.

Рисунок 5 – Выборочные функции случайного процесса

С практической точки зрения выборочная функция является результатом отдельного эксперимента, после которого данную реализацию x_k(t) можно считать детерминированной функцией. Сам случайный процесс в целом должен анализироваться с позиции бесконечной совокупности таких реализаций, образующих статистический ансамбль. Полной статистической характеристикой такой системы является N-мерная плотность вероятностей р(x_n;t_n). Однако, как экспериментальное определение N-мерных плотностей вероятностей процессов, так и их использование в математическом анализе представляет значительные математические трудности. Поэтому на практике обычно ограничиваются одно- и двумерной плотностью вероятностей процессов.

 

Функциональные характеристики случайного процесса. Допустим, что случайный процесс X(t) задан ансамблем реализаций {x₁(t), x₂(t),… x_k(t),…}. В произвольный момент времени t₁ зафиксируем зафиксируем значения всех реализаций {x₁(t₁), x₂(t₁),… x_k(t₁),…}. Совокупность этих значений представляет собой случайную величину X(t₁) и является одномерным сечением случайного процесса X(t). Примеры сечений по 100 выборкам случайного процесса X(t) в точках t₁ и t₂ (рисунок 5) приведены на рисунке 6. Случайные процессы и их функции характеризуются неслучайными функциями математического ожидания (среднего значения), дисперсии и корреляции:

Рисунок 6 – Сечения случайного процесса X(t)

Математическое ожидание(mean value) представляет собой статистическое усреднение случайной величины X(t_i), под которым понимают усреднение по ансамблю реализаций в каком либо фиксированном сечении t_i случайного процесса. Соответственно, функция математического ожидания является теоретической оценкой среднего взвешенного значения случайного процесса по временной оси:

m_x(t) º M{Х(t)}º = x p(x;t) dx,

Математическое ожидание m_x(t) представляет собой неслучайную составляющую случайного процесса X(t). На рисунка 5 и 6 неслучайные составляющие m(t) модели случайного процесса X(t) выделены пунктиром и соответствуют выборкам N ® ¥.

Функция дисперсии (variance) случайного процесса является теоретической оценкой среднего взвешенного значения разности Х(t)-m_x(t), которая называется флюктуационной частьюпроцесса:

D_x(t) = M{[Х(t)-m_x(t)]²} = M{X²(t)} - m_x²(t) = [x_o(t)]² p(x;t) dx,

x_o(t) = x(t)-m_x(t).

Функция среднего квадратического отклонения (standard deviation) служит амплитудной мерой разброса значений случайного процесса по временной оси относительно математического ожидания процесса:

σ_x(t) = .

Рисунок 7

Учитывая последнее выражение, дисперсия случайной величины обычно обозначается индексом σ_x². На рисунке 7 приведен пример флюктуационной составляющей процесса X(t) (рисунок 5) в одной из реализаций в сопоставлении со средним квадратическим отклонением ±σ случайных величин от математического ожидания m(t).

 

Классификация случайных процессов. Случайные процессы различают по степени однородности их протекания во времени (по аргументу).

Нестационарные процессы. В общем случае значения функций математического ожидания, дисперсии и корреляции могут быть зависимыми от момента времени t, т.е. изменяться во времени. Такие процессы составляют класс нестационарных процессов.

Стационарные процессы.Процесс называют стационарным, если плотность вероятностей процесса не зависит от начала отсчета времени и если на интервале его существования выполняются условия постоянства математического ожидания и дисперсии, а корреляционная функция является функцией только разности аргументов τ = t₂-t₁, т.e.:

m_Х(t₁) = m_Х(t₂) = m_Х = const,

D_Х(t₁) = D_Х(t₂) = D_Х = const,

R_Х(t₁,t₁+τ) º R_x(t₂-τ,t₂) = R_Х(τ) º R_Х(-τ),

r_x(τ) = R_x(τ)/D_x, r_x(0) = 1, |r_x(τ)| ≤ 1, r_x(-τ) = r_x(τ).

Последние выражения свидетельствует о четности корреляционной (а равно и ковариационной) функции и функции корреляционных коэффициентов. Из него вытекает также еще одно свойство смешанных моментов стационарных процессов:

|R_x(τ)| £ R_x(0),  |K_x(τ)| £ K_x(0) º D_x.

Чем медленнее по мере увеличения значений τ убывают функции R_x(τ) и r_x(τ), тем больше эффективный интервал корреляции случайного процесса, и тем медленнее изменяются во времени его реализации.

Среди стационарных процессов выделяют строго стационарные процессы, для которых постоянны во времени не только математическое ожидание, дисперсия и корреляция, но и все остальные моменты высших порядков (в частности, асимметрия и эксцесс).

Стационарные случайные процессы наиболее часто встречаются при решении физических и технических задач. Теория стационарных случайных функций разработана наиболее полно и для ее использования обычно достаточно определения стационарности в широком смысле: случайная функция считается стационарной, если ее математическое ожидание постоянно, а корреляционная функция зависит только от одного аргумента. Случайные процессы, удовлетворяющие условиям стационарности на ограниченных, интересующих нас интервалах, также обычно относят к числу стационарных в широком смысле и называют квазистационарными.

 

 

Взаимно-корреляционная функция. Корреляция (correlation), и ее частный случай для центрированных сигналов – ковариация, является методом анализа сигналов. Приведем один из вариантов использования метода. Допустим, что имеется сигнал s(t), в котором может быть (а может и не быть) некоторая последовательность x(t) конечной длины Т, временное положение которой нас интересует. Для поиска этой последовательности в скользящем по сигналу s(t) временном окне длиной Т вычисляются скалярные произведения сигналов s(t) и x(t). Тем самым мы "прикладываем" искомый сигнал x(t) к сигналу s(t), скользя по его аргументу, и по величине скалярного произведения оцениваем степень сходства сигналов в точках сравнения.

Корреляционный анализ дает возможность установить в сигналах (или в рядах цифровых данных сигналов) наличие определенной связи изменения значений сигналов по независимой переменной, то есть, когда большие значения одного сигнала (относительно средних значений сигнала) связаны с большими значениями другого сигнала (положительная корреляция), или, наоборот, малые значения одного сигнала связаны с большими значениями другого (отрицательная корреляция), или данные двух сигналов никак не связаны (нулевая корреляция).

Корреляционные функции случайных процессов. Одномерные законы плотности распределения вероятностей случайных процессов не несут каких-либо характеристик связи между значениями случайных величин для различных значений аргументов.

Двумерная плотность вероятностей p(x₁,x₂; t₁,t₂) определяет вероятность совместной реализации значений случайных величин Х(t₁) и Х(t₂) в произвольные моменты времени t₁ и t₂ и в какой-то мере уже позволяет оценивать динамику развития процесса. Двумерная плотность вероятностей описывает двумерную случайную величину {X(t_i), X(t_j)} в виде функции вероятности реализации случайной величины X(t_i) в бесконечно малом интервале dx_i в окрестностях x_i в момент времени t_i при условии, что в момент времени t_j значение X(t_j) будет реализовано в бесконечно малом интервале dx_j в окрестностях x_j:

p(x_i,x_j; t_i,t_j) dx_i dx_j = P{|X(t_i-x_i|≤dx_i/2, |X(t_j-x_j|≤dx_j/2}.

Характеристикой динамики изменения двумерной случайной величины {X(t_i), X(t_j)} является корреляционная функция, которая описывает случайный процесс в целом:

R_X(t_i,t_j) = M{X(t₁) X(t₂)}.

Корреляционная функция представляет собой статистически усредненное произведение значений случайного процесса X(t) в моменты времени t_i и t_j по всем значениям временных осей t_i и t_j, а следовательно тоже является двумерной функцией. В терминах теории вероятностей корреляционная функция является вторым начальным моментом случайного процесса.

На рисунке 8 приведены примеры реализаций двух случайных процессов, которые характеризуются одной и той же функцией математического ожидания и дисперсии.

Рисунок 8

На рисунке видно, что хотя пространство состояний обоих процессов практически одно и то же, динамика развития процессов в реализациях существенно различается. Единичные реализации коррелированных процессов в произвольный момент времени могут быть такими же случайными, как и некоррелированных, а в пределе, во всех сечениях оба процесса могут иметь один и тот же закон распределения случайных величин. Однако динамика развития по координате t (или любой другой независимой переменной) единичной реализации коррелированного процесса по сравнению с некоррелированным является более плавной, а, следовательно, в коррелированном процессе имеется определенная связь между последовательными значениями случайных величин. Оценка степени статистической зависимости мгновенных значений какого-либо процесса Х(t) в произвольные моменты времени t₁ и t₂ и производится функцией корреляции. По всему пространству значений случайного процесса X(t) корреляционная функция определяется выражением:

R_Х(t_i,t_j) = x(t_i)x(t_j) p(x_i,t_j; x_i,t_j) dx_i dx_j,

Рисунок 10 – Двумерная плотность вероятностей и корреляционная функция процесса X(t)

На рисунке 10 приведена форма модельного случайного процесса X(t) в одной выборке со значительной и изменяющейся неслучайной составляющей. Модель задана на интервале 0-Т (Т=100) в дискретной форме с шагом Δt=1. Корреляционная функция вычислена по заданной плотности вероятностей модели

При анализе случайных процессов второй момент времени t_j удобно задавать величиной сдвига τ относительно первого момента, который при этом может быть задан в виде координатной переменной:

R_Х(t,t+τ) = M{Х(t)Х(t+τ)}.

Функция, задаваемая этим выражением, обычно называется автокорреляционной функцией случайного процесса.

Белый шумявляется стационарным случайным процессом x(t) с постоянной спектральной плотностью G_x(f) = σ², равной дисперсии значений x(t). Другими словами, все спектральные составляющие белого шума имеют одинаковую энергию (как белый цвет содержит все цвета видимого спектра).

По своему физическому смыслу спектральная плотность – это мощность процесса, которая приходится на 1 Гц полосы частот. Но тогда идеального белого шума на практике не может существовать, так как для него должно было бы выполняться условие:

R_x(0) = G_x(f) df = (σ²/2)×δ(0) = ¥,

т.е. мощность белого шума и его дисперсия равны бесконечности, а значения шума не коррелированны для любых |τ| ¹ 0, так как корреляционная функция представляет собой идеальный дельта-импульс. Тем не менее многие помехи в радиотехнике, в технике связи и в других отраслях рассматривают как белый шум, если выполняется соотношение между шириной спектров полезных сигналов и шумов B_{k сигнал}/B_k.шум << 1, и спектральная плотность шумов слабо изменяется в интервале спектра сигнала.

Рисунок 11 – Функции корреляции белого шума в частотном интервале 0-В.

Если частотный диапазон спектра, на котором рассматриваются сигналы и помехи, равен
0-В, то спектральная плотность шума задается в виде:

G_x(f) = σ², 0 £ f £ B; G_x(f) = 0, f > B.

При этом корреляционная функция шума определяется выражением:

R_x(τ) = σ²B×sin(2πBτ) / 2πBτ.

Эффективная шумовая ширина спектра:

B_k = R_x(0)/G_x(f)_max = B.

Эффективное шумовое время ковариации:

T_k = 2 |R_x(τ)|dτ /R_x(0).

Реальное шумовое время ковариации целесообразно определить по ширине главного максимума функции R_x(τ), в котором сосредоточена основная часть энергии шумов, при этом
T_k = 1/В и B_kT_k = 1, т.е. соотношение неопределенности выполняется.

Как следует из всех этих выражений и наглядно видно на рисунке, при ограничении частотного диапазона в шумах появляется определенная ковариация между значениями и чем меньше частотный диапазон шумов, тем больше их радиус ковариации. По существу, ограничение частотного диапазона шумов определенным диапазоном эквивалентно фильтрации белого шума частотным фильтром с соответствующей шириной полосы пропускания, при этом корреляционная функция импульсного отклика фильтра переносится на шум.

Теорема Хинчина-Колмогорова (также известная как Теорема Винера-Хинчина и иногда как Теорема Винера-Хинчина-Эйнштейна) утверждает, что спектральной плотностью мощности стационарного в широком смысле случайного процесса является преобразование Фурье соответствующей автокорреляционной функции.

Непрерывный случай:

где  есть автокорреляционная функция, определённая через математическое ожидание, и где  – спектральная плотность мощности функции . Отметим, что автокорреляционная функция определена через математическое ожидание от произведения и что преобразования Фурье от не существует в общем случае, так как стационарные случайные функции не инегрируемы в квадратичном. Звёздочка означает комплексное сопряжение, оно может быть опущено, если случайный процесс вещественный.

Дискретный случай:

где  и где  – спектральная плотность мощности с дискретными значениями . Являясь упорядоченной по дискретным отсчётам времени, спектральная плотность – периодическая функция в частотной области.

Теорема удобна для анализа линейных стационарных систем, где входные и выходные значения не интегрируемы в квадратичном, из-за чего преобразований Фурье не существует. Как следствие, преобразование Фурье автокорреляционной функции выходного сигнала системы равно произведению преобразования Фурье автокорреляционной функции входного сигнала системы на квадрат модуля преобразования Фурье её импульсной характеристики. Это выполняется даже когда преобразований Фурье входных и выходных сигналов не существует, из-за того что они не интегрируемы. Поэтому входные и выходные параметры не могут быть прямо связаны преобразованием Фурье импульсной передаточной функции.

Из того, что преобразование Фурье автокорреляционной функции сингала есть спектр мощности сигнала, следует, что спектр мощности выходного сигнала равен произведению спектра мощности входного и передаточной функции системы. Это следствие используется в нахождении спектра мощности параметрическим методом.

 

Векторное представление сигнала; дискретизация сигнала по времени; теорема отсчетов (Котельникова); дискретизация по уровню, шум квантования; условие ретрансляции; понятие ИКМ и ДМ сигнала

Дискретизация сигналов. Под дискретизацией сигналов понимают преобразование функций непрерывных переменных в функции дискретных переменных, по которым исходные непрерывные функции могут быть восстановлены с заданной точностью. Роль дискретных отсчетов выполняют, как правило, квантованные значения функций в дискретной шкале координат. Под квантованием понимают преобразование непрерывной по значениям величины в величину с дискретной шкалой значений из конечного множества разрешенных, которые называют уровнями квантования. Если уровни квантования нумерованы, то результатом преобразования является число, которое может быть выражено в любой числовой системе. Округление с определенной разрядностью мгновенных значений непрерывной аналоговой величины с равномерным шагом по аргументу является простейшим случаем дискретизации и квантования сигналов при их преобразовании в цифровые сигналы.

Принципы дискретизации. Сущность дискретизации аналоговых сигналов заключается в том, что непрерывность во времени аналоговой функции s(t) заменяется последовательностью коротких импульсов, амплитудные значения которых c_n определяются с помощью весовых функций, либо непосредственно выборками (отсчетами) мгновенных значений сигнала s(t) в моменты времени t_n.Представление сигнала s(t) на интервале Т совокупностью дискретных значений c_n записывается в виде:

(с₁, с₂, ... , c_N) = А[s(t)],

где А - оператор дискретизации. Запись операции восстановления сигнала s(t):

s'(t) = В[(с₁, с₂, ... , c_N)].

Выбор операторов А и В определяется требуемой точностью восстановления сигнала. Наиболее простыми являются линейные операторы. В общем случае:

с_n = q_n(t) s(t) dt,

где q_n(t) – система весовых функций.

Отсчеты в этом выражении связаны с операцией интегрирования, что обеспечивает высокую помехоустойчивость дискретизации. Однако в силу сложности технической реализации "взвешенного" интегрирования, последнее используется достаточно редко, при высоких уровнях помех. Более широкое распространение получили методы, при которых сигнал s(t) заменяется совокупностью его мгновенных значений s(t_n) в моменты времени t_n. Роль весовых функций в этом случае выполняют гребневые (решетчатые) функции. Отрезок времени Δt между соседними отсчетами называют шагом дискретизации. Дискретизация называется равномерной с частотой F=1/Δt, если значение Δt постоянно по всему диапазону преобразования сигнала. При неравномерной дискретизации значение Δt между выборками может изменяться по определенной программе или в зависимости от изменения каких-либо параметров сигнала.

Воспроизведение непрерывного сигнала по выборкам может проводиться как на основе ортогональных, так и неортогональных базисных функций. Воспроизводящая функция s'(t) соответственно представляется аппроксимирующим полиномом:

s'(t) = c_n v_n(t),

где v_n(t) - система базисных функций. Ортогональные базисные функции обеспечивают сходимость ряда к s(t) при n Þ ¥. Оптимальными являются методы дискретизации, обеспечивающие минимальный числовой ряд при заданной погрешности воспроизведения сигнала. При неортогональных базисных функциях используются, в основном, степенные алгебраические полиномы вида:

                                                           s'(t) = c_n tⁿ.

Если значения аппроксимирующего полинома совпадают со значениями выборок в моменты их отсчета, то такой полином называют интерполирующим. В качестве интерполирующих полиномов обычно используются многочлены Лагранжа. Для реализации интерполирующих полиномов необходима задержка сигнала на интервал дискретизации, что в системах реального времени требует определенных технических решений. В качестве экстраполирующих полиномов используют, как правило, многочлены Тейлора.

Естественным требованием к выбору частоты дискретизации является внесение минимальных искажений в динамику изменения сигнальных функций. Логично полагать, что искажения информации будут тем меньше, чем выше частота дискретизации F. С другой стороны также очевидно, что чем больше значение F, тем большим количеством цифровых данных будут отображаться сигналы, и тем большее время будет затрачиваться на их обработку. В оптимальном варианте значение частоты дискретизации сигнала F должно быть необходимым и достаточным для обработки информационного сигнала с заданной точностью, т.е. обеспечивающим допустимую погрешность восстановления аналоговой формы сигнала (среднеквадратическую в целом по интервалу сигнала, либо по максимальным отклонениям от истинной формы в характерных информационных точках сигналов).

Интерполяционный ряд Котельникова-Шеннона. Допустим, что для обработки задается произвольный аналоговый сигнал s(t), имеющий конечный и достаточно компактный фурье-образ S(f). Равномерная дискретизация непрерывного сигнала s(t) с частотой F (шаг Δt = 1/F) с математических позиций означает умножение функции s(t) на гребневую функцию
Ш_Δt(t) = δ(t-kΔt) – непрерывную последовательность импульсов Кронекера:

s_Δt(t) = s(t)×Ш_Δt(t) = s(t) 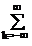δ(t-kΔt) = 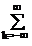s(kΔt)δ(t-kΔt).

С учетом известного преобразования Фурье гребневой функции 

Ш_Δt(t) Û (1/T) δ(f-nF) = F·Ш_F(f),

фурье-образ дискретной функции s_Δt(t):

S_F(f) = S(f) _* F×Ш_F(f).

Отсюда, для спектра дискретного сигнала имеем:

S_F(f) = F×S(f) 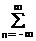_* δ(f-n_F) = F 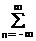S(f-n_F).

Спектр дискретизированного сигнала представляет собой сумму сдвинутых копий исходного аналогового сигнала с шагом сдвига, равным частоте дискретизации. Очевидно, что если спектры копий не перекрываются, то по центральной копии дискретного спектра можно восстановить исходный аналоговый сигнал с абсолютной точностью. Умножая функцию на прямоугольную весовую функцию П_F(f), равную 1 в пределах главного частотного диапазона
[-F/2,F/2] и нулю за его пределами, получаем непрерывный спектр в бесконечных по частоте границах, равный спектру F×S(f) в пределах главного частотного диапазона:

F×S(f) = F×[S(f) _* Ш_F(f)]×П_F(f).

Обратное преобразование Фурье такого спектра должно давать конечный и непрерывный сигнал. Произведем обратное преобразование обеих частей равенства:

F·[S(f) _* Ш_F(f)] Û s_Δt(t), П_F(f) Û F×sinc(πFt).

F×s(t) = s_Δt(t) _* F×sinc(πFt).

s(t) = sinc(πFt) 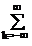_* s(kΔt)δ(t-kΔt),

Дискретизированный сигнал s_Δt(t) = s(kΔt)δ(t-kΔt)  представляет собой сумму последовательных весовых импульсов Кронекера, сдвинутых на интервал Δt, со значениями веса, равными значениям отсчетов функции s(t) в моменты kΔt. При прохождении такого сигнала через систему с импульсным откликом h(t)= sinc(πFt)= sin(πFt)/πFt каждый весовой импульс Кронекера возбудит на выходе соответствующую последовательную серию сдвинутых и масштабированных копий оператора фильтра. Отсюда, с учетом очевидного равенства

δ(t-kΔt) _* sinc(πFt) = sinc[πF(t-kΔt)],

выходной сигнал будет представлять собой сумму сдвинутых весовых импульсных откликов системы, где значение веса определяется отсчетами дискретного сигнала:

s(t) = 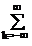s(kΔt) sinc[πF(t-kΔt)] = 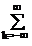s(kΔt) sinc[π(t/Δt-k)].

Эта конечная формула носит название интерполяционного ряда Котельникова-Шеннона. Из нее следует, что если наибольшая частота в спектре произвольной непрерывной функции s(t) не превышает частоты ее дискретизации, то она без потери точности может быть представлена в виде числовой последовательности дискретных значений s(kt), k = 0,1,2,... , и однозначно восстановлена по этой последовательности. В этом и состоит сущность теоремы отсчетов Котельникова. В зарубежной литературе она называется также теоремой Шеннона или теоремой дискретизации (sampling teorem).

Дискретизация с усреднением.Если дискретизация сигнала производится импульсами конечной ширины, то таким импульсам соответствуют средние значения сигнала на интервале длительности импульсов. При дискретизации с усреднением спектр S(f) заменяется спектром периодическое продолжение которого и образует спектр дискретной функции. При обратном преобразовании Фурье и при использовании интерполяционной формулы Котельникова-Шеннона, вместо исходной функции s(t) получаем функцию s'(t) = s(t) _* П_r(t)/r, что эквивалентно пропусканию сигнала через фильтр с откликом h(t) = П_r(t)/r, т.е. через низкочастотный сглаживающий фильтр "скользящего" среднего с окном r.

Шум квантования — шум, появляющийся в результате дискретизации непрерывного сигнала. Шум квантования оказывает на процесс передачи информации по существу такое же влияние, как и помехи в канале связи.

Импульсно-кодовая модуляция (ИКМ, англ. Pulse Code Modulation, PCM) используется для оцифровки аналоговых сигналов. Практически все виды аналоговых данных (видео, голос, музыка, данные телеметрии, виртуальные миры) допускают применение PCM. Чтобы получить на входе канала связи (передающий конец) ИКМ-сигнал из аналогового, мгновенное значение аналогового сигнала измеряется через равные промежутки времени. Количество оцифрованных значений в секунду (или скорость оцифровки, частота дискретизации) должно быть не ниже 2-кратной максимальной частоты в спектре аналогового сигнала (по теореме Котельникова). Мгновенное измеренное значение аналогового сигнала округляется до ближайшего уровня из нескольких заранее определённых значений. Этот процесс называется квантованием, а количество уровней всегда берётся кратным степени двойки, например, 8, 16, 32 или 64. Номер уровня может быть соответственно представлен 3, 4, 5 или 6 битами. Таким образом, на выходе модулятора получается набор битов (0 и 1).

Демодуляция. На приёмном конце канала связи демодулятор преобразует последовательность битов в импульсы собственным генератором с тем же уровнем квантования, который использовал модулятор. Далее эти импульсы используются для восстановления аналогового сигнала в ЦАП.

Дельта-модуляция сигнала. Сигналы от измерительных датчиков и любых других источников информации передаются по линиям связи к приемникам – измерительным приборам, в измерительно-вычислительные системы регистрации и обработки данных, в любые другие центры накопления и хранения данных. Как правило, информационные сигналы являются низкочастотными и ограниченными по ширине спектра, в отличие от широкополосных высокочастотных каналов связи, рассчитанных на передачу сигналов от множества источников одновременно с частотным разделением каналов. Перенос спектра сигналов из низкочастотной области в выделенную для их передачи область высоких частот выполняется операцией модуляции.

Допустим, что низкочастотный сигнал, подлежащий передаче по какому-либо каналу связи, задается функцией s(t). В канале связи для передачи данного сигнала выделяется определенный диапазон высоких частот. На входе канала связи в специальном передающем устройстве формируется вспомогательный, как правило, непрерывный во времени периодический высокочастотный сигнал u(t) = f(t; a₁, a₂, … a_m). Совокупность параметров a_i определяет форму вспомогательного сигнала. Значения параметров a_i в отсутствие модуляции являются величинами постоянными. Если на один из этих параметров перенести сигнал s(t), т.е. сделать его значение пропорционально зависимым от значения s(t) во времени (или по любой другой независимой переменной), то форма сигнала u(t) приобретает новое свойство. Она несет информацию, тождественную информации в сигнале s(t). Именно поэтому сигнал u(t) называют несущим сигналом, несущим колебанием или просто несущей (carrier), а физический процесс переноса информации на параметры несущего сигнала – его модуляцией (modulation). Исходный информационный сигнал s(t) называют модулирующим (modulating signal), результат модуляции – модулированным сигналом (modulated signal). Обратную операцию выделения модулирующего сигнала из модулированного колебания называют демодуляцией (demodulation).

Эффективным способом преобразования сигналов в цифровую форму является дельта-модуляция. В каждый момент отсчёта сигнал сравнивается с пилообразным напряжением на каждом шаге дискретизации d. Если отсчёт сигнала превышает по амплитуде пилообразное напряжение, то последнее нарастает до следующей точки дискретизации, в противном случае оно спадает. В простейшей системе наклон пилообразного напряжения сохраняется неизменным на всём протяжении процесса. Полученный бинарный сигнал можно рассматривать как производную от пилообразного напряжения. Выбирая достаточно малым значение шага d , можно получить любую заданную точность представления сигнала. Преимущество дельта-модуляции по сравнению, например, с ИКМ, которая также образует бинарный сигнал, заключается не столько в реализуемой точности при заданной частоте дискретизации, сколько в простоте реализации.

 

Понятие информации; понятие энтропии, избыточности; оценка энтропии дискретного и непрерывного источника; энтропия шумового сигнала

В теории информации и передачи сигналов под информацией понимают совокупность сведений о каких-либо событиях, процессах, явлениях и т.п., рассматриваемых в аспекте их передачи в пространстве и во времени. Информацию передают в виде сообщений. Сообщением называют информацию, выраженную в определенной форме и предназначенную для передачи от источника к адресату. Примерами сообщений служат тексты телеграмм, речь, музыка, телевизионное изображение, данные на выходе компьютера, команды в системе автоматического управления объектами и т.п. Сообщения передают с помощью сигналов, которые являются носителями информации. Основным видом сигналов являются электрические сигналы. В последнее время всё большее распространение получают оптические сигналы, например, в волоконно-оптических линиях передачи информации.

 

Энтропия – это количество информации, приходящейся на одно элементарное сообщение источника, вырабатывающего статистически независимые сообщения.

Информационная энтропия для независимых случайных событий x с n возможными состояниями (от 1 до n) рассчитывается по формуле:

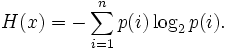
Эта величина также называется средней энтропией сообщения. Величина называется частной энтропией, характеризующей только i-e состояние.

Таким образом, энтропия события x является суммой с противоположным знаком всех произведений относительных частот появления события i, умноженных на их же двоичные логарифмы (основание 2 выбрано только для удобства работы с информацией, представленной в двоичной форме). Это определение для дискретных случайных событий можно расширить для функции распределения вероятностей.

Энтропия является количеством, определённым в контексте вероятностной модели для источника данных. Например, кидание монеты имеет энтропию − 2(0,5log₂0,5) = 1 бит на одно кидание (при условии его независимости). У источника, который генерирует строку, состоящую только из букв «А», энтропия равна нулю: . Так, например, опытным путём можно установить, что энтропия английского текста равна 1,5 бит на символ, что конечно будет варьироваться для разных текстов. Степень энтропии источника данных означает среднее число битов на элемент данных, требуемых для её зашифровки без потери информации, при оптимальном кодировании. Некоторые биты данных могут не нести информации. Например, структуры данных часто хранят избыточную информацию, или имеют идентичные секции независимо от информации в структуре данных. Количество энтропии не всегда выражается целым числом бит.

Математические свойства энтропии:

1. Неотрицательность: .
2. Ограниченность: . Равенство, если все элементы из X равновероятны.
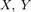3. Если независимы, то .
4. Энтропия — выпуклая вверх функция распределения вероятностей элементов.
5. Если 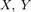имеют одинаковое распределение вероятностей элементов, то H(X) = H(Y).

 

Избыточность — термин из теории информации, означающий превышение количества информации, используемой для передачи или хранения сообщения, над его информационной энтропией. Для уменьшения избыточности применяется сжатие данных без потерь, в то же время контрольная сумма применяется для внесения дополнительной избыточности в поток, что позволяет производить исправление ошибок при передаче информации по каналам, вносящим искажения (спутниковая трансляция, беспроводная передача и т. д.).

Информационное содержание одного сообщения в потоке, в наиболее общем случае, определяется как:

Обозначим как R логарифм числа символов в алфавите сообщений: R = log | M |

Абсолютная избыточность может быть определена как разность этих двух величин:

D = R − r

Соотношение D/R называется относительной избыточностью и дает математическую оценку максимальной степени сжатия, на которую может быть уменьшен размер файла.

Энтропия дискретного источника.Шеннон предположил, что прирост информации равен утраченной неопределённости, и задал требования к её измерению:

ü мера должна быть непрерывной; то есть изменение значения величины вероятности на малую величину должно вызывать малое результирующее изменение функции;

ü в случае, когда все варианты (буквы в приведённом примере) равновероятны, увеличение количества вариантов (букв) должно всегда увеличивать значение функции;

ü должна быть возможность сделать выбор (в нашем примере букв) в два шага, в которых значение функции конечного результата должно являться суммой функций промежуточных результатов.

Поэтому функция энтропии H должна удовлетворяет условиям:

1. определена и непрерывна для всех , где для всех и . (Нетрудно видеть, что эта функция зависит только от распределения вероятностей, но не от алфавита.)
2. Для целых положительных n, должно выполняться следующее неравенство:

1. Для целых положительных b_i, где , должно выполняться равенство:

Шеннон показал, что единственная функция, удовлетворяющая этим требованиям, имеет вид:  где K — константа (и в действительности нужна только для выбора единиц измерения).

Шеннон определил, что измерение энтропии ( ), применяемое к источнику информации, может определить требования к минимальной пропускной способности канала, требуемой для надёжной передачи информации в виде закодированных двоичных чисел. Для вывода формулы Шеннона необходимо вычислить математическое ожидание «количества информации», содержащегося в цифре из источника информации. Мера энтропии Шеннона выражает неуверенность реализации случайной переменной. Таким образом, энтропия является разницей между информацией, содержащейся в сообщении, и той частью информации, которая точно известна (или хорошо предсказуема) в сообщении. Примером этого является избыточность языка — имеются явные статистические закономерности в появлении букв, пар последовательных букв, троек и т. д. (см. цепи Маркова).

Определение энтропии Шеннона связано с понятием термодинамической энтропии. Больцман и Гиббс проделали большую работу по статистической термодинамике, которая способствовала принятию слова «энтропия» в информационную теорию. Существует связь между термодинамической и информационной энтропией. Например, демон Максвелла также противопоставляет термодинамическую энтропию информации, и получение какого-либо количества информации равно потерянной энтропии.

 

Энтропия непрерывного источника. В одном отсчете любого непрерывного сообщения содержится бесконечное количество собственной информации. И тем не менее, непрерывные сообщения (телефонные разговоры, телепередачи) успешно передаются по каналам связи. Это объясняется тем, что на практике никогда не требуется абсолютно точного воспроизведения переданного сообщения, а для передачи даже с очень высокой, но ограниченной точностью, требуется конечное количество информации, также как и при передаче дискретных сообщений. Данное обстоятельство и положено в основу определения количественной меры собственной информации, источников непрерывных сообщений. В качестве такой меры, принимается минимальное количество информации, необходимое для воспроизведения непрерывного сообщения с заданной точностью. Очевидно, что при таком подходе собственная информация зависит не только от свойств источника сообщений, но и от выбора параметра e, характеризующего точность воспроизведения. Возможны различные подходы к определению e в зависимости от вида и назначения передаваемой информации. Наиболее часто в информационной технике в качестве e используют среднеквадратическое отклонение между принятым у и переданным х сигналами, отражающими непрерывные сообщения, т.е.

	,
где Х и Y – ансамбли сигналов, отражающих исходное и воспроизведенное сообщения. Два варианта сообщения или сигнала, различающиеся не более, чем на заданное значение e0, называются эквивалентными. Взаимная информация I(X,Y) между двумя эквивалентными процессами X(t) и Y(t) может быть определена как I(X,Y)=h(X)-h(X/Y),

где h(X) и h(X/Y) – соответственно дифференциальная и условная дифференциальная энтропии.

Из приведенного выражения видно, что величина I(X,Y) зависит не только от собственного распределения w(х) ансамбля Х, но и от условного распределения w(x/y), которое определяется способом преобразования процесса X в Y. Для характеристики собственной информации, содержащейся в одном отсчете процесса Х, нужно устранить ее зависимость от способа преобразования сообщения Х в эквивалентное ему сообщение Y. Этого можно добиться, если под количеством собственной информации или e - энтропией He(Х) процесса Х понимать минимизированную по всем распределениям w(X/Y) величину I(X,Y), при которой сообщения Х и Y еще эквивалентны, т.е.

.

Таким образом, e - энтропия определяет минимальное количество информации, содержащейся в одном отсчете непрерывного сообщения, необходимое для воспроизведения его с заданной верностью.

 

Информационная характеристика сигнала: скорость передачи сигнала; бод, скорость передачи сигнала; пропускная способность дискретного сигнала в канале с помехами; пропускная способность канала с шумовой помехой; теорема Шеннона; согласование канала с сигналом

 

Канал связи– это совокупность средств, предназначенных для передачи сигналов (сообщений). Существуют различные типы каналов, которые можно классифицировать по различным признакам:

По типу линий связи:проводные; кабельные; оптико-волоконные; линии электропередачи; радиоканалы и т.д.

По характеру сигналов:непрерывные; дискретные; дискретно-непрерывные (сигналы на входе системы дискретные, а на выходе непрерывные, и наоборот).

По помехозащищенности:каналы без помех; с помехами.

Каналы связи характеризуются:

1. Емкость каналаопределяется как произведениевремени использования канала T_к, ширины спектра частот, пропускаемых каналом F_к и динамического диапазона D_к., который характеризует способность канала передавать различные уровни сигналов.V_к = T_к F_к D_к.

Условие согласования сигнала с каналом: V_c £ V_k;T_c £ T_k;F_c £ F_k;V_c £ V_k;D_c £ D_k.

2.Скорость передачи информации – среднее количество информации, передаваемое в единицу времени.

3. Пропускная способность канала связи – наибольшая теоретически достижимая скорость передачи информации при условии, что погрешность не превосходит заданной величины.

4. Количество информации и избыточность.

Дискретные системы связи – системы, в которых как реализации сообщения, так и реализации сигнала представляют собой последовательности символов алфавита, содержащего конечное число элементарных символов. 

Единицей измерения количества информации является бит, который представляет собой количество информации, получаемое при наблюдении случайной величины, имеющей два равновероятных значения.

При равномерном распределении  количество информации задается формулой Хартли:

.

Справедливы следующие соотношения:

1)

2)

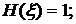
3)  если  и  - независимы.

Избыточность– обеспечивает достоверность передаваемой информации (R = 0¸1).

Одной из задач теории информации является определение зависимости скорости передачи информации и пропускной способности канала связи от параметров канала и

Скорость передачи данных в значительной мере зависит от передающей среды в каналах связи, в качестве которых используются различные типы линий связи:

Проводные:

1. Витая пара (что частично подавляет электромагнитное излучение других источников). Скорость передачи до 1 Мбит/с. Используется в телефонных сетях и для передачи данных.

2. Коаксиальный кабель.Скорость передачи 10–100 Мбит/с – используется в локальных сетях, кабельном телевидении и т.д.

3.Оптико-волоконная.Скорость передачи 1 Гбит/с.

В средах 1–3 затухание в дБ линейно зависит от расстояния, т.е. мощность падает по экспоненте. Поэтому через определенное расстояние нужно ставить ретрансляторы (усилители).

Радиолинии:

1. Радиоканал.Скорость передачи 100–400 Кбит/с. Использует радиочастоты до 1000 МГц. До 30 МГц за счет отражения от ионосферы возможно распространение электромагнитных волн за пределы прямой видимости. Но этот диапазон сильно зашумлен (например, любительской радиосвязью). От 30 до 1000 МГц – ионосфера прозрачна и необходима прямая видимость. Антенны устанавливаются на высоте (иногда устанавливаются регенераторы). Используются в радио и телевидении.

2. Микроволновые линии.Скорости передачи до 1 Гбит/с. Используют радиочастоты выше 1000 МГц. При этом необходима прямая видимость и остронаправленные параболические антенны. Расстояние между регенераторами 10–200 км. Используются для телефонной связи, телевидения и передачи данных.

3. Спутниковая связь. Используются микроволновые частоты, а спутник служит регенератором (причем для многих станций). Характеристики те же, что у микроволновых линий.

 

Бод (англ. baud) в связи и электронике – единица измерения символьной скорости, количество изменений информационного параметра несущего периодического сигнала в секунду. Названа по имени Эмиля Бодо, изобретателя кода Бодо – кодировки символов для телетайпов.

Зачастую, ошибочно, считают, что бод – это количество бит, переданное в секунду. В действительности же это верно лишь для двоичного кодирования, которое используется не всегда. Например, в современных модемах используется квадратурная амплитудная модуляция (КАМ), и одним изменением уровня сигнала может кодироваться несколько (до 16) бит информации. Например, при символьной скорости 2400 бод скорость передачи может составлять 9600 бит/c благодаря тому, что в каждом временном интервале передаётся 4 бита.

Кроме этого, бодами выражают полную ёмкость канала, включая служебные символы (биты), если они есть. Эффективная же скорость канала выражается другими единицами, например битами в секунду (бит/c, bps).

 

Дисктретные системы передачи информации. Условной энтропией величины  при наблюдении величины  называется

Справедливы соотношения:

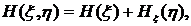
Взаимной информацией величин  и  называется

Справедливы следующие соотношения:

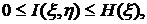
Если  и независимы, то =0.

При расчетах условной энтропии и взаимной информации удобно пользоваться следующими соотношениями теории вероятностей:

1) теорема умножения вероятностей ;

2) формула полной вероятности

3) формула Байеса

Теорема Шеннона для дискретного канала: Если поток информации, вырабатываемый источником, достаточно близок к пропускной способности канала связи, т.е. , где – сколь угодно малая величина, то всегда можно найти такой способ кодирования, который обеспечит передачу всех сообщений источника, причем скорость передачи информации будет весьма близкой к пропускной способности канала.

 

Непрерывные системы передачи информации.      Пусть  – реализации непрерывного сообщения на входе какого-либо блока схемы связи,  – реализация выходного сообщения (сигнала),  – одномерная плотность вероятности ансамбля входных сообщений,  – одномерная плотность вероятности ансамбля выходных сообщений, 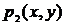 – совместная плотность вероятности,  – условная плотность вероятности при известном  Тогда для количества информации  справедливы следующие соотношения:

,

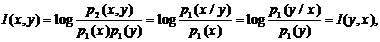
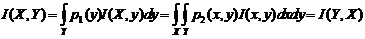Здесь  – взаимная информация между каким-либо значением входного и значением выходного сообщений,  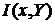– средние значения условной информации,  – полная средняя взаимная информация. Условная энтропия определяется по формуле:         

 

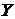Когда  и  статистически связаны между собой, то

При независимых  и

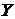
Полная средняя взаимная информация определяется формулой:

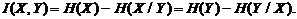
Теорема Шеннона для непрерывного канала с шумом. Если энтропия источника непрерывных сообщений сколь угодно близка к пропускной способности канала, то существует метод передачи, при котором все сообщения источника будут переданы со сколь угодно высокой верностью воспроизведения.

 

Дискретный канал связи с помехами

Каналом без памяти называется канал, в котором на каждый передаваемый символ сигнала, помехи воздействуют, не зависимо от того, какие сигналы передавались ранее. То есть помехи не создают дополнительные коррелятивные связи между символами. Название «без памяти» означает, что при очередной передаче канал как бы не помнит результатов предыдущих передач. При наличии помехи среднее количество информации в принятом символе сообщении – Y, относительно переданного – X равно:

Для символа сообщения X_T длительности T, состоящегоиз n элементарных символов среднее количество информации в принятом символе сообщении – Y_T относительно переданного – X_T равно: I(Y_T, X_T) = H(X_T) – H(X_T/Y_T) = H(Y_T) – H(Y_T/X_T) = n [H(Y) – H (Y/X)

Для определения потерь в дискретном канале связи используется канальная матрица (матрица переходных вероятностей), позволяющая определить условную энтропию характеризующую потерю информации на символ сообщения. Скорость передачи информации по дискретному каналу с помехами равна:

Пропускная способность дискретного канала при наличии помех равна максимально допустимой скорости передачи информации, причем максимум разыскивается по всем распределениям вероятностей p(x) на X и, поскольку, энтропия максимальна для равномерного распределения (для равновероятных символов сообщения), то выражение для пропускной способности имеет вид:

.

Как видно из формулы, наличие помех уменьшает пропускную способность канала связи.

Основная теорема Шеннона о кодировании для дискретного канала с помехами: Для дискретного канала с помехами существует такой способ кодирования, который позволяет осуществлять безошибочную передачу информации, если производительность источника ниже пропускной способности

 

Согласование сигнала с каналом. Канал связи можно характеризовать так же, как и сигнал, тремя параметрами: временем Т_К, в течение которого по каналу ведется передача; полосой пропускания канала F_K и динамическим диапазоном D_K. Под динамическим диапазоном канала понимают отношение допустимой мощности передаваемого сигнала к мощности помехи, неизбежно присутствующей в канале. Типы каналов, по которым передаются сообщения, многочисленны и разнообразны. Широко применяются каналы проводной связи, коротковолновой радиосвязи с использованием отражения от ионосферы, ультракоротковолновой связи ионосферного и тропосферного рассеяния, метеорной связи, космической связи и т. п. Характеристики этих каналов значительно отличаются друг от друга. Обобщенной характеристикой непрерывного канала является его емкость (объем): VK = Т_К * F_K * D_K.

Необходимым условием неискаженной передачи по каналу сигналов с объемом VС должно быть V_C<V_K. Для согласования сигнала с каналом осуществляют вторичное преобразование первичного сигнала. В простейшем случае сигнал согласуют с каналом по всем трем параметрам, т.е. добиваются выполнения условий: Т_С<Т_К; F_C<F_K; D_C<D_K.

При этих условиях объем сигнала полностью «вписывается» в объем канала. Однако первое неравенство может выполняться и тогда, когда не выполнены одно или два из вторых неравенств. Это означает, что можно производить «обмен» длительности на ширину спектра или ширину спектра на динамический диапазон и т.д. Например, записанный на пленку сигнал можно воспроизводить с пониженной скоростью. При этом диапазон частот исходного сигнала уменьшится во столько раз, во сколько увеличится время передачи. Принятый сигнал также записывается на пленку, а затем воспроизводится с повышенной скоростью для восстановления исходного сигнала. Записанный сигнал можно передавать также и с повышенной скоростью. Широко используется также обмен динамического диапазона на полосу пропускания. Так, использование помехоустойчивых широкополосных видов модуляции позволяет передать сообщение по каналам с увеличенным уровнем помех. Но это требует полосы пропускания канала более широкой, чем спектр сообщения.

 

---

Дата добавления: 2018-02-15; просмотров: 1207; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

1234Следующая ⇒

---

Мы поможем в написании ваших работ!