Критерий Вальда (минимаксный или максиминный критерий)
Применение данного критерия не требует знания вероятностей состояний  . Этот критерий опирается на принцип наибольшей осторожности, поскольку он основывается на выборе наилучшей из наихудшей стратегий
. Этот критерий опирается на принцип наибольшей осторожности, поскольку он основывается на выборе наилучшей из наихудшей стратегий  .
.
Если в исходной матрице (по условию задачи) результат  представляет потери ЛПР, то при выборе оптимальной стратегии используется минимаксный критерий. Для определения оптимальной стратегии
представляет потери ЛПР, то при выборе оптимальной стратегии используется минимаксный критерий. Для определения оптимальной стратегии  необходимо в каждой строке матрицы результатов найти наибольший элемент
необходимо в каждой строке матрицы результатов найти наибольший элемент  , а затем выбирается действие
, а затем выбирается действие  (строка j), которому будет соответствовать наименьший элемент из этих наибольших элементов, т.е. действие, определяющее результат, равный
(строка j), которому будет соответствовать наименьший элемент из этих наибольших элементов, т.е. действие, определяющее результат, равный
 . (4.8)
. (4.8)
Если в исходной матрице по условию задачи результат  представляет выигрыш (полезность) лица, принимающего решение, то при выборе оптимальной стратегии используется максиминный критерий.
представляет выигрыш (полезность) лица, принимающего решение, то при выборе оптимальной стратегии используется максиминный критерий.
Для определения оптимальной стратегии  в каждой строке матрицы результатов находят наименьший элемент
в каждой строке матрицы результатов находят наименьший элемент  , а затем выбирается действие
, а затем выбирается действие  (строка j), которому будут соответствовать наибольшие элементы из этих наименьших элементов, т.е. действие, определяющее результат, равный
(строка j), которому будут соответствовать наибольшие элементы из этих наименьших элементов, т.е. действие, определяющее результат, равный
 . (4.9)
. (4.9)
Пример 4.2. Рассмотрим пример 4.1. Так как  в этом примере представляет потери (затраты), применим минимаксный критерий. Необходимые результаты вычисления приведены в следующей таблице:
в этом примере представляет потери (затраты), применим минимаксный критерий. Необходимые результаты вычисления приведены в следующей таблице:
|
|
|
| Состояния Стратегия | Затраты, д.е. ( |
|
| |||
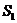
| 
| 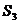
| 
| |||

| 6 | 12 | 20 | 24 | 24 | - |

| 9 | 7 | 9 | 28 | 28 | - |
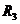
| 23 | 18 | 15 | 19 | 23 | 23 |

| 27 | 24 | 21 | 15 | 27 | - |
Таким образом, наилучшей стратегией развития провозных возможностей в соответствии с минимаксным критерием "лучший из худших" будет третья, т.е. 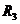 .
.
Минимаксный критерий Вальда иногда приводит к нелогичным выводам из-за своей чрезмерной "пессимистичности". "Пессимистичность" этого критерия исправляет критерий Сэвиджа.
Критерий Сэвиджа
Этот критерий использует матрицу рисков || 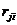 ||. Элементы данной матрицы можно определить по формулам (4.2) и (4.3), которые перепишем в следующем виде:
||. Элементы данной матрицы можно определить по формулам (4.2) и (4.3), которые перепишем в следующем виде:
 (4.10)
(4.10)
Это означает, что 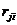 есть разница между наилучшим значением в столбце i и значениями и значениями
есть разница между наилучшим значением в столбце i и значениями и значениями  при том же i. Отметим, что независимо от того, является ли
при том же i. Отметим, что независимо от того, является ли  доходом (выигрышем) или потерями (затратами),
доходом (выигрышем) или потерями (затратами), 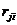 в обоих случаях определяет величины потерь ЛПР. Следовательно, можно применять к
в обоих случаях определяет величины потерь ЛПР. Следовательно, можно применять к 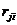 только минимаксный критерий. Критерий Сэвиджа рекомендует в условиях неопределенности выбирать ту стратегию
только минимаксный критерий. Критерий Сэвиджа рекомендует в условиях неопределенности выбирать ту стратегию  , при которой величина риска принимает наименьшее значение в самой неблагоприятной ситуации (когда риск максимален).
, при которой величина риска принимает наименьшее значение в самой неблагоприятной ситуации (когда риск максимален).
|
|
|
Пример 4.3. Рассмотрим пример 4.1. Заданная матрица определяет потери (затраты). По формуле (4.9) вычислим элементы матрицы рисков || 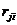 ||:
||:
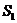
| 
| 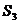
| 
| ||

| 0 | 5 | 11 | 9 | |
||  ||= ||=
| 
| 3 | 0 | 0 | 13 |
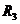
| 17 | 11 | 6 | 4 | |

| 21 | 17 | 12 | 0 |
Полученные результаты вычислений с использованием критерия минимального риска Сэвиджа оформим в следующей таблице:
| Состояние Стратегия | Величина риска, д.е. ( |
|
| |||
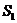
| 
| 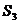
| 
| |||

| 0 | 5 | 11 | 9 | 11 | 11 |

| 3 | 0 | 0 | 13 | 13 | - |
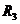
| 17 | 11 | 6 | 4 | 17 | - |

| 24 | 17 | 12 | 0 | 24 | - |
Введение величины риска 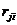 привело к выбору первой стратегии
привело к выбору первой стратегии  , обеспечивающей наименьшие потери (затраты) в самой неблагоприятной ситуации (когда риск максимален).
, обеспечивающей наименьшие потери (затраты) в самой неблагоприятной ситуации (когда риск максимален).
Применение критерия Сэвиджа позволяет любыми путями избежать большого риска при выборе стратегии, а, значит, избежать большего проигрыша (потерь).
Критерий Гурвица
Этот критерий основан на следующих двух предположениях: "природа" может находиться в самом невыгодном состоянии с вероятностью  и в самом выгодном состоянии с вероятностью
и в самом выгодном состоянии с вероятностью  , где
, где  - коэффициент доверия. Если результат
- коэффициент доверия. Если результат  - прибыль, полезность, доход и т.п., то критерий Гурвица записывается так:
- прибыль, полезность, доход и т.п., то критерий Гурвица записывается так:
|
|
|
 (4.11)
(4.11)
Когда  представляет затраты (потери), то выбирают действие, дающее
представляет затраты (потери), то выбирают действие, дающее
 (4.12)
(4.12)
Если  , получим пессимистичный критерий Вальда.
, получим пессимистичный критерий Вальда.
Если  , то приходим к решающему правилу вида
, то приходим к решающему правилу вида  или к так называемой стратегии "здорового оптимизма", т.е. критерий слишком оптимистичный.
или к так называемой стратегии "здорового оптимизма", т.е. критерий слишком оптимистичный.
Критерий Гурвица устанавливает баланс между случаями крайнего пессимизма и крайнего оптимизма путем взвешивания обоих способов проведения соответствующими весами  и
и  , где
, где  . Значение
. Значение  от 0 до 1 может определяться в зависимости от склонности ЛПР к пессимизму или к оптимизму. При отсутствии ярко выраженной склонности
от 0 до 1 может определяться в зависимости от склонности ЛПР к пессимизму или к оптимизму. При отсутствии ярко выраженной склонности  представляется наиболее разумной.
представляется наиболее разумной.
Пример 4.4. Критерий Гурвица используем в примере 4.1. Положим  . Результаты необходимых вычислений приведены ниже:
. Результаты необходимых вычислений приведены ниже:
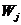
| 
| 
| 
| 
|
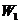
| 6 | 24 | 15 | 15 |
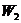
| 7 | 28 | 17,5 | - |
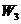
| 15 | 23 | 19 | - |

| 15 | 27 | 21 | - |
Оптимальное решение заключается в выборе W.
Таким образом, в примере предстоит сделать выбор, какое из возможных решений предпочтительнее:
|
|
|
− по критерию Лапласа - выбор стратегии  ;
;
− по критерию Вальда - выбор стратегии 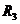 ;
;
− по критерию Сэвиджа - выбор стратегии  ;
;
− по критерию Гурвица при  - выбор стратегии
- выбор стратегии  , а если ЛПР - пессимист (
, а если ЛПР - пессимист (  ), то выбор стратегии
), то выбор стратегии 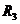 .
.
Это определяется выбором соответствующего критерия (Лапласа, Вальда, Сэвиджа или Гурвица).
Выбор критерия принятия решений в условиях неопределенности является наиболее сложным и ответственным этапом. При этом не существует каких-либо общих советов или рекомендаций. Выбор критерия должно производить ЛПР с учетом конкретной специфики решаемой задачи и в соответствии со своими целями, а также опираясь на прошлый опыт и собственную интуицию.
В частности, если даже минимальный риск недопустим, то следует применять критерий Вальда. Если, наоборот, определенный риск вполне приемлем и ЛПР намерено вложить в некоторое предприятие столько средств, чтобы потом оно не сожалело, что вложено слишком мало, то выбирают критерий Сэвиджа.
ТЕОРИЯ ИГР
В отличие от рассмотренных выше задач принятия решений в условиях определенности, риска и неопределенности, в которых внешняя среда (природа) предполагалась пассивной, в конфликтных ситуациях имеются противодействующие стороны, интересы которых противоположны. При конфликтных ситуациях решения принимаются в условиях неопределенности двумя и более разумными противниками, каждый из которых стремится оптимизировать свои решения за счет других. Теория, занимающаяся принятием решений в условиях конфликтных ситуаций, называется теорией игр. Математическая модель конфликтной ситуации представляет собой игру.
Игра - это совокупность правил, описывающих сущность конфликтной ситуации. Эти правила устанавливают:
- выбор образа действия игроков на каждом этапе игры;
- информацию, которой обладает каждый игрок при осуществлении таких выборов;
- плату для каждого игрока после завершения любого этапа игры.
Игру можно определить следующим образом:
- имеются n конфликтующих сторон (игроков), принимающих решения, интересы которых не совпадают;
- сформулированы правила выбора допустимых стратегий, известные игрокам;
- определен выбор возможных конечных состояний игры (например, выигрыш, ничья, проигрыш);
- всем игрокам (участникам игры) заранее известны платежи, соответствующие каждому возможному конечному состоянию. Платежи задаются в виде матрицы  .
.
В зависимости от числа конфликтующих сторон игры делятся на парные (с двумя игроками) и множественные (имеющие не менее трех игроков). Каждый игрок имеет некоторое множество (конечное или бесконечное) возможных выборов, т.е. стратегий.
Стратегией игры называется совокупность правил, определяющих поведение игрока от начала игры до ее завершения. Стратегии каждого игрока определяют результаты или платежи в игре. Игра называется игрой с нулевой суммой, если проигрыш одного игрока равен выигрышу другого, в противном случае она называется игрой с ненулевой суммой.
В данном разделе рассматриваются только игры двух лиц с нулевой суммой. Задание стратегий (А и В) двух игроков в парной игре полностью определяет ее исход, т.е. выигрыш одного или проигрыш другого. Игра называется конечной, если у каждого игрока имеется конечное число стратегий. Результаты конечной парной игры с нулевой суммой можно задавать матрицей, строки и столбцы которой соответствуют различным стратегиям, а ее элементы - выигрышам одной стороны (равные проигрышам другой). Эта матрица называется платежной матрицей или матрицей игры.
Если первый игрок имеет m стратегий, а второй - n стратегий, то говорят, что мы имеем дело с игрой 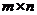 . Пусть заданы множество стратегий: для первого игрока
. Пусть заданы множество стратегий: для первого игрока  , для второго игрока
, для второго игрока 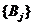 , платежная матрица
, платежная матрица 
 , где
, где 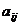 - выигрыш первого игрока или проигрыш второго игрока при выборе ими стратегий
- выигрыш первого игрока или проигрыш второго игрока при выборе ими стратегий  и
и 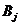 соответственно. Каждый из игроков выбирает однозначно с вероятностью 1 некоторую стратегию, т.е. пользуется при выборе решения чистой стратегией. При этом решение игры будет в чистых стратегиях. Поскольку интересы игроков противоположны, то первый игрок стремится максимизировать свой выигрыш, а второй игрок, наоборот, минимизировать свой проигрыш.
соответственно. Каждый из игроков выбирает однозначно с вероятностью 1 некоторую стратегию, т.е. пользуется при выборе решения чистой стратегией. При этом решение игры будет в чистых стратегиях. Поскольку интересы игроков противоположны, то первый игрок стремится максимизировать свой выигрыш, а второй игрок, наоборот, минимизировать свой проигрыш.
Решение игры состоит в определении наилучшей стратегии каждым игроком. Выбор наилучшей стратегии одним игроком проводится при полном отсутствии информации о принимаемом решении вторым игроком. Следует отметить, что и первый, и второй игрок являются разумными противниками, которые находятся в состоянии конфликта. Поэтому для решения игры двух лиц с нулевой суммой используется очень "пессимистичный" критерий, так называемый критерий мини-макса-максимина. Этот критерий рассмотрен выше. Основное отличие заключается в том, что ранее "природа" не рассматривалась как активный противник, тогда как в теории игр каждый игрок действует разумно и, следовательно, пытается активно помешать своему противнику. Так, если первый игрок применяет стратегию  , то второй будет стремиться к тому, чтобы выбором соответствующей стратегии
, то второй будет стремиться к тому, чтобы выбором соответствующей стратегии 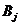 свести выигрыш первого игрока к минимуму, что равнозначно сведения своего проигрыша к минимуму. Величина этого минимума
свести выигрыш первого игрока к минимуму, что равнозначно сведения своего проигрыша к минимуму. Величина этого минимума
 ,
,  . (5.1)
. (5.1)
Первый игрок (при любых ответах противника) будет стремиться найти такую стратегию, при которой  обращается в максимум:
обращается в максимум:
 . (5.2)
. (5.2)
Величина  называется нижней ценой игры. Ей соответствует максиминная стратегия, придерживаясь которой первый игрок при любых стратегиях противника обеспечит себе выигрыш, не меньший
называется нижней ценой игры. Ей соответствует максиминная стратегия, придерживаясь которой первый игрок при любых стратегиях противника обеспечит себе выигрыш, не меньший  . Другими словами, нижняя цена игры является гарантированным выигрышем первого игрока при любых стратегиях второго игрока.
. Другими словами, нижняя цена игры является гарантированным выигрышем первого игрока при любых стратегиях второго игрока.
Аналогично определим по каждому столбцу матрицы 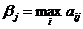 ,
,  , найдем минимальное значение
, найдем минимальное значение  :
:
 . (5.3)
. (5.3)
Величина 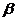 называется верхней ценой игры. Ей соответствует минимаксная стратегия второго игрока. Величина
называется верхней ценой игры. Ей соответствует минимаксная стратегия второго игрока. Величина 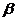 представляет собой гарантированный проигрыш второго игрока при любой стратегии первого игрока.
представляет собой гарантированный проигрыш второго игрока при любой стратегии первого игрока.
Пример 5.1. Дана платежная матрица  , которая определяет выигрыши игрока А. Вычислить нижнюю и верхнюю цены заданной игры.
, которая определяет выигрыши игрока А. Вычислить нижнюю и верхнюю цены заданной игры.
 .
.
Решение
Представим нашу игру в виде следующей таблицы:
| Стратегии первого игрока, | Стратегии второго игрока, | Значение, |
| |||

| 
| 
| 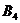
| |||

| 10 | 4 | 11 | 7 | 4 | - |

| 7 | 6 | 8 | 20 | 6 | 6 |

| 6 | 2 | 1 | 11 | 1 | - |
Значение 
| 10 | 6 | 11 | 20 | - | |
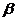
| - | 6 | - | - | - | - |
Если игрок А выбирает первую стратегию, он может получить выигрыш в размере 10, 4, 11 или 7 д.е. в зависимости от выбранной стратегии игроком В. При этом выигрыш игрока будет не меньше  д.е. независимо от поведения игрока В. Аналогично при выборе игроком А второй стратегии гарантированный выигрыш
д.е. независимо от поведения игрока В. Аналогично при выборе игроком А второй стратегии гарантированный выигрыш 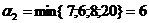 д.е. При выборе игроком А третьей стратегии выигрыш
д.е. При выборе игроком А третьей стратегии выигрыш  д.е.
д.е.
Таким образом, минимальные значения  ,
,  определяют минимально гарантированный выигрыш для игрока А, если он выбирает соответствующую стратегию i. Величина
определяют минимально гарантированный выигрыш для игрока А, если он выбирает соответствующую стратегию i. Величина 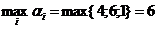 д.е. будет гарантированным выигрышем игрока А при любых стратегиях игрока В. Выбранная игроком А вторая стратегия называется максиминной стратегией, а соответствующее ее значение выигрыша
д.е. будет гарантированным выигрышем игрока А при любых стратегиях игрока В. Выбранная игроком А вторая стратегия называется максиминной стратегией, а соответствующее ее значение выигрыша  д.е. будет нижней ценой игры.
д.е. будет нижней ценой игры.
Второй игрок стремится минимизировать свой проигрыш. Выбрав первую стратегию  , игрок В может проиграть не более чем
, игрок В может проиграть не более чем  д.е. независимо от выбора стратегии игроком А. Аналогично рассуждая, получим следующие результаты (д.е.):
д.е. независимо от выбора стратегии игроком А. Аналогично рассуждая, получим следующие результаты (д.е.):
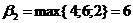 ;
; 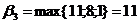 ;
;  .
.
Игрок В выбирает стратегию  , которая минимизирует его максимальные проигрыши:
, которая минимизирует его максимальные проигрыши:
 д.е.
д.е.
Величина 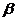 =6 д.е. будет гарантированным проигрышем игрока В при любых стратегиях игрока А. Выбранная игроком В вторая стратегия называется минимаксной стратегией, а соответствующее ее значение проигрыша
=6 д.е. будет гарантированным проигрышем игрока В при любых стратегиях игрока А. Выбранная игроком В вторая стратегия называется минимаксной стратегией, а соответствующее ее значение проигрыша  =6 д.е. будет верхней ценой игры.
=6 д.е. будет верхней ценой игры.
Следует отметить, что для любой матрицы  выполняется неравенство
выполняется неравенство
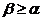 . (5.4)
. (5.4)
Если  , т.е. верхняя цена равна нижней цене игры, то соответствующие чистые стратегии называются оптимальными. А про игру говорят, что она имеет седловую точку. Седловая точка является минимальным элементом соответствующей строки и максимальным элементом соответствующего столбца. Эта точка есть точка равновесия игры, определяющая однозначно оптимальные стратегии. Оптимальность здесь означает, что ни один игрок не стремится изменить свою стратегию, так как его противник может на это ответить выбором другой стратегии, дающей худший для первого игрока результат.
, т.е. верхняя цена равна нижней цене игры, то соответствующие чистые стратегии называются оптимальными. А про игру говорят, что она имеет седловую точку. Седловая точка является минимальным элементом соответствующей строки и максимальным элементом соответствующего столбца. Эта точка есть точка равновесия игры, определяющая однозначно оптимальные стратегии. Оптимальность здесь означает, что ни один игрок не стремится изменить свою стратегию, так как его противник может на это ответить выбором другой стратегии, дающей худший для первого игрока результат.
Величина  называется ценой игры. Она определяет средней выигрыш игрока А и средний проигрыш игрока В при использовании ими оптимальных стратегий. В нашем примере цена игры
называется ценой игры. Она определяет средней выигрыш игрока А и средний проигрыш игрока В при использовании ими оптимальных стратегий. В нашем примере цена игры  д.е., оптимальная пара стратегий -
д.е., оптимальная пара стратегий -  и
и  .
.
Отдельные игры могут не иметь седловых точек, т.е. у каждого игрока не существует единственной, наиболее надежной стратегии. В этом случае используют смешанную стратегию. Смешанная стратегия состоит в том, что в ходе игры происходит случайный выбор стратегии из некоторого множества смешанных стратегий и для каждой смешанной стратегии указывается вероятность ее выбора. Смешанная стратегия для игрока А представляет собой вектор
 , (5.5)
, (5.5)
где  - вероятность выбора i-ой стратегии игроком и удовлетворяет следующим условиям:
- вероятность выбора i-ой стратегии игроком и удовлетворяет следующим условиям:
 ,
,  ;
;
 . (5.6)
. (5.6)
Аналогично смешанная стратегия игрока В представляет собой вектор
 , (5.7)
, (5.7)
где  - вероятность выбора j-ой стратегии игроком В - удовлетворяет следующим условиям:
- вероятность выбора j-ой стратегии игроком В - удовлетворяет следующим условиям:
 ,
,  ;
;
 . (5.8)
. (5.8)
Платежная матрица игры имеет следующий вид:
| В А | 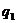
| 
| 
| … | 
| |

| 
| 
| 
| … | 
| |

| 
| 
| 
| … | 
| (5.9) |

| 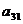
| 
| 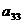
| … | 
| |
| … | … | … | … | … | … | |

| 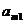
| 
| 
| … | 
|
Игрок А выбирает стратегию  так, чтобы максимизировать наименьший ожидаемый выигрыш по столбцам платежной матрицы, тогда как игрок В выбирает стратегию
так, чтобы максимизировать наименьший ожидаемый выигрыш по столбцам платежной матрицы, тогда как игрок В выбирает стратегию  с целью минимизировать наибольший ожидаемый проигрыш по строкам. Математически критерий минимакса при смешанных стратегиях может быть описан следующим образом. Игрок А выбирает стратегию
с целью минимизировать наибольший ожидаемый проигрыш по строкам. Математически критерий минимакса при смешанных стратегиях может быть описан следующим образом. Игрок А выбирает стратегию  , дающую
, дающую
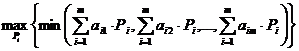 (5.10)
(5.10)
Игрок В выбирает стратегию  , дающую
, дающую
 (5.11)
(5.11)
Когда стратегии  и
и  оптимальны, то выполняется строгое равенство между максиминным ожидаемым выигрышем и минимаксным проигрышем, а результирующее значение равно оптимальному (ожидаемому) значению игры.
оптимальны, то выполняется строгое равенство между максиминным ожидаемым выигрышем и минимаксным проигрышем, а результирующее значение равно оптимальному (ожидаемому) значению игры.
Этот вывод следует из теоремы фон Неймана о минимаксе. Теорема утверждает, что выражения (5.10) и (5.11) имеют одно и то же значение  , называемое ценой игры. Если
, называемое ценой игры. Если  и
и  - оптимальные решения для обоих игроков, каждому элементу платежной матрицы
- оптимальные решения для обоих игроков, каждому элементу платежной матрицы  соответствует вероятность
соответствует вероятность  . Следовательно, оптимальное ожидаемое значение игры
. Следовательно, оптимальное ожидаемое значение игры
 . (5.12)
. (5.12)
Цена игры заключена между нижней и верхней ценами, т.е.
 .
.
Решить конечную игру – это значит нужно найти векторы Р и Q (оптимальные стратегии), удовлетворяющие теореме о минимаксе, а следовательно, получить величину ожидаемого платежа  - цену игры.
- цену игры.
Свойство оптимальности означает, что любое отступление одного из игроков от оптимальной стратегии (при условии, что второй игрок продолжает придерживаться своей оптимальной стратегии) при многократном повторении игры может только уменьшить его средний выигрыш (увеличить средний проигрыш).
Дата добавления: 2018-02-15; просмотров: 449; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!




