По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице.

Построена матрица парных коэффициентов корреляции

Свободный член уравнения в естественной форме равен … (Полученный ответ округлите до сотых.)

Решение:

Сначала найдем уравнение регрессии в стандартизированном виде. Будем считать х₁ – доход, х₂ – имущество. Коэффициенты парной корреляции известны и равны , , .
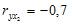Расчет стандартизированных коэффициентов выполним по формулам
= = 0,7236;
= = -0,4467.
Для построения уравнения в естественной форме воспользуемся формулой .

Итак, ;

По формуле рассчитаем свободный член уравнения в естественной форме.

= 3,7083 - 0,11 · 40 - ( -0,03)·48,0833=0,75.

3. В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х – объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам.

По данной выборке построено уравнение регрессии y = 3151,1 + 8,8487 · x. Коэффициент детерминации R² = 0,9708.

Средняя ошибка аппроксимации по уравнению регрессии, построенному по всей выборке, равна ____ %. (Полученное значение округлите до целых.) 36

Кейс 2 подзадача 1

Динамика показателя среднедушевого денежного дохода населения России в период 2005–2011 гг. характеризуется данными, представленными на графике.

Процесс построения функции тренда для временного ряда называется …

аналитическим выравниванием

Динамика показателя среднего размера назначенных пенсий в России в период 2005–2011 гг. характеризуется данными, представленными на графике.

Функция, описывающая зависимость между порядком коэффициента автокорреляции и его значением, называется …

автокорреляционной

Динамика показателя среднемесячной номинальной начисленной заработной платы работников организаций РФ в период 2005–2011 гг. характеризуется данными, представленными на графике.

Выявление структуры временного ряда возможно путем анализа значений …

автокорреляционной функции

Кейс 2 подзадача 2

Установите соответствие между порядком коэффициента автокорреляции и его значением.

1. Коэффициент автокорреляции первого порядка

2. Коэффициент автокорреляции второго порядка

3. Коэффициент автокорреляции третьего порядка

0,999097

0,998123

0,998261

Установите соответствие между порядком коэффициента автокорреляции и его значением.

1. Коэффициент автокорреляции первого порядка

2. Коэффициент автокорреляции второго порядка

3. Коэффициент автокорреляции третьего порядка

0,95603

0,97694

0,90784

Дата добавления: 2018-02-15; просмотров: 917; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 5 6 789 Следующая ⇒

Мы поможем в написании ваших работ!